皇后游戏——一道连洛谷题解都有错的题目
洛谷p2123
前言
这是一道省选/NOI-的题目,我认为这道题确实有这么难。很多人认为没有这么难,那是因为他们的做法并不是完全正确的。我看了洛谷仅有的三篇题解,竟然有两篇是有错的。正确的那篇题解在这里。这篇仅有的正解的作者还给出了一组证明另外几篇题解有误的数据,将在后面给出。
题目大意
有n个大臣,第i位大臣左手的数为 ai a i ,右手的数为 bi b i ,且 ai a i 和 bi b i 均为正整数。他能获得的数 ci c i 由以下关系给出:
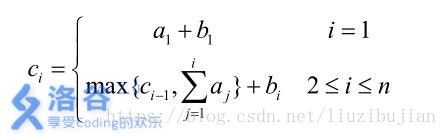
求 ci c i 最大的大臣的 ci c i 最小为多少。
题目思路
乍一看,这题和NOIP 2012 提高组 Day1 的国王游戏很像,做题方法应该也差不多,找出一个排序方法,使得以这样排序得到的序列会使最大的 ci c i 最小。观察可知, ci c i 是逐渐递增的。我们用相邻交换法考虑。设某个位置上的大臣编号为i,后面一位大臣的编号为j。设i前面所有大臣的a值之和为x,i前面那一位大臣的c值为y。若不交换,则c值较大的大臣的c值( cj c j )为
max(max(y,x+ai)+bi,x+ai+aj)+bj m a x ( m a x ( y , x + a i ) + b i , x + a i + a j ) + b j
化简后为
max(y+bi+bj,x+ai+bi+bj,x+ai+aj+bj m a x ( y + b i + b j , x + a i + b i + b j , x + a i + a j + b j )
同理,这两位大臣交换后,c值较大的大臣的c值( ci c i )为 max(y+bi+bj,x+aj+bi+bj,x+ai+aj+bi m a x ( y + b i + b j , x + a j + b i + b j , x + a i + a j + b i )
假设不交换更优,则有
max(y+bi+bj,x+ai+bi+bj,x+ai+aj+bj)≤max(y+bi+bj,x+ai+bi+bj,x+ai+aj+bj) m a x ( y + b i + b j , x + a i + b i + b j , x + a i + a j + b j ) ≤ m a x ( y + b i + b j , x + a i + b i + b j , x + a i + a j + b j )
发现两边都有 y+bi+bj y + b i + b j ,则可以消去,有:
max(x+ai+bi+bj,x+ai+aj+bj)≤max(x+ai+bi+bj,x+ai+aj+bj) m a x ( x + a i + b i + b j , x + a i + a j + b j ) ≤ m a x ( x + a i + b i + b j , x + a i + a j + b j )
然后可以把x消去:
max(ai+bi+bj,ai+aj+bj)≤max(ai+bi+bj,ai+aj+bj) m a x ( a i + b i + b j , a i + a j + b j ) ≤ m a x ( a i + b i + b j , a i + a j + b j ) ①
再进行化简:
max(bi,aj)+ai+bj≤max(bj,ai)+aj+bi m a x ( b i , a j ) + a i + b j ≤ m a x ( b j , a i ) + a j + b i ②
移项:
max(bi,aj)−aj−bi≤max(bj,ai)−ai−bj m a x ( b i , a j ) − a j − b i ≤ m a x ( b j , a i ) − a i − b j ③
观察左式, aj a j 和 bi b i 中大的数被消掉了,只剩下 aj a j 和 bi b i 中较小数的相反数,用数学语言表述出来就是 −min(aj,bi) − m i n ( a j , b i ) ,那么③式可以变成:
−min(aj,bi)≤−min(ai,bj) − m i n ( a j , b i ) ≤ − m i n ( a i , b j ) ④
再把负号处理掉:
min(ai,bj)≤min(aj,bi) m i n ( a i , b j ) ≤ m i n ( a j , b i ) ⑤
于是我们得到了一个非常简单的式子。
在洛谷AC但是错误的方法
根据得到的⑤式重载小于号(里面不能写小于等于,不然有几个点会RE,原因会在下面讲),然后进行排序。有了排完序的序列,后面只需要模拟求出每个数的c值就行了。
这是我的程序:
#include//不能写<=
}
}a[20005];
int t,n;
long long c[20005];
int main()
{
cin>>t;
for (int k=1;k<=t;k++)
{
cin>>n;
for (int i=1;i<=n;i++) cin>>a[i].x>>a[i].y;
sort(a+1,a+n+1);
long long s=0;
for (int i=1;i<=n;i++)
{
s+=a[i].x;
c[i]=max(c[i-1],s)+a[i].y;
}
cout<'\n';
}
} 其实不一定要用⑤式进行排序,按照上面的①②③④式进行排序都是可以的,只不过要注意开long long,因为数据很大,加法容易溢出。
这是我用②式写的程序:
#include20005];
int t,n;
long long c[20005];
int main()
{
cin>>t;
for (int k=1;k<=t;k++)
{
cin>>n;
for (int i=1;i<=n;i++) cin>>a[i].x>>a[i].y;
sort(a+1,a+n+1);
long long s=0;
for (int i=1;i<=n;i++)
{
s+=a[i].x;
c[i]=max(c[i-1],s)+a[i].y;
}
cout<'\n';
}
} 为什么重载小于号时不能加等号
我也是想了好久才想出来的。这其实是你快排没有掌握好,才会加等号。系统自带的排序和手写快排差不多,于是我手写了一下快排。
#include
i++;
}
while (a[j]>=x) j--;
if (i<=j)
{
int t=a[i];
a[i]=a[j];
a[j]=t;
i++;
j--;
}
}
if (lif (r>i) qsort(i,r);
}
int main()
{
cin>>n;
for (int i=1;i<=n;i++) cin>>a[i];
qsort(1,n);
for (int i=1;i<=n;i++) cout<' ';
} 重载小于号重载的就是第11行和16行的小于号,让我们看看改成小于等于号会有怎样的结果。你可以把注释掉的那行话的注释符取消掉,输出来。你会发现,它会循环到数组越界之后才会停止(本来开的100000的数组,等了好久才等到它输完,方便起见,改为1000)。所以重载小于号一定不能加等于,不然很容易RE。
为什么这种方法是错的
之前提到的三篇题解中唯一一篇正确的题解的作者提供了一组hack数据:
输入:
2
7
6 3
1 1
7 3
1 1
1 6
1 1
6 10
7
6 10
1 1
6 3
1 1
7 3
1 1
1 6输出:
26
26两组数据只是顺序不一样,但用上面的程序输出的结果也是不同的。为什么会这样呢?再具体地分析一下。假设有三位大臣,他们的a[i]和b[i]分别是:
7 3
1 1
1 6
显然,这样可以是排完序后的结果,因为两两之间用条件判断都是等于。这样算出来答案是17。而如果这样排:
1 1
1 6
7 3
答案是12,显然这样更优,但程序却有可能排成17的那种情况。
虽然按条件判断相等的两组数交换一次对后面确实不会产生影响,但可以通过多次交换对最终结果产生影响。
错误的根本原因就是,这个判断条件不满足传递性。
正确解法
写正确解法之前,我先要好好感谢一下那位第一个写正解的大佬,是他的博客和他的数据才引发了我以下的思考。
既然要使排序能满足传递性,就应该想出一个对所有数普遍适用的一个排序条件,而不只针对于相邻的两个数。上面得到的⑤式肯定要被用起来。再仔细观察一下这个式子:
min(ai,bj)≤min(aj,bi) m i n ( a i , b j ) ≤ m i n ( a j , b i )
可以发现,大概应该和a与b的大小关系有关( ai a i 和 bi b i 哪个大)。还有,要使一个数排在前面,那么a越小越好,b越大越好。我们先按a与b的大小关系把所有数据分为三大组,然后开始讨论:
1.当 ai<bi a i < b i , aj<bj a j < b j 时, ai≤aj a i ≤ a j ,应该按a升序排序( ai a i 和 aj a j 相等时无所谓)。
2.当 ai=bi a i = b i , aj=bj a j = b j 时,爱怎么排怎么排。
3.当 ai>bi a i > b i , aj>bj a j > b j 时, bi≥bj b i ≥ b j ,应该按b降序排序。
那么这三大组之间应该怎样排序呢?
1组和2组,1组在2组前肯定能保证满足条件。2组和3组,2组在3组前面肯定能保证满足条件。那么1组在前,2组在中,3组在后,是肯定能保证满足要求的。
我们令 di=ai−bi|ai−bi| d i = a i − b i | a i − b i | ,那么1组的d值为-1,2组为0,3组为1。
于是我们得到了最终的排序条件:先按d值排序;然后若d值小于等于0,按a升序排序(这里把2组归入1组);若d值大于0,则按b降序排序。
这样就可以满足传递性了。
这是完全正确的代码:
#includeif (d<=0) return xreturn y>a.y;
}
}a[20005];
int t,n;
long long c[20005];
int main()
{
cin>>t;
for (int k=1;k<=t;k++)
{
cin>>n;
for (int i=1;i<=n;i++)
{
cin>>a[i].x>>a[i].y;
if (a[i].x>a[i].y) a[i].d=1;
else if (a[i].x1;
else a[i].d=0;
}
sort(a+1,a+n+1);
long long s=0;
for (int i=1;i<=n;i++)
{
s+=a[i].x;
c[i]=max(c[i-1],s)+a[i].y;
}
cout<'\n';
}
} 总结
这一道题是一道不错的题,美中不足的是,数据太弱了,以致于让错误的解法鱼目混珠。这一道题对得起省选/NOI-的难度评定。希望下次来看的时候,数据已经加强了,正确的解法已经深入人心了。