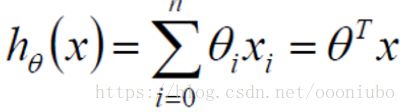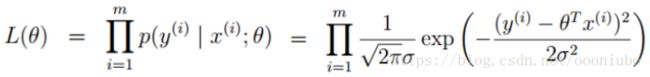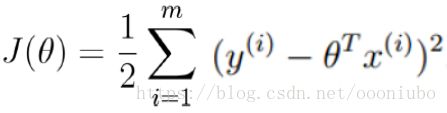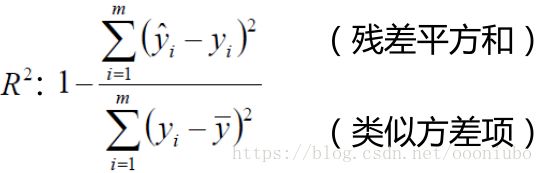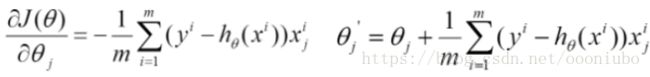人工智能-机器学习-监督学习-线性回归
回归算法是监督学习其中之一。
线性回归算法是已知样本和样本对应的预测结果，求新的样本的预测结果。
1、先对已知样本进行适当的处理，包括去除一些缺省值，一些不正常的值等。
2、样本和结果进行了建模，如下：
其中x为样本，h为y也为样本对应的值，
为系数，通过 可以很好拟合y，现在要求的就是。
后加入了非常非常关键的误差
，如下：
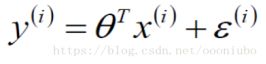
假设求的系数
为矩阵，含有很多的参数值，这是需要求解的。就是要求一个直线拟合所有的已知的样本和结果值。
其中x为样本属性，y为x对应的预测值，这两个值一直是已知了，比如x1，x2为工资和年龄，y为样本对应的银行给予的贷款值，
为误差，这个是关键突破点。
现在就是要通过x和y值求出来，使得x和y拟合最好。
3、关键点就是误差，误差
是一个1、独立。2、同分布。3、服从均值为0，方差为
，高斯分布，也就是正态分布。方差体现的是样本误差与误差均值的离散程度。
4、由于上面说到误差为高斯分布，所以如下：
这是概率密度函数。由2步骤得：
其实就是线性方程，解出来误差，带入到高斯分布的式子里面。
5、现在就要求，用参数估计的方法，求出值，现在根据样本估计参数方法求，方法是似然函数。
参数估计有点估计(point estimation)和区间估计(interval estimation)两种。
点估计是依据样本估计总体分布中所含的未知参数或未知参数的函数。通常它们是总体的某个特征值，如数学期望、方差和相关系数等。点估计问题就是要构造一个只依赖于样本的量，作为未知参数或未知参数的函数的估计值。例如，设一批产品的废品率为θ。为估计θ，从这批产品中随机地抽出n个作检查，以X记其中的废品个数，用X/n估计θ，这就是一个点估计。
最大似然估计：就是把我们观察到每个样本所对应的误差的概率乘到一起，然后试图调整参数以最大化这个概率的乘积，概率最大就是说明，误差最小，因为误差是在e的负指数，体现出来样本是符合这个概率分布，这样也是最佳参数，使得样本最佳拟合了这个分布最大。另外的解释，利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值。还有一种解释是，现在已经拿到了很多个样本（你的数据集中所有因变量），这些样本值已经实现，最大似然估计就是去找到那个（组）参数估计值，使得前面已经实现的样本值发生概率最大，这和回归的思路一样，线性回归是通过找到一个最好的参数，来最好的拟合样本和结果值，转化为最大似然估计是找到一组参数，使得样本发生的概率最大。
然后通过误差的密度函数高斯分布求出，自然函数：
求解出方法就是使得乘法化为加法，使用log，使得e指数为加法进行计算。
为了使得最大，就要使得后面的一项最小，所以单独提出后面一项。
这就是最小二乘法，这是通过最大似然估计法推出了最小二乘法。这就是目标函数。
6、对于最小二乘法，求最小值，也就是求极值，可以用导数方式，求其偏导，然后让偏导等于0，求出参数。
7，评估越接近1越好。其中分子为预测值和真实值差。这里说明下，评估方式有很多。都是为了评估模型的好坏。
8、梯度下降法，为什么引入，因为其实引入了目标函数后，怎么求解是最快，虽然是求偏导，但是不一定求出来，承接6步骤。所以这里引入了梯度下降法。
梯度下降法步骤：
1、找到下降的方向，梯度的反方向，梯度是上升的方向。
2、找到一小步，也有的可以先进行一大步，后面慢慢变小，这样可以提高速度，一般认为是目标函数对
的求导的值为单位的，有时候会求平均，有时候会求批量平均，有时候直接就认为是一小步的值。
3、迭代，每次对系数进行更新。
x和y都是确定了，对参数进行迭代，一直到目标函数最小时候，返回的值，就是所求的值。所以每次完成更新参数后，要带入目标函数进行求解，看是否最小，如果不是，就继续进行迭代，直到最小。初始值可以自己定义。m可以不必要全部进行迭代，可以选择64个样本进行迭代，当然如果内存高，不需要效率，只看结果，可以迭代更多的样本。
总结：
1、定义样本拟合的方程，参数有x，y，系数参数，误差。
2、误差为独立同分布的高斯分布，均值为0，方差为
，通过拟合方程，求出误差。
3、通过误差的特性，把2求的拟合方程带入高斯分布中，参数有x，y，，注意2中的均值和方差已经得到了。
3、通过点估计中的最大似然估计，转换求解拟合方程中的系数为求解样本最大分布的概率问题。最大似然估计用log求解，转换为最小二乘法。
4、梯度下降法，帮助快速求解最小二乘法。可以很好的迭代出来参数值得结果。
思路是比较简单，求解过程比思路相对来说多一些。