《动手学深度学习》task1——线性回归、softmax与分类模型,多层感知机笔记
系统学习《动手学深度学习》点击这里:
《动手学深度学习》task1_1 线性回归
《动手学深度学习》task1_2 Softmax与分类模型
《动手学深度学习》task1_3 多层感知机
《动手学深度学习》task2_1 文本预处理
《动手学深度学习》task2_2 语言模型
《动手学深度学习》task2_3 循环神经网络基础
本篇文章为task1中线性回归、softmax与分类模型,多层感知机的笔记
笔记目录
- 1 线性回归
- 1.1 pytorch语法
- 1.2 torch.matmul、mm和bmm的区别
- 1.3 nn.init 中实现参数的初始化函数
- 1.4 为何要引入激活函数
- 1.5 关于激活函数的选择
- 2 softmax回归
- 2.1 损失函数
- 2.2 交叉熵损失函数
- 2.3 定义损失函数:
- 2.4 画图
- 3 Pytorch定义模型
**系统学习《动手学深度学习》点击这里:**
《动手学深度学习》task1_1 线性回归
《动手学深度学习》task1_2 Softmax与分类模型
《动手学深度学习》task1_3 多层感知机
《动手学深度学习》task2_1 文本预处理
《动手学深度学习》task2_2 语言模型
《动手学深度学习》task2_3 循环神经网络基础
《动手学深度学习》task3_1 过拟合、欠拟合及其解决方案
《动手学深度学习》task3_2 梯度消失、梯度爆炸
《动手学深度学习》task3_3 循环神经网络进阶
《动手学深度学习》task4_1 机器翻译
《动手学深度学习》task4_2 注意力机制和Seq2seq模型
《动手学深度学习》task4_3 Transformer
《动手学深度学习》task5_1 卷积神经网络基础
《动手学深度学习》task5_2 LeNet
《动手学深度学习》task5_3 卷积神经网络进阶
《动手学深度学习》笔记:
《动手学深度学习》task1——线性回归、softmax与分类模型,多层感知机笔记
《动手学深度学习》task2——文本预处理,语言模型,循环神经网络基础笔记
《动手学深度学习》task3——过拟合、欠拟合及解决方案,梯度消失、梯度爆炸,循环神经网络进阶笔记
本篇目录
- 1 线性回归
- 1.1 pytorch语法
- 1.2 torch.matmul、mm和bmm的区别
- 1.3 nn.init 中实现参数的初始化函数
- 1.4 为何要引入激活函数
- 1.5 关于激活函数的选择
- 2 softmax回归
- 2.1 损失函数
- 2.2 交叉熵损失函数
- 2.3 定义损失函数:
- 2.4 画图
- 3 Pytorch定义模型
1 线性回归
1.1 pytorch语法
torch.mul(a, b)是矩阵a和b对应位相乘,a和b的维度必须相等,比如a的维度是(1, 2),b的维度是(1, 2),返回的仍是(1, 2)的矩阵
torch.mm(a, b)是矩阵a和b矩阵相乘,比如a的维度是(1, 2),b的维度是(2, 3),返回的就是(1, 3)的矩阵
torch.Tensor是一种包含单一数据类型元素的多维矩阵,定义了7种CPU tensor和8种GPU tensor类型。
torch.index_select(x, 1, indices)x为索引的对象,1表示维度,0为按行索引,1为按列索引,indices表示筛选的索引序号
torch.rand(*sizes, out=None) → Tensor 均匀分布
返回一个张量,包含了从区间[0, 1)的均匀分布中抽取的一组随机数。张量的形状由参数sizes定义。
参数:
sizes (int...) - 整数序列,定义了输出张量的形状
out (Tensor, optinal) - 结果张量
torch.randn(*sizes, out=None) → Tensor 标准正态分布
返回一个张量,包含了从标准正态分布(均值为0,方差为1,即高斯白噪声)中抽取的一组随机数。张量的形状由参数sizes定义。
参数:
sizes (int...) - 整数序列,定义了输出张量的形状
out (Tensor, optinal) - 结果张量
torch.matmal(mat1, mat2)对矩阵mat1和mat2进行相乘。 如果mat1 是一个n×m张量,mat2 是一个 m×p 张量,将会输出一个 n×p 张量out。
torch.range(start=1, end=6) 的结果是会包含end的,
torch.arange(start=1, end=6)的结果并不包含end。
1.2 torch.matmul、mm和bmm的区别
-
mm只能进行矩阵乘法,也就是输入的两个tensor维度只能是mat1是(n * m),mat2是(m * p),得到的是(n * p)
-
matmul可以进行张量乘法, 输入可以是高维
-
bmm是两个batch之间的相乘
mat1是(batch * n * m),mat2是(batch * m * p),得到的是(batch * n * p)
1.3 nn.init 中实现参数的初始化函数
torch.nn.init.uniform_(tensor, a=0, b=1)均匀分布torch.nn.init.normal_(tensor, mean=0, std=1)正态分布torch.nn.init.constant_(tensor, val)初始化为常数val
1.4 为何要引入激活函数
- 不引入激活函数,全连接层就只对数据做仿射变换,多层仿射变换的叠加仍然是放射变换,解决方法是引入非线性变换,即激活函数
1.5 关于激活函数的选择
-
ReLu函数是一个通用的激活函数,目前在大多数情况下使用。但是,ReLU函数只能在隐藏层中使用。
-
用于分类器时,sigmoid函数及其组合通常效果更好。由于梯度消失问题,有时要避免使用sigmoid和tanh函数。
-
在神经网络层数较多的时候,最好使用ReLu函数,ReLu函数比较简单计算量少,而sigmoid和tanh函数计算量大很多。
-
在选择激活函数的时候可以先选用ReLu函数如果效果不理想可以尝试其他激活函数。
-
sigmoid的梯度消失是指输入值特别大或者特别小的时候求出来的梯度特别小,当网络较深,反向传播时梯度一乘就没有了,这是sigmoid函数的饱和特性导致的。ReLU在一定程度上优化了这个问题是因为用了max函数,对大于0的输入直接给1的梯度,对小于0的输入则不管。
但是ReLU存在将神经元杀死的可能性,这和他输入小于0那部分梯度为0有关,当学习率特别大,对于有的输入在参数更新时可能会让某些神经元直接失活,以后遇到什么样的输入输出都是0,Leaky ReLU输入小于0的部分用很小的斜率,有助于缓解这个问题。
为什么选择的激活函数普遍具有梯度消失的特点?
开始的时候我一直好奇为什么选择的激活函数普遍具有梯度消失的特点,这样不就让部分神经元失活使最后结果出问题吗?后来看到一篇文章的描述才发现,正是因为模拟人脑的生物神经网络的方法。在2001年有研究表明生物脑的神经元工作具有稀疏性,这样可以节约尽可能多的能量,据研究,只有大约1%-4%的神经元被激活参与,绝大多数情况下,神经元是处于抑制状态的,因此ReLu函数反而是更加优秀的近似生物激活函数。
所以第一个问题,抑制现象是必须发生的,这样能更好的拟合特征。
那么自然也引申出了第二个问题,为什么sigmoid函数这类函数不行?
1.中间部分梯度值过小(最大只有0.25)因此即使在中间部分也没有办法明显的激活,反而会在多层中失活,表现非常不好。
2.指数运算在计算中过于复杂,不利于运算,反而ReLu函数用最简单的梯度
在第二条解决之后,我们来看看ReLu函数所遇到的问题,
1.在负向部分完全失活,如果选择的超参数不好等情况,可能会出现过多神经元失活,从而整个网络死亡。
2.ReLu函数不是zero-centered,即激活函数输出的总是非负值,而gradient也是非负值,在back propagate情况下总会得到与输入x相同的结果,同正或者同负,因此收敛会显著受到影响,一些要减小的参数和要增加的参数会受到捆绑限制。
这两个问题的解决方法分别是
1.如果出现神经元失活的情况,可以选择调整超参数或者换成Leaky ReLu 但是,没有证据证明任何情况下都是Leaky-ReLu好
2.针对非zero-centered情况,可以选择用minibatch gradient decent 通过batch里面的正负调整,或者使用ELU(Exponential Linear Units)但是同样具有计算量过大的情况,同样没有证据ELU总是优于ReLU。
所以绝大多数情况下建议使用ReLu。
2 softmax回归
2.1 损失函数
-
平方损失函数
∥ y ^ ( i ) − y ( i ) ∥ 2 / 2 \|\boldsymbol{\hat y}^{(i)}-\boldsymbol{y}^{(i)}\|^2/2 ∥y^(i)−y(i)∥2/2
然而,想要预测分类结果正确,我们其实并不需要预测概率完全等于标签概率。例如,在图像分类的例子里,如果 y ( i ) = 3 y^{(i)}=3 y(i)=3,那么我们只需要 y ^ 3 ( i ) \hat{y}^{(i)}_3 y^3(i)比其他两个预测值 y ^ 1 ( i ) \hat{y}^{(i)}_1 y^1(i)和 y ^ 2 ( i ) \hat{y}^{(i)}_2 y^2(i)大就行了。即使 y ^ 3 ( i ) \hat{y}^{(i)}_3 y^3(i)值为0.6,不管其他两个预测值为多少,类别预测均正确。而平方损失则过于严格,例如 y ^ 1 ( i ) = y ^ 2 ( i ) = 0.2 \hat y^{(i)}_1=\hat y^{(i)}_2=0.2 y^1(i)=y^2(i)=0.2比 y ^ 1 ( i ) = 0 , y ^ 2 ( i ) = 0.4 \hat y^{(i)}_1=0, \hat y^{(i)}_2=0.4 y^1(i)=0,y^2(i)=0.4的损失要小很多,虽然两者都有同样正确的分类预测结果
-
交叉熵损失函数
交叉熵(cross entropy)是一个常用的衡量方法:
H ( y ( i ) , y ^ ( i ) ) = − ∑ j = 1 q y j ( i ) log y ^ j ( i ) , H\left(\boldsymbol y^{(i)}, \boldsymbol {\hat y}^{(i)}\right ) = -\sum_{j=1}^q y_j^{(i)} \log \hat y_j^{(i)}, H(y(i),y^(i))=−j=1∑qyj(i)logy^j(i),
交叉熵损失函数定义为
ℓ ( Θ ) = 1 n ∑ i = 1 n H ( y ( i ) , y ^ ( i ) ) , \ell(\boldsymbol{\Theta}) = \frac{1}{n} \sum_{i=1}^n H\left(\boldsymbol y^{(i)}, \boldsymbol {\hat y}^{(i)}\right ), ℓ(Θ)=n1i=1∑nH(y(i),y^(i)),最小化 ℓ ( Θ ) \ell(\boldsymbol{\Theta}) ℓ(Θ)等价于最大化 exp ( − n ℓ ( Θ ) ) = ∏ i = 1 n y ^ y ( i ) ( i ) \exp(-n\ell(\boldsymbol{\Theta}))=\prod_{i=1}^n \hat y_{y^{(i)}}^{(i)} exp(−nℓ(Θ))=∏i=1ny^y(i)(i),即最小化交叉熵损失函数等价于最大化训练数据集所有标签类别的联合预测概率。
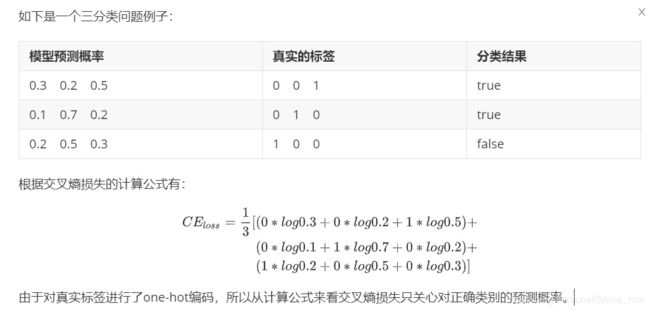
2.2 交叉熵损失函数
交叉熵的简单理解:
2.3 定义损失函数:
y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
y = torch.LongTensor([0, 2])
y_hat.gather(1, y.view(-1, 1))
对torch.gather()的理解:
torch.gather(input, dim, index, out=None) → Tensor
官方给出的解释是这样的:
沿给定轴dim,将输入索引张量index指定位置的值进行聚合。
对一个3维张量,输出可以定义为:
out[i][j][k] = tensor[index[i][j][k]][j][k] # dim=0
out[i][j][k] = tensor[i][index[i][j][k]][k] # dim=1
out[i][j][k] = tensor[i][j][index[i][j][k]] # dim=2
详细解释参考链接https://blog.csdn.net/Apikaqiu/article/details/104253080
2.4 画图
fig, ax = plt.subplots(1,3),其中参数1和3分别代表子图的行数和列数,一共有 1x3 个子图像。函数返回一个figure图像和子图ax的array列表。
fig, ax = plt.subplots(1,3,1),最后一个参数1代表第一个子图。
如果想要设置子图的宽度和高度可以在函数内加入figsize值
fig, ax = plt.subplots(1,3,figsize=(15,7)),这样就会有1行3个15x7大小的子图。
3 Pytorch定义模型
有两种方式:
-
继承
nn.Module,撰写自己的网络层一个
nn.Module实例应该包含一些层以及返回输出的前向传播(forward)方法以Pytorch定义softmax回归为例:
这里前面我们数据返回的每个batch样本
x的形状为(batch_size, 1, 28, 28),所以我们要先用view()将x的形状转换成(batch_size, 784)才送入全连接层。class LinearNet(nn.Module): def __init__(self, num_inputs, num_outputs): super(LinearNet, self).__init__() self.linear = nn.Linear(num_inputs, num_outputs) # forward 定义前向传播 def forward(self, x): # x shape: (batch, 1, 28, 28) y = self.linear(x.view(x.shape[0], -1)) return y net = LinearNet(num_inputs) print(net) # 使用print可以打印出网络的结构一般来说,需要修改的是:nn.Linear(num_inputs, num_outputs)中(num_inputs, num_outputs)按实际情况修改为实际的输入特征和输出,和self.linear()中x的形状是否需要转换
-
nn.SequentialSequential是一个有序的容器,网络层将按照在传入Sequential的顺序依次被添加到计算图中。以线性回归为例:
# 写法一 net = nn.Sequential( nn.Linear(num_inputs, num_outputs) # 此处还可以传入其他层 ) # 写法二 net = nn.Sequential() net.add_module('linear', nn.Linear(num_inputs, num_outputs)) # net.add_module ...... # 写法三 from collections import OrderedDict net = nn.Sequential(OrderedDict([ ('linear', nn.Linear(num_inputs, num_outputs)) # ...... ]))