TCN论文及代码解读总结

前言：传统的时序处理，普遍采用RNN做为基础网络模型，如其变体LSTM、GRU、BPTT等。但是在处理使用LSTM时时序的卷积神经网络

---

---

论文及代码链接

Paper:An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling
Code:Github:https://github.com/LOCUSLAB/tcn

---

一、论文解读

1、 摘要

   对于大多数deeplearning工作者，序列模型与RNN几乎是密不可分(这是因为RNN天生的循环自回归的结构是对时间序列的很好的表示)。然而，最新的一项研究表明，卷积结构在音频合成和机器翻译等tasks上效果可以优于递归神经网络。给定一个新的序列建模tasks或者是数据集，使用什么样的架构呢？论文对序列建模的通用卷积和递归结构进行了系统的评估。通过大量全面的标准tasks，对模型中进行评估，其中这些tasks通常用于递归网络的基准测试。论文研究表明，一个简单的卷积结构在不同的tasks和数据集上优于典型的递归神经网络，如LSTMs，同时卷积表现出更长的有效memory。论文的结论是序列建模和递归网络之间的共同联系应该重新考虑，卷积网络应该被认为是序列建模tasks的新的，自然的网路结构(natural starting point) 。

2、引言(摘)

  为了表示卷积网络，论文描述了一个通用的时间卷积网络（TCN）体系结构，它应用于所有的tasks。这种架构是由最近的研究进行了改进，特意保留了结构的简单性，结合了现代卷积架构的一些最佳实践经验。并与典型的递归体系结构（如LSTMs和GRUs）进行了比较。
  结果表明，TCNs在大量的序列建模任务中明显优于基线递归架构。这一点尤其值得注意，因为这些任务包括各种各样的基准，这些基准通常用于评估网络设计。这表明卷积结构最新在音频处理等应用中取得了成功，但并不局限于这些领域。
  为了进一步了解这些结论，作者深入分析了递归网络的记忆(memory)保持特性。结果表明，尽管递归结构理论上具有捕捉无限长时间的能力，但总的来说TCNs仍然表现出更长的记忆能力，TCNs更适用于长时间记忆的领域。
  总结：论文的研究是关于序列建模任务的卷积和递归结构的系统比较。结果表明，序列建模和递归网络之间的共同联系应该重新考虑。TCN体系结构不仅比LSTMs和GRUs等典型的递归网络更加精确，而且更加简单明了。因此，它可能是将深度网络应用于序列的更佳方法的起点(starting point)。

3、时序卷积神经网络(Temporal Convolutional Networks)

3.1 因果卷积(Causal Convolution)

  图片是是参考waveNet,可以用上图直观表示。 即对于上一层t时刻的值，只依赖于下一层t时刻及其之前的值。和传统的卷积神经网络的不同之处在于，因果卷积不能看到未来的数据，它是单向的结构，不是双向的。也就是说只有有了前面的因才有后面的果，是一种严格的时间约束模型，因此被成为因果卷积。但是问题就来，如果我要考虑很久之前的变量x，那么卷积层数就必须增加。卷积层数的增加就带来：梯度消失，训练复杂，拟合效果不好的问题，为了决绝这个问题，出现了扩展卷积（dilated）。

3.2 膨胀卷积(Dilated Convolution)

  对于因果卷积，存在的一个问题是需要很多层或者很大的filter来增加卷积的感受野。本文中，作者通过大小排列来的扩大卷积来增加感受野。扩大卷积（dilated convolution）是通过跳过部分输入来使filter可以应用于大于filter本身长度的区域。等同于通过增加零来从原始filter中生成更大的filter。d=1,2,4,8,16,…,膨胀系数为2的阶乘，膨胀卷积如上图所示。公式表达如下：$$F(s)=(x{\ast }_{d}f)(s)=\sum _{i=0}^{k-1}f(i)\cdot x_{s-d\cdot i}$$

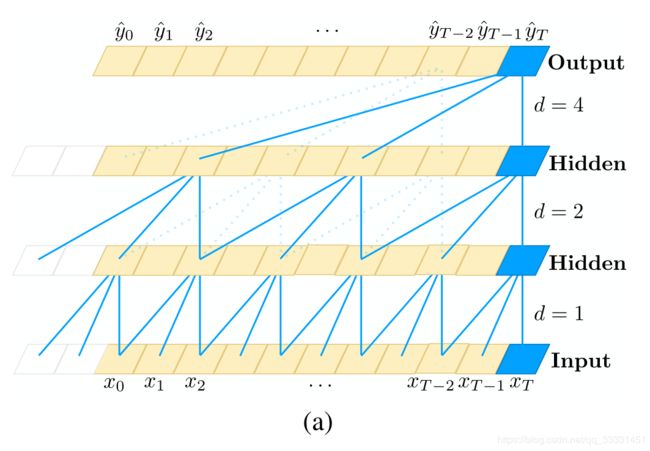
  论文采用的膨胀卷积为有"交叉"的一维卷积，膨胀系数d为1，2，4。

3.3 残差连接(Residual Connections)

我初次接触残差连接，是阅读何凯明大神的ResNet论文接触的，论文通过简单的残差连接，一定程度上消除了深度网络部分梯度消失和爆炸的影响。并且残差连接被证明是训练深层网络的有效方法，它使得网络可以以跨层的方式传递信息。论文构建了一个残差块，由于防止出现输入处理过程中出现维度变化，或者是为原始数据增加权重，增加训练参数。很多论文中都用到，例如CVPR2019的2s-GCN。如上图所示，一个残差块包含两层的卷积和非线性映射，在每层中还加入了WeightNorm和Dropout来正则化网络。

  总体来讲，TCN模型比较简，论文主要是将TCN的结构梳理了一下，感觉和wavenet很像，作者也说了参考了waveNet，加入了残差结构，并在很多的序列问题上进行了实验。实验效果如下：

二、源码解读

  论文给出了源代码，采用pytorch架构。由于是对TCN进行分析和总结，所以在不同的序列数据集上进行训练，证明了TCN结构的泛化能力。本小白将代码的主要结构简单的讲解，如有理解错误，希望大佬指正，不胜感激。
  以Mnist数据集为例mnist_pixel。作者将手写数字矩阵28x28矩阵，扩展成一维Sequence:1x784。batch_size=64,所以最后的序列结构为64x1x784。一张图片为1x784的序列矩阵，每一批次64张。论文代码简洁，清晰，有利于对TCN的深入了解。
TCN模型
剪枝,一维卷积后会出现多余的padding。

class Chomp1d(nn.Module):
    def __init__(self, chomp_size):
        super(Chomp1d, self).__init__()
        # 表示对继承自父类属性进行初始化
        self.chomp_size = chomp_size

    def forward(self, x):
        """
        其实这就是一个裁剪的模块，裁剪多出来的padding
        tensor.contiguous()会返回有连续内存的相同张量
        有些tensor并不是占用一整块内存，而是由不同的数据块组成
        tensor的view()操作依赖于内存是整块的，这时只需要执行
        contiguous()函数，就是把tensor变成在内存中连续分布的形式
        本函数主要是增加padding方式对卷积后的张量做切边而实现因果卷积
        """
        return x[:, :, :-self.chomp_size].contiguous()

时序模块,两层一维卷积，两层Weight_Norm,两层Chomd1d，非线性激活函数为Relu,dropout为0.2。

class TemporalBlock(nn.Module):
    def __init__(self, n_inputs, n_outputs, kernel_size, stride, dilation, padding, dropout=0.2):
        """
        相当于一个Residual block

        :param n_inputs: int, 输入通道数
        :param n_outputs: int, 输出通道数
        :param kernel_size: int, 卷积核尺寸
        :param stride: int, 步长，一般为1
        :param dilation: int, 膨胀系数
        :param padding: int, 填充系数
        :param dropout: float, dropout比率
        """
        super(TemporalBlock, self).__init__()
        self.conv1 = weight_norm(nn.Conv1d(n_inputs, n_outputs, kernel_size,
                                           stride=stride, padding=padding, dilation=dilation))
        # 经过conv1，输出的size其实是(Batch, input_channel, seq_len + padding)
        self.chomp1 = Chomp1d(padding)  # 裁剪掉多出来的padding部分，维持输出时间步为seq_len
        self.relu1 = nn.ReLU()
        self.dropout1 = nn.Dropout(dropout)

        self.conv2 = weight_norm(nn.Conv1d(n_outputs, n_outputs, kernel_size,
                                           stride=stride, padding=padding, dilation=dilation))
        self.chomp2 = Chomp1d(padding)  # 裁剪掉多出来的padding部分，维持输出时间步为seq_len
        self.relu2 = nn.ReLU()
        self.dropout2 = nn.Dropout(dropout)

        self.net = nn.Sequential(self.conv1, self.chomp1, self.relu1, self.dropout1,
                                 self.conv2, self.chomp2, self.relu2, self.dropout2)
        self.downsample = nn.Conv1d(n_inputs, n_outputs, 1) if n_inputs != n_outputs else None
        self.relu = nn.ReLU()
        self.init_weights()

    def init_weights(self):
        """
        参数初始化

        :return:
        """
        self.conv1.weight.data.normal_(0, 0.01)
        self.conv2.weight.data.normal_(0, 0.01)
        if self.downsample is not None:
            self.downsample.weight.data.normal_(0, 0.01)

    def forward(self, x):
        """
        :param x: size of (Batch, input_channel, seq_len)
        :return:
        """
        out = self.net(x)
        res = x if self.downsample is None else self.downsample(x)
        return self.relu(out + res)

时序卷积模块,使用for循环对8层隐含层，每层25个节点进行构建。模型如下。其中*layer不是c中的指针，困惑了笔者一段时间，之后查看资料知道 * 表示迭代器拆分layers为一层层网络。

class TemporalConvNet(nn.Module):
    def __init__(self, num_inputs, num_channels, kernel_size=2, dropout=0.2):
        """
        TCN，目前paper给出的TCN结构很好的支持每个时刻为一个数的情况，即sequence结构，
        对于每个时刻为一个向量这种一维结构，勉强可以把向量拆成若干该时刻的输入通道，
        对于每个时刻为一个矩阵或更高维图像的情况，就不太好办。

        :param num_inputs: int， 输入通道数
        :param num_channels: list，每层的hidden_channel数，例如[25,25,25,25]表示有4个隐层，每层hidden_channel数为25
        :param kernel_size: int, 卷积核尺寸
        :param dropout: float, drop_out比率
        """
        super(TemporalConvNet, self).__init__()
        layers = []
        num_levels = len(num_channels)
        for i in range(num_levels):
            dilation_size = 2 ** i  # 膨胀系数：1，2，4，8……
            in_channels = num_inputs if i == 0 else num_channels[i - 1]  # 确定每一层的输入通道数,输入层通道为1，隐含层是25。
            out_channels = num_channels[i]  # 确定每一层的输出通道数
            layers += [TemporalBlock(in_channels, out_channels, kernel_size, stride=1, dilation=dilation_size,
                                     padding=(kernel_size - 1) * dilation_size, dropout=dropout)]

        self.network = nn.Sequential(*layers)   # *作用是将输入迭代器拆成一个个元素

    def forward(self, x):
        """
        输入x的结构不同于RNN，一般RNN的size为(Batch, seq_len, channels)或者(seq_len, Batch, channels)，
        这里把seq_len放在channels后面，把所有时间步的数据拼起来，当做Conv1d的输入尺寸，实现卷积跨时间步的操作，
        很巧妙的设计。

        :param x: size of (Batch, input_channel, seq_len)
        :return: size of (Batch, output_channel, seq_len)
        """
        return self.network(x)

TCN模块,创新点1D·FCN，最后采用softmax进行分类。

class TCN(nn.Module):
    def __init__(self, input_size, output_size, num_channels, kernel_size, dropout):
        super(TCN, self).__init__()
        self.tcn = TemporalConvNet(input_size, num_channels, kernel_size=kernel_size, dropout=dropout)
        self.linear = nn.Linear(num_channels[-1], output_size)

    def forward(self, inputs):
        """Inputs have to have dimension (N, C_in, L_in)"""
        y1 = self.tcn(inputs)  # input should have dimension (N, C, L)
        o = self.linear(y1[:, :, -1])# 增加一个维度,1D·FCN
        return F.log_softmax(o, dim=1)

三、总结分析

通过网络图可知，TCN感受野可控，并且结构简单，速度更快。优缺点总结如下，感谢作者满腹的小不甘。

1、优点

（1）并行性。当给定一个句子时，TCN可以将句子并行的处理，而不需要像RNN那样顺序的处理。
（2）灵活的感受野。TCN的感受野的大小受层数、卷积核大小、扩张系数等决定。可以根据不同的任务不同的特性灵活定制。
（3）稳定的梯度。RNN经常存在梯度消失和梯度爆炸的问题，这主要是由不同时间段上共用参数导致的，和传统卷积神经网络一样，TCN不太存在梯度消失和爆炸问题。
（4）内存更低。RNN在使用时需要将每步的信息都保存下来，这会占据大量的内存，TCN在一层里面卷积核是共享的，内存使用更低。

2、缺点

（1）TCN 在迁移学习方面可能没有那么强的适应能力。这是因为在不同的领域，模型预测所需要的历史信息量可能是不同的。因此，在将一个模型从一个对记忆信息需求量少的问题迁移到一个需要更长记忆的问题上时，TCN 可能会表现得很差，因为其感受野不够大。
（2）论文中描述的TCN还是一种单向的结构，在语音识别和语音合成等任务上，纯单向的结构还是相当有用的。但是在文本中大多使用双向的结构，当然将TCN也很容易扩展成双向的结构，不使用因果卷积，使用传统的卷积结构即可。
（3）TCN毕竟是卷积神经网络的变种，虽然使用扩展卷积可以扩大感受野，但是仍然受到限制，相比于Transformer那种可以任意长度的相关信息都可以抓取到的特性还是差了点。TCN在文本中的应用还有待检验。

参考致谢

cv小白，学习借鉴，如有侵权，通知即删。如有出错，希望指正，不胜感激。
TCN时间卷积网络 - 剪水作花飞的文章 - 知乎
TCN-时间卷积网络-满腹的小不甘-CSDN
【NLP】因果卷积（causal）与扩展卷积（dilated）-阿木鸣
[1]:Bai S , Kolter J Z , Koltun V . An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling[J]. 2018.