深度学习PyTorch版学习笔记与心得（二）

多层感知机

    1.多层感知机的基本知识

      多层感知机（MLP）是研究神经网络的一个非常重要的多层模型。

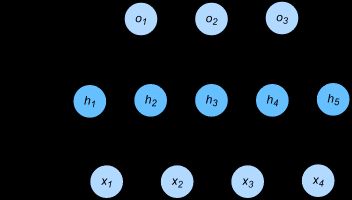
      下图展示了一个多层感知机的神经网络图，它含有一个隐藏层，该层中有5个隐藏单元。

 

表达公式：

      具体来说，给定一个小批量样本X∈Rn×dX∈Rn×d，其批量大小为nn，输入个数为dd。假设多层感知机只有一个隐藏层，其中隐藏单元个数为hh。记隐藏层的输出（也称为隐藏层变量或隐藏变量）为HH，有H∈Rn×hH∈Rn×h。因为隐藏层和输出层均是全连接层，可以设隐藏层的权重参数和偏差参数分别为Wh∈Rd×hWh∈Rd×h和 bh∈R1×hbh∈R1×h，输出层的权重和偏差参数分别为Wo∈Rh×qWo∈Rh×q和bo∈R1×qbo∈R1×q。

激活函数：

      上述问题的根源在于全连接层只是对数据做仿射变换（affine transformation），而多个仿射变换的叠加仍然是一个仿射变换。解决问题的一个方法是引入非线性变换，例如对隐藏变量使用按元素运算的非线性函数进行变换，然后再作为下一个全连接层的输入。这个非线性函数被称为激活函数。

    2.使用多层感知机图像分类的从零开始的实现

代码如下：

import torch
import numpy as np
import sys
sys.path.append("/home/kesci/input")
import d2lzh1981 as d2l
print(torch.__version__)
# 获取训练集
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size,root='/home/kesci/input/FashionMNIST2065')
#定义激活函数
def relu(X):
    return torch.max(input=X, other=torch.tensor(0.0))
#定义网络
def net(X):
    X = X.view((-1, num_inputs))
    H = relu(torch.matmul(X, W1) + b1)
    return torch.matmul(H, W2) + b2
#定义损失函数
loss = torch.nn.CrossEntropyLoss()

    3.使用pytorch的简洁实现

num_inputs, num_outputs, num_hiddens = 784, 10, 256
    
net = nn.Sequential(
        d2l.FlattenLayer(),
        nn.Linear(num_inputs, num_hiddens),
        nn.ReLU(),
        nn.Linear(num_hiddens, num_outputs), 
        )
    
for params in net.parameters():
    init.normal_(params, mean=0, std=0.01)

过拟合、欠拟合及其解决方案

      在解释上述现象之前，我们需要区分训练误差（training error）和泛化误差（generalization error）。通俗来讲，前者指模型在训练数据集上表现出的误差，后者指模型在任意一个测试数据样本上表现出的误差的期望，并常常通过测试数据集上的误差来近似。计算训练误差和泛化误差可以使用之前介绍过的损失函数，例如线性回归用到的平方损失函数和softmax回归用到的交叉熵损失函数。

      机器学习模型应关注降低泛化误差。

      模型训练中经常出现的两类典型问题：

• 一类是模型无法得到较低的训练误差，我们将这一现象称作欠拟合（underfitting）；
• 另一类是模型的训练误差远小于它在测试数据集上的误差，我们称该现象为过拟合（overfitting）。 在实践中，我们要尽可能同时应对欠拟合和过拟合。虽然有很多因素可能导致这两种拟合问题，在这里我们重点讨论两个因素：模型复杂度和训练数据集大小。

      权重衰减：

      权重衰减等价于 L2L2 范数正则化（regularization）。正则化通过为模型损失函数添加惩罚项使学出的模型参数值较小，是应对过拟合的常用手段。

      丢弃法：

      多层感知机中神经网络图描述了一个单隐藏层的多层感知机。其中输入个数为4，隐藏单元个数为5，且隐藏单元hihi（i=1,…,5i=1,…,5）的计算表达式为       hi=ϕ(x1w1i+x2w2i+x3w3i+x4w4i+bi)

梯度消失、梯度爆炸

      深度模型有关数值稳定性的典型问题是消失（vanishing）和爆炸（explosion）。在神经网络中，通常需要随机初始化模型参数。在Pytorch中有默认随机初始化，使用torch.nn.init.normal_()使模型net的权重参数采用正态分布的随机初始化方式。

      考虑到环境因素：

1. 协变量偏移
2. 标签偏移
3. 概念偏移