膜拜(离散化差分模板题)

题目描述
小鱼有 n 名优秀的粉丝。

粉丝们得知小鱼将会在一条直线上出现，打算去膜他。为了方便，粉丝们在这条直线上建立数轴。

第 i 名粉丝有一个侦查区间[li,ri] 。如果小鱼在 j(li≤j≤ri) 处出现，这名粉丝将立刻发现并膜他。

小鱼希望膜他的人越多越好，但是他不能分身，因此只能选择一个位置出现。

小鱼想知道自己最多能被多少个人膜。
输入
第一行一个整数n —— 粉丝的个数。

接下来 n 行，每行两个整数 li,ri ，分别表示第 i 名粉丝的侦查区间的两个端点。两个数之间用空格隔开。
输出
共一行，一个整数，表示小鱼最多能被多少人膜。
样例输入

4
3 5
4 8
1 2
5 10

样例输出
3
提示
样例解释：

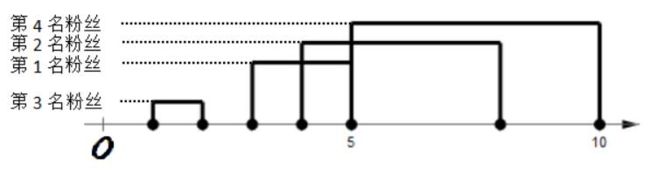
如图所示，小鱼可出现在5处，此时第1,2,4号粉丝可以膜他。小鱼最多只能被3个粉丝膜。

对于20%的数据，n≤2
对于60%的数据，n≤2000
对于100%的数据，1 ≤ n ≤ 5 × 10⁴,1 ≤ li ≤ ri <2³⁰

这个题很容易就可以想起来差分数组，但是以看数据范围，有点感人，因此需要进行离散化
模板题没什么好说的

#include 
using namespace std;
#define wuyt main
typedef long long ll;
template<class T> inline T min(T &x,const T &y){return x>y?y:x;}
template<class T> inline T max(T &x,const T &y){return x<y?y:x;}
ll read(){ll c = getchar(),Nig = 1,x = 0;while(!isdigit(c) && c!='-')c = getchar();
    if(c == '-')Nig = -1,c = getchar();
    while(isdigit(c))x = ((x<<1) + (x<<3)) + (c^'0'),c = getchar();
    return Nig*x;}
#define read read()
ll maxx=-1,minn=inf;
ll num[maxn],a[maxn],num2[maxn];
ll res,ans;
int n;
ll cnt[maxn];
pair<ll,ll> together[maxn];
vector <ll> vet;
int main()
{
    n=read;
    for(int i=1;i<=n;i++){
        ll left=read,right=read;
        vet.push_back(left);
        vet.push_back(right);
        together[i]={left,right};
    }
    sort(vet.begin(),vet.end());
    vet.erase(unique(vet.begin(),vet.end()),vet.end());

    for(int i=1;i<=n;i++){
        ll left=together[i].first;
        ll right=together[i].second;
        ll templeft=lower_bound(vet.begin(),vet.end(),left)-vet.begin();
        ll tempright=lower_bound(vet.begin(),vet.end(),right)-vet.begin();
        num[templeft]+=1;
        num[tempright+1]-=1;
    }
    int len=vet.size();
    for(int i=1;i<len;i++) num[i]+=num[i-1];
    ans=num[0];
    for(int i=1;i<len;i++)
        if(num[i]>=ans)
            ans=num[i];
    cout<<ans<<endl;
    return 0;
}