最全莫烦pytorch学习笔记基础部分
一、作者简介
作者:周沫凡 Mofan Zhou , 所以 “莫烦” 这个名字也是取了个谐音而已. 他就用名字鼓励大家. 即使遇到再多再大的困难, 我们还是要抱着一种 莫烦 的态度, 努力到底.
原本, 他只是一名普普通通的 PhD 学生, 因为专业不对口, 之前学的东西在 PhD 的时候统统用不上, 然后我就开始了我漫长的自学道路. 你在这个网页看到的所有内容, 都是我在网上探索, 自学而来的. 所以说, 真正的大学, 其实就是锻炼你自学能力的地方. 我很欣赏网上那些默默奉献的人们, 分享自己所学的东西给了我. 所以这就是我创建 优酷 和 Youtube 个人频道的萌芽. 我也要回报那些奉献的人们, 将我的所学奉献给大家~
详情可以看此网站:https://morvanzhou.github.io/about/
二、pytorch课程简介
PyTorch 是 PyTorch 在 Python 上的衍生. 因为 PyTorch 是一个使用 PyTorch 语言的神经网络库, Torch 很好用, 但是 Lua 又不是特别流行, 所有开发团队将 Lua 的 Torch 移植到了更流行的语言 Python 上. 是的 PyTorch 一出生就引来了剧烈的反响。莫烦老师教课生动有趣,通俗易懂,比较适合初学者。而且都是免费的。
课程网址;https://morvanzhou.github.io/tutorials/machine-learning/torch/1-1-A-ANN-and-NN/
三、Pytorch 教程
3.1 Pytorch and Numpy
3.1.1 用Torch or Numpy
Pytorch发布已经有一段时间了,我们在使用中也发现了其独特的动态图设计,让我们可以高效地进行神经网络的构造、实现我们的想法。那么Pytorch是怎么来的,追根溯源,pytorch可以说是torch的python版,然后增加了很多新的特性(pytorch与torch的区别可以看:https://cloud.tencent.com/developer/article/1142510)。
Torch 自称为神经网络界的 Numpy, 因为他能将 torch 产生的 tensor 放在 GPU 中加速运算 (前提是你有合适的 GPU), 就像 Numpy 会把 array 放在 CPU 中加速运算. 所以神经网络的话, 当然是用 Torch 的 tensor 形式数据最好咯. 就像 Tensorflow 当中的 tensor 一样.
numpy在科学计算运用还是很广泛的,我们比较喜欢numpy是因为我们较为早的接触到numpy,熟悉了它的形式。而torch为了是使用者运用类比的方式使用torch,他们把torch 做的和 numpy 能很好的兼容。即它们之间可以相互转换:
numpy array 转换成 torch tensor :torch.from_numpy(np_data)
torch tensor 转换成 numpy array:torch_data.numpy()
import torch
import numpy as np
from torch.autograd import Variable
#1.1 numpy and tensor
np_data = np.arange(6).reshape(2,3)
torch_data = torch.from_numpy(np_data)
tensor2array = torch_data.numpy()
print(
'\nnumpy array:', '\n' ,np_data,
'\ntorch tensor:','\n' , torch_data,
'\ntensor to array:','\n', tensor2array,
)
3.1.2 torch 中的数学运算
对于torch中的tensor和numpy array的运算类比一下,其实它们形式差不多的,如果了解 torch 中其它更多有用的运算符, 可以参考Pytorch中文手册.
1)abs绝对值计算
#1.2abs
data = [-1, -2, 1, 2]
tensor = torch.FloatTensor(data) # 转换成32位浮点 tensor
print(
'\nabs',
'\nnumpy: ', np.abs(data), # [1 2 1 2]
'\ntorch: ', torch.abs(tensor) # [1 2 1 2]
)
2)sin三角函数
print(
'\nsin',
'\nnumpy: ', np.sin(data), # [-0.84147098 -0.90929743 0.84147098 0.90929743]
'\ntorch: ', torch.sin(tensor) # [-0.8415 -0.9093 0.8415 0.9093]
)
3)mean均值
print(
'\nsin',
'\nnumpy: ', np.sin(data), # [-0.84147098 -0.90929743 0.84147098 0.90929743]
'\ntorch: ', torch.sin(tensor) # [-0.8415 -0.9093 0.8415 0.9093]
)
三次运算的结果:

除了简单的计算, 矩阵运算才是神经网络中最重要的部分. 所以我们展示下矩阵的乘法. 注意一下包含了一个 numpy 中可行, 但是 torch 中不可行的方式
4)matrix multiplication 矩阵点乘
#1.3 matrix multiplication 矩阵点乘
data = [[1,2], [3,4]]
tensor = torch.FloatTensor(data) # 转换成32位浮点 tensor
# correct method
print(
'\nmatrix multiplication (matmul)',
'\nnumpy: ','\n', np.matmul(data, data), # [[7, 10], [15, 22]]
'\ntorch: ', '\n',torch.mm(tensor, tensor) # [[7, 10], [15, 22]]
)
# !!!! 下面是错误的方法 !!!!
data = np.array(data)
print(
'\nmatrix multiplication (dot)',
'\nnumpy: ', data.dot(data), # [[7, 10], [15, 22]] 在numpy 中可行
'\ntorch: ',tensor.dot(tensor) # torch.dot只能处理一维数组
)
3.2 Varial 变量
3.2.1 什么是Varial
在 Torch 中的 Variable 就是一个存放会变化的值的地理位置. 里面的值会不停的变化。就像一个裝鸡蛋的篮子, 鸡蛋数会不停变动.。那谁是里面的鸡蛋呢, 自然就是 Torch 的 Tensor 咯. 如果用一个 Variable 进行计算, 那返回的也是一个同类型的 Variable。**(原教程这样说的,但是Facebook 推出了 PyTorch 0.4.0 版本,该版本有诸多更新和改变,比如支Windows,Variable 和 Tensor 合并等等,详细介绍请查看文章《Pytorch 重磅更新**》)
代码如下:
#1.4 variable
#首先创建鸡蛋
tensor1 = torch.FloatTensor([[1,2],[3,4]])
# 其次把鸡蛋放到篮子里, requires_grad是参不参与误差反向传播, 要不要计算梯度
variable = Variable(tensor1, requires_grad = True) #反向传播
print(tensor1)
print(variable)
3.2.2 Variable 计算 and grap
我们首先将tensor的计算与varianle计算对比一下,看看其中的区别:
#1.5 Variable calculation gradient
tensor1 = torch.FloatTensor([[1,2],[3,4]])
# 其次把鸡蛋放到篮子里, requires_grad是参不参与误差反向传播, 要不要计算梯度
variable = Variable(tensor1, requires_grad = True) #反向传播
t_out = torch.mean(tensor1*tensor1)
v_out = torch.mean(variable*variable)
print(t_out)
print(v_out)
执行结果:

到目前为止, 我们看不出什么不同, 但是时刻记住, Variable 计算时, 它在背景幕布后面一步步默默地搭建着一个庞大的系统, 叫做计算图(computational graph). 这个图是用来干嘛的? 原来是将所有的计算步骤 (节点) 都连接起来, 最后进行误差反向传递的时候, 一次性将所有 variable 里面的修改幅度 (梯度) 都计算出来, 而 tensor 就没有这个能力啦。
v_out = torch.mean(variable*variable) 就是在计算图中添加的一个计算步骤, 计算误差反向传递的时候有他一份功劳, 我们就来举个例子:
#1.6 variable
#首先创建鸡蛋
tensor1 = torch.FloatTensor([[1,2],[3,4]])
# 其次把鸡蛋放到篮子里, requires_grad是参不参与误差反向传播, 要不要计算梯度
variable = Variable(tensor1, requires_grad = True) #反向传播
t_out = torch.mean(tensor1*tensor1)
v_out = torch.mean(variable*variable)
v_out.backward() # 模拟 v_out 的误差反向传递
# 下面两步看不懂没关系, 只要知道 Variable 是计算图的一部分, 可以用来传递误差就好.
# v_out = 1/4 * sum(variable*variable) 这是计算图中的 v_out 计算步骤
# 针对于 v_out 的梯度就是, d(v_out)/d(variable) = 1/4*2*variable = variable/2
print(variable.grad) # 初始 Variable 的梯度
3.2.3 获取Variable里的数据
代码如下:
#1.7 to get variable data
#首先创建鸡蛋
tensor1 = torch.FloatTensor([[1,2],[3,4]])
# 其次把鸡蛋放到篮子里, requires_grad是参不参与误差反向传播, 要不要计算梯度
variable = Variable(tensor1, requires_grad = True) #反向传播
t_out = torch.mean(tensor1*tensor1)
v_out = torch.mean(variable*variable)
v_out.backward() # 模拟 v_out 的误差反向传递
# 下面两步看不懂没关系, 只要知道 Variable 是计算图的一部分, 可以用来传递误差就好.
# v_out = 1/4 * sum(variable*variable) 这是计算图中的 v_out 计算步骤
# 针对于 v_out 的梯度就是, d(v_out)/d(variable) = 1/4*2*variable = variable/2
print(variable.grad) # 初始 Variable 的梯度
print(variable) # Variable 形式
print(variable.data) # tensor 形式
print(variable.data.numpy()) # numpy 形式
3.3 Torch中的激励函数
Torch中的激励函数有很多,我们常用的有:relu,sigmoid,tanh,softplus。
代码如下:
#active function :relu sigmoid tanch softplus
import torch
from torch.autograd import Variable
import torch.nn.functional as F # active function
import matplotlib.pyplot as plt #显示库
#fake data
x = torch.linspace(-5,5,500) # x data (tensor),shape=(100,1)
x = Variable(x)
x_np = x.data.numpy() #换成numpy array数据,用于画图
#常见的激励函数
y_relu = torch.relu(x).data.numpy()
y_sigmoid = torch.sigmoid(x).data.numpy()
y_tanh = torch.tanh(x).data.numpy()
y_softplus = F.softplus(x).data.numpy()
#画图部分
plt.figure(1,figsize=(8,6))#画图的一个画布,figsize画布大小
plt.subplot(221)
plt.plot(x_np,y_relu,c='red',label='relu')
plt.ylim((-1,5)) #y轴的范围
plt.legend(loc='best') #展示每条线的标识
plt.subplot(222)
plt.plot(x_np,y_sigmoid,c='blu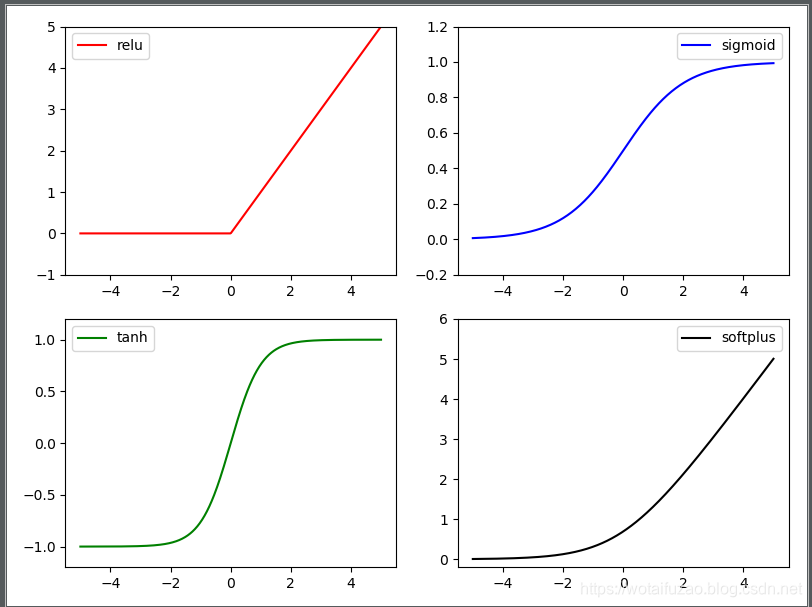,label='sigmoid')
plt.ylim((-0.2,1.2))
plt.legend(loc='best')
plt.subplot(223)
plt.plot(x_np,y_tanh,c='green',label='tanh')
plt.ylim((-1.2,1.2))
plt.legend(loc='best')
plt.subplot(224)
plt.plot(x_np,y_softplus,c='black',label='softplus')
plt.ylim((-0.2,6))
plt.legend(loc='best')
plt.show()
执行结果:

注意:
y_relu = torch.relu(x).data.numpy()
y_sigmoid = torch.sigmoid(x).data.numpy()
y_tanh = torch.tanh(x).data.numpy()
这是新版本的调用方式,老版本的是从torch.nn.functional 模块调用的,已经被摒弃了。
建造一个神经网络
3.4关系拟合
如何在数据当中找到他们的关系, 然后用神经网络模型来建立一个可以代表他们关系的线条。
3.4.1 建立数据集
我们创建一些假数据来模拟真实的情况. 比如一个一元二次函数: y = a * x^2 + b, 我们给 y 数据加上一点噪声来更加真实的展示它。
代码如下:
import torch
from torch.autograd import Variable
import matplotlib.pyplot as plt
x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1) # x data (tensor), shape=(100, 1)
y = x.pow(2) + 0.2*torch.rand(x.size()) # noisy y data (tensor), shape=(100, 1)
# 用 Variable 来修饰这些数据 tensor
x, y = torch.autograd.Variable(x), Variable(y)
# 画图
plt.scatter(x.data.numpy(), y.data.numpy(),c="green")
plt.show()
关于unsqueenze用法和理解可以参考,此blog
其执行结果:

3.4.2 建立神经网络
建立一个神经网络我们可以直接运用 torch 中的体系, 先定义所有的层属性(init()), 然后再一层层搭建(forward(x))层于层的关系链接。 建立关系的时候, 我们会用到激励函数。
代码如下:
import torch #导入torch
import torch.nn.functional as F # 激励函数
class Net(torch.nn.Module): # 继承 torch 的 Module
#此层只是初始化
def __init__(self, n_feature, n_hidden, n_output):
super(Net, self).__init__() # 继承 __init__ 功能
# 定义每层用什么样的形式
self.hidden = torch.nn.Linear(n_feature, n_hidden) # 隐藏层线性输出
self.predict = torch.nn.Linear(n_hidden, n_output) # 输出层线性输出
#此层搭建神经网络
def forward(self, x): # 这同时也是 Module 中的 forward 功能
# 正向传播输入值, 神经网络分析出输出值
x = F.relu(self.hidden(x)) # 激励函数(隐藏层的线性值)
x = self.predict(x) # 输出值
return x
net = Net(n_feature=1, n_hidden=10, n_output=1) #一个特征,10个隐藏层,一个输出
print(net) # net 的结构
3.4.3 训练网络
其训练步骤如下:在上面代码基础上加入下面代码
# optimizer 是训练的工具
optimizer = torch.optim.SGD(net.parameters(), lr=0.5) # 传入 net 的所有参数, 学习率
loss_func = torch.nn.MSELoss() # 预测值和真实值的误差计算公式 (均方差),多用于拟合
for t in range(100):
prediction = net(x) # 喂给 net 训练数据 x, 输出预测值
loss = loss_func(prediction, y) # 计算两者的误差,prediction要在前,真实值在后
optimizer.zero_grad() # 清空上一步的残余更新参数值
loss.backward() # 误差反向传播, 计算参数更新值
optimizer.step() # 将参数更新值施加到 net 的 parameters 上
3.4.4 可视化训练
为了形象的理解训练的结果,我们将将进行下面操作:
import matplotlib.pyplot as plt
plt.ion() # 画图
plt.show()
for t in range(100):
...
loss.backward()
optimizer.step()
# 接着上面来
if t % 5 == 0:
# plot and show learning process
plt.cla()
plt.scatter(x.data.numpy(), y.data.numpy())
plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)
plt.text(0.5, 0, 'Loss=%.4f' % loss.data[0], fontdict={'size': 20, 'color': 'red'})
plt.pause(0.1)
3.5 分类
这节主要讲一点用简单的神经网络进行分类。
3.5.1建立数据集
一开始,我们创建一些模拟数据,比如两个二项分布的数据。但是它们的均值是不一样的。
代码如下:
import torch
from torch.autograd import Variable
import matplotlib.pyplot as plt
# fake data
n_data = torch.ones(100, 2) # 数据的基本形态
x0 = torch.normal(2*n_data, 1) # 类型0 x data (tensor), shape=(100, 2)
y0 = torch.zeros(100) # 类型0 y data (tensor), shape=(100, 1)
x1 = torch.normal(-2*n_data, 1) # 类型1 x data (tensor), shape=(100, 2)
y1 = torch.ones(100) # 类型1 y data (tensor), shape=(100, 1)
# 注意 x, y 数据的数据形式是一定要像下面一样 (torch.cat 是在合并数据)
x = torch.cat((x0, x1), 0).type(torch.FloatTensor) # shape (200,2)FloatTensor = 32-bit floating
y = torch.cat((y0, y1), ).type(torch.LongTensor) # shape(200,)LongTensor = 64-bit integer(标签默认)
# torch 只能在 Variable 上训练, 所以把它们变成 Variable
x, y = Variable(x), Variable(y)
# show
plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=y.data.numpy(), s=100, lw=0, cmap='RdYlBu')
plt.show()
执行结果:
3.5.2 建立神网络
我们在建立神经网络时,可以直接运用torch中的体系。首先定义所有层属性(init()),然后再一层一层搭建(forward())层与层之间关系链路。这和我们再上节中的regression的神经网络差不多。
代码如下:
import torch
from torch.autograd import Variable
import matplotlib.pyplot as plt
import torch.nn.functional as F
# fake data
n_data = torch.ones(100, 2) # 数据的基本形态
x0 = torch.normal(2*n_data, 1) # 类型0 x data (tensor), shape=(100, 2)
y0 = torch.zeros(100) # 类型0 y data (tensor), shape=(100, 1)
x1 = torch.normal(-2*n_data, 1) # 类型1 x data (tensor), shape=(100, 2)
y1 = torch.ones(100) # 类型1 y data (tensor), shape=(100, 1)
# 注意 x, y 数据的数据形式是一定要像下面一样 (torch.cat 是在合并数据)
x = torch.cat((x0, x1), 0).type(torch.FloatTensor) # shape (200,2)FloatTensor = 32-bit floating
y = torch.cat((y0, y1), ).type(torch.LongTensor) # shape(200,)LongTensor = 64-bit integer
# torch 只能在 Variable 上训练, 所以把它们变成 Variable
x, y = Variable(x), Variable(y)
# show
# plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=y.data.numpy(), s=100, lw=0, cmap='RdYlGn')
# plt.show()
class Net(torch.nn.Module): # 继承 torch 的 Module
def __init__(self, n_feature, n_hidden, n_output):
super(Net, self).__init__() # 继承 __init__ 功能
self.hidden = torch.nn.Linear(n_feature, n_hidden) # 隐藏层线性输出
self.out = torch.nn.Linear(n_hidden, n_output) # 输出层线性输出
def forward(self, x):
# 正向传播输入值, 神经网络分析出输出值
x = F.relu(self.hidden(x)) # 激励函数(隐藏层的线性值)
x = self.out(x) # 输出值, 但是这个不是预测值, 预测值还需要再另外计算
return x
net = Net(n_feature=2, n_hidden=10, n_output=2) # 几个类别就几个 output
print(net) # net 的结构
3.5.3 训练网路
代码如下:
# optimizer 是优化工具
optimizer = torch.optim.SGD(net.parameters(), lr=0.02) # 传入 net 的所有参数, 学习率
# 算误差的时候, 注意真实值!不是! one-hot 形式的, 而是1D Tensor, (batch,)
# 但是预测值是2D tensor (batch, n_classes)
loss_func = torch.nn.CrossEntropyLoss() #此损失函数多用于分类
for t in range(100):
out = net(x) # 喂给 net 训练数据 x, 输出分析值。输出的是[-2.-0.12,20]再用F.softmax(out)转化概率
loss = loss_func(out, y) # 计算两者的误差
optimizer.zero_grad() # 清空上一步的残余更新参数值
loss.backward() # 误差反向传播, 计算参数更新值
optimizer.step() # 将参数更新值施加到 net 的 parameters 上
3.5.4 可视化训练过程
为了可视化,我们加入以下代码:
import matplotlib.pyplot as plt
plt.ion() # 画图
plt.show()
for t in range(100):
...
loss.backward()
optimizer.step()
# 接着上面来
if t % 2 == 0:
plt.cla()
# 过了一道 softmax 的激励函数后的最大概率才是预测值
prediction = torch.max(F.softmax(out, dim=1), 1)[1]
pred_y = prediction.data.numpy().squeeze()
target_y = y.data.numpy()
plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=pred_y, s=100, lw=0, cmap='RdYlGn')
accuracy = sum(pred_y == target_y)/200 # 预测中有多少和真实值一样
plt.text(1.5, -4, 'Accuracy=%.2f' % accuracy, fontdict={'size': 20, 'color': 'red'})
plt.pause(0.1)
plt.ioff() # 停止画图
plt.show()
3.6快速搭建法
本小节,运用Torch中提供的方法,来快速搭建神经网络,并怎么保存和加载参数。
3.6.1 快速搭建
我们可以先看看上节用的神经网络的步骤,用net1表示此搭建方法。
具体代码如下:
import torch
import torch.nn.functional as F
# 此代码将被快速搭建代替
class Net(torch.nn.Module):
def __init__(self, n_feature, n_hidden, n_output):
super(Net, self).__init__()
self.hidden = torch.nn.Linear(n_feature, n_hidden) # hidden layer
self.predict = torch.nn.Linear(n_hidden, n_output) # output layer
def forward(self, x):
x = F.relu(self.hidden(x)) # activation function for hidden layer
x = self.predict(x) # linear output
return x
net1 = Net(1, 10, 1)
# 快速搭建法
net2 = torch.nn.Sequential(
torch.nn.Linear(1, 10),
torch.nn.ReLU(),
torch.nn.Linear(10, 1)
)
#对比两个区别
print(net1) # net1 architecture
print(net2) # net2 architecture
执行结果如下:

从上面代码可以看出,原来代码是用了class继承了一个torch中的神经网络结构,然后对其修改。而快速搭建方法就用一句话概括了上面的所有的内容。即net2部分的代码。
对比一下执行的结果来看:
我们会发现 net2 多显示了一些内容, 这是为什么呢? 原来他把激励函数也一同纳入进去了, net1 中, 激励函数实际上是在 forward() 功能中才被调用的. 这也就说明了,比 net2, net1 的好处就是, 你可以根据你的个人需要更加个性化你自己的前向传播过程, 比如(RNN). 不过如果你不需要七七八八的过程, 相信 net2 这种形式更适合你。
3.6.2保存提取
1)保存
此次用快速搭建网络:
import torch
import matplotlib.pyplot as plt
# torch.manual_seed(1) # reproducible
# fake data数据生成
x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1) # x data (tensor), shape=(100, 1)
y = x.pow(2) + 0.2*torch.rand(x.size()) # noisy y data (tensor), shape=(100, 1)
def save():
# 建立网络
net1 = torch.nn.Sequential(
torch.nn.Linear(1, 10), #一个输入,10个隐藏层
torch.nn.ReLU(), #激活函数
torch.nn.Linear(10, 1) #一个输出
)
optimizer = torch.optim.SGD(net1.parameters(), lr=0.5) #选择的优化方法
loss_func = torch.nn.MSELoss() #选择的损失函数
#训练网络
for t in range(100):
prediction = net1(x) #对x进行预测
loss = loss_func(prediction, y) #计算损失值
optimizer.zero_grad() #清空上次迭代的梯度
loss.backward() #反向传播
optimizer.step() #更新梯度
我们有两种方式来保存数据:
torch.save(net1, 'net.pkl') # 保存整个网络
torch.save(net1.state_dict(), 'net_params.pkl') # 只保存网络中的参数 (速度快, 占内存少)
2)提取整个网络
代码如下:
def restore_net():
# restore entire net1 to net2
net2 = torch.load('net.pkl')
prediction = net2(x)
这种方式将会提取整个网络,网络很大时可能会就比较慢。
3)只提取网络参数
代码如下:
def restore_params():
# 新建 net3
net3 = torch.nn.Sequential(
torch.nn.Linear(1, 10),
torch.nn.ReLU(),
torch.nn.Linear(10, 1)
)
# 将保存的参数复制到 net3
net3.load_state_dict(torch.load('net_params.pkl'))
prediction = net3(x)
3.6.3 显示结果
调用上面的功能函数,再加上画图模块:
# 保存 net1 (1. 整个网络, 2. 只有参数)
save()
# 提取整个网络
restore_net()
# 提取网络参数, 复制到新网络
restore_params()
执行结果:

对比一下,三个网络没有区别。
本节总结:完整代码在此
3.7批量训练
Torch 中提供了一种帮你整理你的数据结构的好东西, 叫做 DataLoader, 我们能用它来包装自己的数据, 进行批训练。
3.7.1DataLoader
DataLoader 是 torch 给你用来包装你的数据的工具。你要讲自己的 (numpy array 或其他) 数据形式装换成 Tensor, 然后再放进这个包装器中. 使用 DataLoader 有什么好处呢? 就是他们帮你有效地迭代数据, 举例:
import torch
import torch.utils.data as Data
torch.manual_seed(1) # reproducible
BATCH_SIZE = 5 #批量训练数据个数
# BATCH_SIZE = 8
x = torch.linspace(1, 10, 10) # this is x data (torch tensor)
y = torch.linspace(10, 1, 10) # this is y data (torch tensor)
torch_dataset = Data.TensorDataset(x, y) #转换torch能识别的dataset
#把dataset放入DataLoader中
loader = Data.DataLoader(
dataset=torch_dataset, # torch TensorDataset format
batch_size=BATCH_SIZE, # mini batch size
shuffle=True, # random shuffle for training 要不要打乱数据
num_workers=2, # subprocesses for loading data 多线程读数据
)
#show
def show_batch():
for epoch in range(3): # train entire dataset 3 times
for step, (batch_x, batch_y) in enumerate(loader): # for each training step
# train your data...
print('Epoch: ', epoch, '| Step: ', step, '| batch x: ',
batch_x.numpy(), '| batch y: ', batch_y.numpy())
if __name__ == '__main__':
show_batch()
执行结果:

可以看出, 每步都导出了5个数据进行学习。每个 epoch 的导出数据都是先打乱了以后再导出。
真正方便的还不是这点,我们改变一下 BATCH_SIZE = 8, 这样我们就知道, step=0 会导出8个数据, 但是, step=1 时数据库中的数据不够 8个, 这时怎么办呢。执行结果:

这时, 在 step=1 就只给你返回这个 epoch 中剩下的数据就好了。
3.8 加速神经网络训练——优化器
加速你的神经网络训练过程包括以下几种模式:
- Stochastic Gradient Descent (SGD)
- Momentum
- AdaGrad
- RMSProp
- Adam
相关资料可以参考:此blog
3.8.1 伪数据
代码如下:
import torch
import matplotlib.pyplot as plt
# torch.manual_seed(1) # reproducible
LR = 0.01
BATCH_SIZE = 32
EPOCH = 12
# fake dataset
x = torch.unsqueeze(torch.linspace(-1, 1, 1000), dim=1)
y = x.pow(2) + 0.1*torch.normal(torch.zeros(*x.size()))
# plot dataset
plt.scatter(x.numpy(), y.numpy(),c="red")
plt.show()
3.8.2 创建各个优化器对应的Net
为了对比每一种优化器, 我们给他们各自创建一个神经网络, 但这个神经网络都来自同一个 Net 形式。
# 默认的 network 形式
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.hidden = torch.nn.Linear(1, 20) # hidden layer
self.predict = torch.nn.Linear(20, 1) # output layer
def forward(self, x):
x = F.relu(self.hidden(x)) # activation function for hidden layer
x = self.predict(x) # linear output
return x
# 为每个优化器创建一个 net
net_SGD = Net()
net_Momentum = Net()
net_RMSprop = Net()
net_Adam = Net()
nets = [net_SGD, net_Momentum, net_RMSprop, net_Adam]
3.8.3 优化器
接下来在创建不同的优化器, 用来训练不同的网络. 并创建一个 loss_func 用来计算误差. 我们用几种常见的优化器, SGD, Momentum, RMSprop, Adam.
代码如下:
# different optimizers
opt_SGD = torch.optim.SGD(net_SGD.parameters(), lr=LR)
opt_Momentum = torch.optim.SGD(net_Momentum.parameters(), lr=LR, momentum=0.8)
opt_RMSprop = torch.optim.RMSprop(net_RMSprop.parameters(), lr=LR, alpha=0.9)
opt_Adam = torch.optim.Adam(net_Adam.parameters(), lr=LR, betas=(0.9, 0.99))
optimizers = [opt_SGD, opt_Momentum, opt_RMSprop, opt_Adam]
loss_func = torch.nn.MSELoss()
losses_his = [[], [], [], []] # 记录 training 时不同神经网络的 loss
3.8.4train and show
代码如下:
# 训练
for epoch in range(EPOCH):
print('Epoch: ', epoch)
for step, (batch_x, batch_y) in enumerate(loader):
b_x = Variable(batch_x) # 务必要用 Variable 包一下
b_y = Variable(batch_y)
# 对每个优化器, 优化属于他的神经网络
for net, opt, l_his in zip(nets, optimizers, losses_his):
output = net(b_x) # get output for every net
loss = loss_func(output, b_y) # compute loss for every net
opt.zero_grad() # clear gradients for next train
loss.backward() # backpropagation, compute gradients
opt.step() # apply gradients
l_his.append(loss.data[0]) # loss recoder
# 出图
labels = ['SGD', 'Momentum', 'RMSprop', 'Adam']
for i, l_his in enumerate(losses_his):
plt.plot(l_his, label=labels[i])
plt.legend(loc='best')
plt.xlabel('Steps')
plt.ylabel('Loss')
plt.ylim((0, 0.2))
plt.show()
将以上代码合到一起执行结果:

SGD 是最普通的优化器, 也可以说没有加速效果, 而 Momentum 是 SGD 的改良版, 它加入了动量原则。后面的 RMSprop 又是 Momentum 的升级版,而 Adam 又是 RMSprop 的升级版. 不过从这个结果中我们看到, Adam 的效果似乎比 RMSprop 要差一点,所以说并不是越先进的优化器, 结果越佳。在自己的试验中可以尝试不同的优化器, 找到那个最适合你数据/网络的优化器。
此小节完整代码:在此
四、总结
通过几天的学习和敲代码的实践,中间出现了不少bug。想象与现实还是有一些差距的,希望自己以后能够多动手实践一下。基础课程看完了,接下来就是学习莫烦老师的高级课程了。希望自己能够记录自己的进步。










