【ZJOI 2015 幻想乡战略游戏】【动态点分治】

题意：求一棵树的带权重心，支持修改权值。

首先我们可以先用树分治构建出这棵树的分治树（不超过 logn 层），也就是把这棵树的重心作为根节点，然后子树为他的子树的重心这样递归下去，每个节点存的是其子树的信息，分别是 costfa[i]、cost[i]、dv[i]。
最后分治树中包了全部节点。

costfa[i] 是指 i 的子树到 fa[i] 的花费之和。
cost[i] 是指 i 的子树到 i 的花费之和。
dv[i] 是指 i 的子树的 dv 之和。

对于分治树的每一个点，我们枚举它的出边 e2[].y。
如果某条出边连向的点的距离之和小于当前点，那么答案一定在那条出边指向的子树中，用 e2[].to 分治做下去就行了。
如果不存在小于当前点的出边，那么当前点就是要找的重心。

e2[] 中 e2[].to 是对新建的分治树来说的，e2[].y 是对原树来说的。

从下往上更新信息
从上往下暴力查询更优节点，为什么我们不从下往上查询呢，因为我们记录的每个节点的信息是以子树为单位的

复杂度 O(nlog2n)

–

这里说一下怎么计算所有点到点 u 的贡献 cost

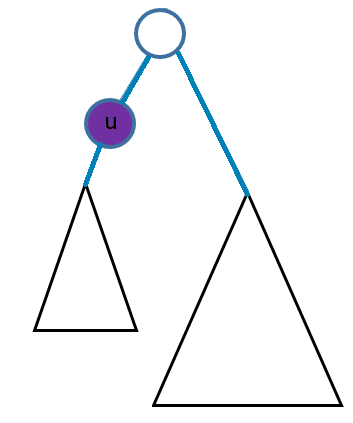
我们把 cost 分成三部分计算：u 子树对 u 的 cost 的部分我们可以之前预处理出来直接调用；剩余部分就从 u 往上计算一直不停的找 u 的 fa[i] 计算，具体实现我们分成两部分，以 u 为分界点，分别计算贡献。
cost=u子树对u的cost+fa[u]的除u子树以外的子树对fa[u]的cost+fa[u]的除u子树以外的子树从fa[u]到u的cost

fa[u] 的所有子树对 fa[u] 的 cost - u 子树对 fa[u] 的 cost

–

一定要开 long long 一定要！！！
为什么？？？
dv * dist(u, v) 在最坏情况下也就是一条链的情况下，会到 1e11 左右，答案应该是 1e16 左右。
（czq 这么说的！出锅找他！

我发现我是越来越菜了啊小 ly 已经帮我调不动题了 … 于是 czq 又帮我肝了一个小时啊 … (╯︵╰)

#include 
#define ll long long

using namespace std;
const ll N = 4e5 + 5;

struct Edge1 {
    ll to, next, w; 
}e1[N << 1];

struct Edge2 {
    ll to, next, y; // to 是对于新建的树来说的，y 是对于原树来说的 
}e2[N << 1];

ll cnt1 = 0, head1[N];
void add1(ll u, ll v, ll w) {
    e1[++ cnt1].to = v; e1[cnt1].w = w; e1[cnt1].next = head1[u]; head1[u] = cnt1;
}

int cnt2 = 0, head2[N];
void add2(ll u, ll v, ll y) {
    e2[++ cnt2].to = v; e2[cnt2].y = y; e2[cnt2].next = head2[u]; head2[u] = cnt2;
}

ll dep[N], fa[N], hson[N], size[N], dis[N];
void dfs1(ll u, ll f, ll depth) {
    fa[u] = f;
    dep[u] = depth;
    size[u] = 1;
    for (ll i = head1[u]; i; i = e1[i].next) {
        int v = e1[i].to;
        if (v == f) continue;
        dis[v] = dis[u] + e1[i].w;
        dfs1(v, u, depth + 1);
        size[u] += size[v];
        if (hson[u] == -1 || size[hson[u]] < size[v]) hson[u] = v;
    }
}

ll top[N];
void dfs2(ll u, ll tp) {
    top[u] = tp;
    if (hson[u] == -1) return ;
    dfs2(hson[u], tp);
    for (ll i = head1[u]; i; i = e1[i].next) {
        ll v = e1[i].to;
        if (v != fa[u] && v != hson[u]) dfs2(v, v); 
    }
}

inline ll lca(ll a, ll b) {
    while (top[a] != top[b]) {
        if (dep[top[a]] > dep[top[b]]) a = fa[top[a]];
        else b = fa[top[b]];    
    }
    return (dep[a] < dep[b]) ? a : b;
}

inline ll getdis(ll x, ll y) {
    return (dis[x] + dis[y]) - 2 * dis[lca(x, y)];
}

struct DF_tree {
    ll sum, rt;
    ll cost[N], costfa[N], dv[N]; 

    ll son[N], size[N], vis[N];
    void getrt(ll u, ll f) {
        son[u] = 1;
        size[u] = 0;

        for (ll i = head1[u]; i; i = e1[i].next) {
            ll v = e1[i].to;
            if (v == f || vis[v]) continue;
            getrt(v, u);
            son[u] += son[v];
            size[u] = max(size[u], son[v]);
        }

        size[u] = max(size[u], sum - son[u]);
        if (size[u] < size[rt]) rt = u;
    }

    ll fa[N];
    void solve(ll u, ll f) {
        vis[u] = 1; fa[u] = f;
        for (ll i = head1[u]; i; i = e1[i].next) {
            ll v = e1[i].to;
            if (vis[v]) continue;
            sum = size[0] = son[v];
            getrt(v, rt = 0); add2(u, rt, v);
            solve(rt, u);
        }
    }

    void change(ll u, ll val) { // 从下往上更新信息
        dv[u] += val;
        for (ll i = u; fa[i]; i = fa[i]) {
            ll disnum = getdis(u, fa[i]);
            cost[fa[i]] += disnum * val;
            costfa[i] += disnum * val;
            dv[fa[i]] += val;   
        }
    }

    ll cal(int u) {
        ll ans = cost[u];
        for (ll i = u; fa[i]; i = fa[i]) {
            ll disnum = getdis(u, fa[i]);
            ans += cost[fa[i]] - costfa[i];
            ans += disnum * (dv[fa[i]] - dv[i]);
        }
        return ans;
    }

    ll query(int u) { // 从上往下暴力查询更优节点，为什么我们不从下往上查询呢，因为我们记录的每个节点的信息是以子树为单位的
        ll res = cal(u);
        for (ll i = head2[u]; i; i = e2[i].next) {
            ll v = e2[i].to, y = e2[i].y;
            ll tem = cal(y);
            if (tem < res) return query(v);
        }
        return res;
    }
}dftree;

int main() {
    memset(hson, -1, sizeof(hson));
    memset(dftree.vis, 0, sizeof(dftree.vis));

    ll oldrt;
    ll n, m;
    scanf("%lld%lld", &n, &m);
    for (ll i = 1; i < n; i ++) {
        ll x, y, z;
        scanf("%lld%lld%lld", &x, &y, &z);
        add1(x, y, z), add1(y, x, z);
    }

    dftree.sum = dftree.size[0] = n;
    dftree.getrt(1, 0);
    oldrt = dftree.rt;
    dfs1(dftree.rt, 0, 0); dfs2(dftree.rt, dftree.rt);
    dftree.solve(dftree.rt, 0);

    for (ll i = 1; i <= m; i ++) {
        ll u, val;
        scanf("%lld%lld", &u, &val);
        dftree.change(u, val);
        printf("%lld\n", dftree.query(oldrt));
    }
    return 0;   
}