多项式全家桶——Part.1 多项式加减乘
多项式全家桶它lei了。
好吧,最近发现自己的多项式芝士严重匮乏,发现只会FFT和NTT,而且还有点生疏。
那既然没事干,那就来吃吃全家桶来补充芝士储备。
多项式
多项式是一个神奇的东东。
它长这样: ∑ i = 0 n − 1 a i x i \sum_{i=0}^{n-1} a_ix^i ∑i=0n−1aixi
好的,讲完了。
多项式加法、减法
由于多项式长这样: ∑ a i x i \sum a_ix^i ∑aixi
那么假设这两个多项式相加、减: ∑ a i x i 、 ∑ b i x i \sum a_ix^i、\sum b_ix^i ∑aixi、∑bixi
那么结论就是: ∑ ( a i ± b i ) x i \sum (a_i\pm b_i)x^i ∑(ai±bi)xi
多项式乘法
这玩意长这样: ( 1 + a 1 x + a 2 x 2 + … + a n − 1 x n − 1 ) ( 1 + b 1 x + b 2 x 2 + … + b m − 1 x m − 1 ) (1+a_1x+a_2x^2+…+a_{n-1}x^{n-1})(1+b_1x+b_2x^2+…+b_{m-1}x^{m-1}) (1+a1x+a2x2+…+an−1xn−1)(1+b1x+b2x2+…+bm−1xm−1)
两个多项式相乘就叫做多项式乘法。
具体做法有三种,FFT、NTT 和 MTT
超强wd的博客有讲FFT
这玩意我们直接暴力求是 O ( n 2 ) O(n^2) O(n2)的。
然后就出现了两个低级算法:DFT和IDFT
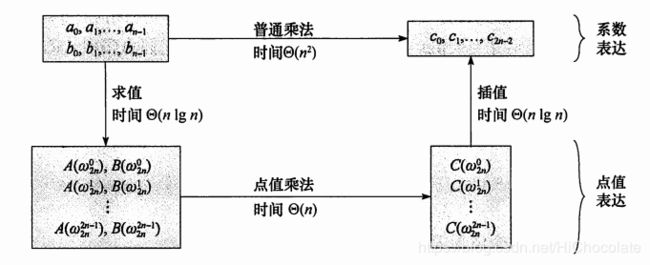
DFT、IDFT
DFT叫做离散傅里叶变换,IDFT则是离散傅里叶逆变换。
DFT就是将系数表示法转成点值表示法。
IDFT则是反过来。
有什么好处呢?转成点值后:
A = ( x 1 , A ( x 1 ) ) ( x 2 , A ( x 2 ) ) ( x 3 , A ( x 3 ) ) … … ( x n − 1 , A ( x n − 1 ) ) A=(x_1,A(x_1))(x_2,A(x_2))(x_3,A(x_3))……(x_{n-1},A(x_{n-1})) A=(x1,A(x1))(x2,A(x2))(x3,A(x3))……(xn−1,A(xn−1))
B = ( x 1 , B ( x 1 ) ) ( x 2 , B ( x 2 ) ) ( x 3 , B ( x 3 ) ) … … ( x n − 1 , B ( x n − 1 ) ) B=(x_1,B(x_1))(x_2,B(x_2))(x_3,B(x_3))……(x_{n-1},B(x_{n-1})) B=(x1,B(x1))(x2,B(x2))(x3,B(x3))……(xn−1,B(xn−1))
那么乘起来就是:
A ∗ B = ( x 1 , A ( x 1 ) ∗ B ( x 1 ) ) ( x 2 , A ( x 2 ) ∗ B ( x 2 ) ) ( x 3 , A ( x 3 ) ∗ B ( x 3 ) ) … … ( x n − 1 , A ( x n − 1 ) ∗ B ( x n − 1 ) ) A*B=(x_1,A(x_1)*B(x_1))(x_2,A(x_2)*B(x_2))(x_3,A(x_3)*B(x_3))……(x_{n-1},A(x_{n-1})*B(x_{n-1})) A∗B=(x1,A(x1)∗B(x1))(x2,A(x2)∗B(x2))(x3,A(x3)∗B(x3))……(xn−1,A(xn−1)∗B(xn−1))
这样我们可以在 O ( n ) O(n) O(n)时间内做出。
然鹅朴素的DFT和IDFT还是 O ( n 2 ) O(n^2) O(n2)的,那么超级算法FFT就是用来优化之的。
FFT
单位根的性质Copy我那个被吃掉的博客:
———————————————————————————————————
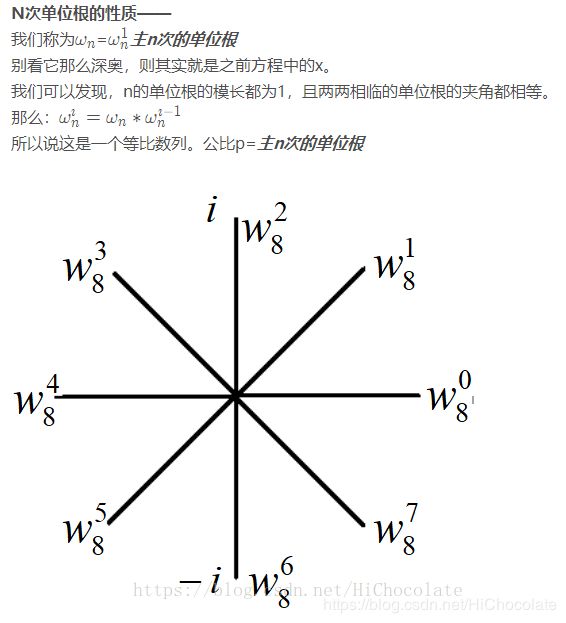
1、 ω n n = ω n 0 = 1 \omega_n^n=\omega_n^0=1 ωnn=ωn0=1
2、 ω n x ω n y = ω n x + y = ω n ( x + y ) m o d n \omega_n^x\omega_n^y=\omega_n^{x+y}=\omega_n^{(x+y)mod n} ωnxωny=ωnx+y=ωn(x+y)modn
因为两个相乘就相当于两个相加(显然),然后就相当于旋转了(x+y)次。如果mod一下,那么就相当于转了很多圈回到了原来的一个值。
3、 ω n x = ω n n + x \omega_n^x=\omega_n^{n+x} ωnx=ωnn+x
证明与上面的一样。
4、群的性质:满足 ω n x < > ω n y \omega_n^x<>\omega_n^y ωnx<>ωny当且仅当x mod n<>y mod n
5、消去引理: ω d n d x = ω n x \omega_{dn}^{dx}=\omega_n^x ωdndx=ωnx
6、折半引理: ( ω n i ) 2 = ( ω n i + n 2 ) 2 = ω n 2 i ( 当 2 ∣ n 时 ) ({\omega_n^i})^2=(\omega_n^{i+ \frac n2 })^2=\omega_n^{2i} (当2|n时) (ωni)2=(ωni+2n)2=ωn2i(当2∣n时)
证明:
∵ ( ω n i ) 2 = ω n 2 i \because({\omega_n^i})^2=\omega_n^{2i} ∵(ωni)2=ωn2i
∵ ω n 2 i = ω n 2 i + n = ( ω n i + n 2 ) 2 \because\omega_n^{2i}=\omega_n^{2i+n}=(\omega_n^{i+ \frac n2 })^2 ∵ωn2i=ωn2i+n=(ωni+2n)2
∴ ( ω n i ) 2 = ( ω n i + n 2 ) 2 \therefore({\omega_n^i})^2=(\omega_n^{i+ \frac n2 })^2 ∴(ωni)2=(ωni+2n)2
事实上: ω n i = − ω n i + n 2 \omega_n^i=-\omega_n^{i+ \frac n2 } ωni=−ωni+2n
很好理解恩?
7、求和引理: 对于任意正整数n和非负整数k,且n不是k的倍数时,满足: ∑ i = 0 n − 1 ( ω n k ) i = 0 \sum_{i=0}^{n-1}(\omega^k_n)^i=0 ∑i=0n−1(ωnk)i=0
证明:
运用等比数列:
∑ i = 0 n − 1 ( ω n k ) i = 1 − ( ω n k ) n 1 − ω n k = 1 − ( ω n n ) k 1 − ω n k = 1 − 1 k 1 − ω n k = 0 \sum_{i=0}^{n-1}(\omega^k_n)^i=\frac{1-(\omega_n^k)^n}{1-\omega_n^k}=\frac{1-(\omega_n^n)^k}{1-\omega_n^k}=\frac{1-1^k}{1-\omega_n^k}=0 i=0∑n−1(ωnk)i=1−ωnk1−(ωnk)n=1−ωnk1−(ωnn)k=1−ωnk1−1k=0
8、不知道什么引理或定理:
ω n k + n 2 = − ω n k \omega_n^{k+\frac n2}=-\omega_n^k ωnk+2n=−ωnk
———————————————————————————————————
现在我们知道了单位根的性质了。
然后我们康康FFT怎么来用单位根的性质来加速。
A ( x ) = ∑ i = 0 n − 1 a i ∗ x i = a 0 ∗ x 0 + a 1 ∗ x 1 + a 2 ∗ x 2 + … … + a n − 1 ∗ x n − 1 A(x)=\sum_{i=0}^{n-1}a_i*x^i=a_0*x^0+a_1*x^1+a_2*x^2+……+a_{n-1}*x^{n-1} A(x)=i=0∑n−1ai∗xi=a0∗x0+a1∗x1+a2∗x2+……+an−1∗xn−1
我们把这个玩意按照下标奇偶性来分个类。
= ( a 0 ∗ x 0 + a 2 ∗ x 2 + … … + a n − 2 ∗ x n − 2 ) + ( a 1 ∗ x 1 + a 3 ∗ x 3 + … … + a n − 1 ∗ x n − 1 ) = ( a 0 ∗ x 0 + a 2 ∗ x 2 + … … + a n − 2 ∗ x n − 2 ) + x ∗ ( a 1 ∗ x 0 + a 3 ∗ x 2 + … … + a n − 1 ∗ x n − 2 ) =(a_0*x^0+a_2*x^2+……+a_{n-2}*x^{n-2})+(a_1*x^1+a_3*x^3+……+a_{n-1}*x^{n-1}) \\=(a_0*x^0+a_2*x^2+……+a_{n-2}*x^{n-2})+x*(a_1*x^0+a_3*x^2+……+a_{n-1}*x^{n-2}) =(a0∗x0+a2∗x2+……+an−2∗xn−2)+(a1∗x1+a3∗x3+……+an−1∗xn−1)=(a0∗x0+a2∗x2+……+an−2∗xn−2)+x∗(a1∗x0+a3∗x2+……+an−1∗xn−2)
设
A 1 ( x ) = a 0 ∗ x 0 + a 2 ∗ x + a 4 ∗ x 2 + … … + a n − 2 ∗ x n − 2 2 A 2 ( x ) = a 1 ∗ x 0 + a 3 ∗ x + a 5 ∗ x 2 … … + a n − 1 ∗ x n − 2 2 A1(x)=a_0*x^0+a_2*x+a_4*x^2+……+a_{n-2}*x^\frac{n-2}2\\A2(x)=a_1*x^0+a_3*x+a_5*x^2……+a_{n-1}*x^\frac{n-2}2 A1(x)=a0∗x0+a2∗x+a4∗x2+……+an−2∗x2n−2A2(x)=a1∗x0+a3∗x+a5∗x2……+an−1∗x2n−2
则
A ( x ) = A 1 ( x 2 ) + x ∗ A 2 ( x 2 ) A(x)=A1(x^2)+x*A2(x^2) A(x)=A1(x2)+x∗A2(x2)
接下来我们开始利用单位根了!

设 k < = n 2 k<=\frac n 2 k<=2n,然后把 ω n k \omega_n^k ωnk当做 x x x代入得到:
A ( ω n k ) = A 1 ( ( ω n k ) 2 ) + ω n k ∗ A 2 ( ( ω n k ) 2 ) A(\omega_n^k)=A1((\omega_n^k)^2)+\omega_n^k*A2((\omega_n^k)^2) A(ωnk)=A1((ωnk)2)+ωnk∗A2((ωnk)2)
根据折半引理:
A ( ω n k ) = A 1 ( ω n 2 k ) + ω n k ∗ A 2 ( ω n 2 k ) A(\omega_n^k)=A1(\omega_n^{2k})+\omega_n^k*A2(\omega_n^{2k}) A(ωnk)=A1(ωn2k)+ωnk∗A2(ωn2k)
根据消去引理:
A ( ω n k ) = A 1 ( ω n 2 k ) + ω n k ∗ A 2 ( ω n 2 k ) A(\omega_n^k)=A1(\omega_\frac n2^k)+\omega_n^k*A2(\omega_\frac n2^k) A(ωnk)=A1(ω2nk)+ωnk∗A2(ω2nk)
然后再把 ω n k + n 2 \omega_n^{k+\frac n 2} ωnk+2n代入得到
A ( ω n k + n 2 ) = A 1 ( ( ω n k + n 2 ) 2 ) + ω n k + n 2 ∗ A 2 ( ( ω n k + n 2 ) 2 ) = A 1 ( ω n 2 k + n ) − ω n k ∗ A 2 ( ω n 2 k + n ) = A 1 ( ω n 2 k ) − ω n k ∗ A 2 ( ω n 2 k ) = A 1 ( ω n 2 k ) − ω n k ∗ A 2 ( ω n 2 k ) A(\omega_n^{k+\frac n 2}) =A1((\omega_n^{k+\frac n 2})^2)+\omega_n^{k+\frac n 2}*A2((\omega_n^{k+\frac n 2})^2) \\=A1(\omega_n^{2k+n})-\omega_n^k*A2(\omega_n^{2k+n}) \\=A1(\omega_n^{2k})-\omega_n^k*A2(\omega_n^{2k}) \\=A1(\omega_\frac n2^k)-\omega_n^k*A2(\omega_\frac n2^k) A(ωnk+2n)=A1((ωnk+2n)2)+ωnk+2n∗A2((ωnk+2n)2)=A1(ωn2k+n)−ωnk∗A2(ωn2k+n)=A1(ωn2k)−ωnk∗A2(ωn2k)=A1(ω2nk)−ωnk∗A2(ω2nk)
继而发现,上面两坨玩意儿只有一个符号变了。
意味着,求出 A 1 ( ω n 2 k ) A1(\omega_\frac n2^k) A1(ω2nk)和 A 2 ( ω n 2 k ) A2(\omega_\frac n2^k) A2(ω2nk)的答案,即可求出 A ( ω n k ) A(\omega_n^k) A(ωnk)与 A ( ω n k + n 2 ) A(\omega_n^{k+\frac n 2}) A(ωnk+2n)
于是我们就可以很开心地分治了。
由于分治的常数极大,所以我这里就不贴代码了。
下面有个神奇的优化可以完善之。
IFFT
前面加了个I的东东都是原来的东东的逆运算。
所以IFFT就是将点值转为插值的算法。
哦,点值转插值,这个我会。不就是拉格朗日插值吗?
那你可去试试
反正这玩意可以有多种方法来表示,什么矩阵,什么奇怪的推柿子。
然鹅我都不肥。
那就记住结论闯天下了。
- fft过程中乘上共轭复数,然后做完后再除以n就是插值了。
证明别找我。
蝴蝶变化
迭代大法:

于是我们发现:
每个下标的二进制形式反过来就是它们最后在序列中的位置。
于是直接rush。
#include 学习资料:
百度百科
https://www.cnblogs.com/Chandery/p/11332777.html
https://blog.csdn.net/YY_Tina/article/details/88361459
https://blog.csdn.net/enjoy_pascal/article/details/81478582
https://www.cnblogs.com/zwfymqz/p/8244902.html#_label4
NTT
直接看这个了,自我感觉写得还阔以
#include MTT
这什么毒瘤东东。
放放,有时间再学吧
ColdChair大爷