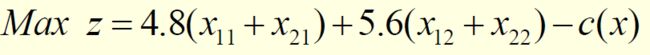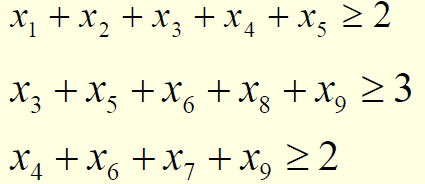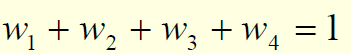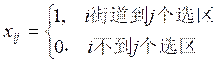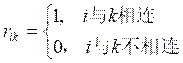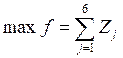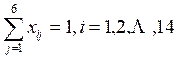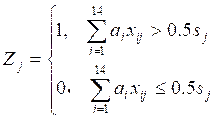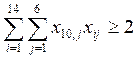数学建模之常见的优化模型
EverydayOneCat
肝ing

知识点
1.运输问题
前面线性规划文章中已经讲过经典的运输问题。这个例子只是一个补充,在考虑经济效益的基础上进行运输问题的研究。
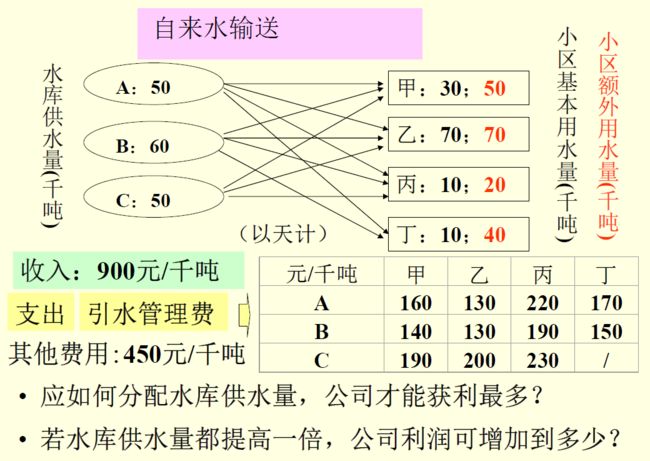
建立模型:
ai:第i个水库供水量
bi:第i个小区基本用水量
ci:第i个小区额外用水量
dij:从第i歌水库运到第j个小区的管理费
决策变量:xij:从第i个水库运到第j个小区的水量
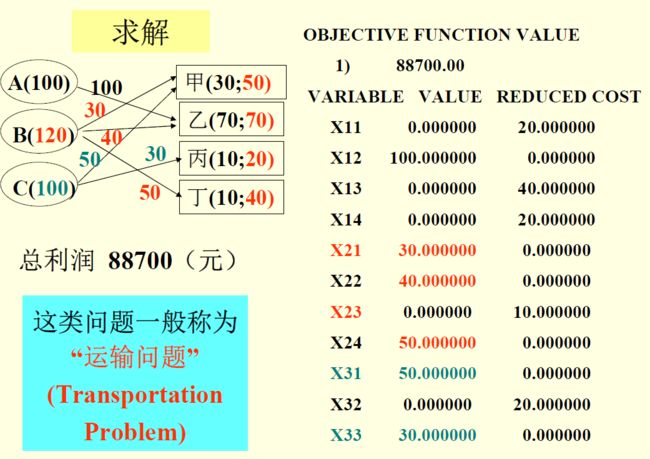
m a x Z = ∑ i = 1 3 ∑ j = 1 4 x i j s t d : { x 34 = 0 , ∑ j = 1 4 x i j ≤ a i , i=1,2,3 ∑ i = 1 3 x i j ≥ b j , j=1,2,3,4 ∑ j = 1 4 x i j ≤ c j + b j , j=1,2,3,4 maxZ=\sum_{i=1}^{3}\sum_{j=1}^{4}{x_{ij}}\\ std: \begin{cases} x_{34}=0, & \text{} \\ \sum_{j=1}^{4}{x_{ij}}\leq a_i, & \text{i=1,2,3}\\ \sum_{i=1}^{3}{x_{ij}}\ge b_j, & \text{j=1,2,3,4}\\ \sum_{j=1}^{4}{x_{ij}}\le c_j+b_j, & \text{j=1,2,3,4} \end{cases} maxZ=i=1∑3j=1∑4xijstd:⎩⎪⎪⎪⎨⎪⎪⎪⎧x34=0,∑j=14xij≤ai,∑i=13xij≥bj,∑j=14xij≤cj+bj,i=1,2,3j=1,2,3,4j=1,2,3,4

供水量提高一倍模型一样,修改一下数据即可。
2.装箱问题
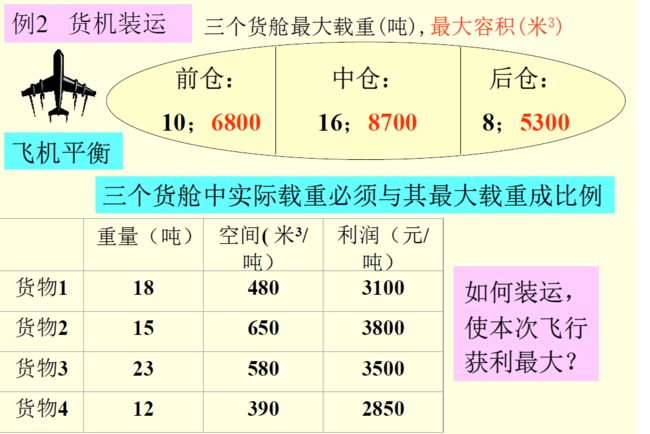
这道题建模主要难点在于三个货舱中实际载重必须与其最大载重成比例。其实解决方法很简单,我们把他们都比上比例的值相等即可。
模型假设:
每种货物可以分割到任意小;
每种货物可以在一个或多个货舱中任意分布;
多种货物可以混装,并保证不留空隙;
ai:第i个货舱最大载重
bi:第i个货舱最大容积
cj:第j个货物的最大重量
dj:第j个货物的空间
ej:第j个货物的利润
T:常数
决策变量:xij:第i个前舱放货物j的重量
m a x Z = ∑ i = 1 3 ∑ j = 1 4 x i j ∗ e j s t d : { ∑ j = 1 4 x i j a i = T , i=1,2,3 ∑ i = 1 3 x i j ≤ c j , j=1,2,3,4 ∑ j = 1 4 x i j ∗ d j ≤ b i , i=1,2,3 ∑ j = 1 4 x i j ≤ a i , i=1,2,3 maxZ=\sum_{i=1}^{3}\sum_{j=1}^{4}{x_{ij}*e_{j}}\\ std: \begin{cases} \frac{\sum_{j=1}^{4}{x_{ij}}}{a_i}=T, & \text{i=1,2,3}\\ \sum_{i=1}^{3}{x_{ij}}\le c_j, & \text{j=1,2,3,4}\\ \sum_{j=1}^{4}{x_{ij}*d_j}\leq b_i, & \text{i=1,2,3}\\ \sum_{j=1}^{4}{x_{ij}}\le a_i, & \text{i=1,2,3} \end{cases} maxZ=i=1∑3j=1∑4xij∗ejstd:⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧ai∑j=14xij=T,∑i=13xij≤cj,∑j=14xij∗dj≤bi,∑j=14xij≤ai,i=1,2,3j=1,2,3,4i=1,2,3i=1,2,3
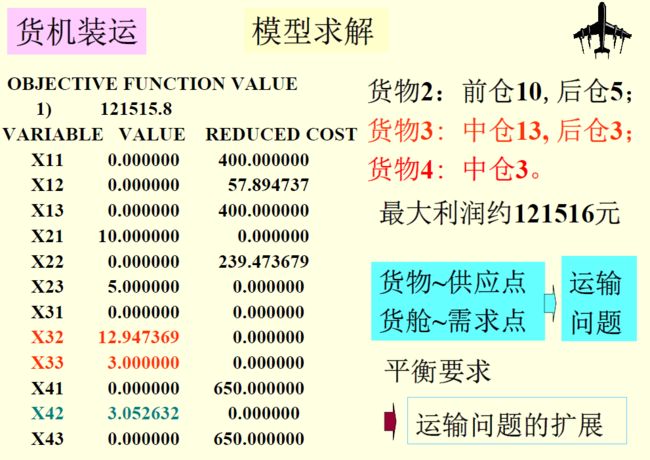
3.生产计划问题
汽车厂生产三种类型的汽车,已知各类型每辆车对钢材、劳动时间的需求,利润及工厂每月的现有量。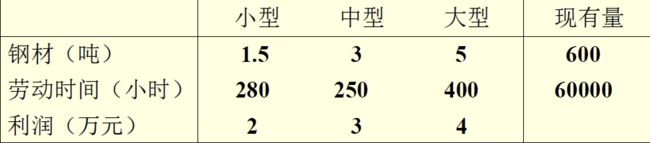
(1)制订月生产计划,使工厂的利润最大。
(2)如果生产某一类型汽车,则至少要生产80辆,那么最优的生产计划应作何改变?
第一问很简单,普通的建立线性规划模型即可:
设每月生产小、中、大型汽车的数量分别为x1, x2, x3
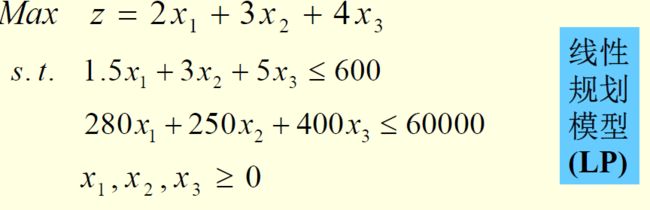
这里有个需要注意的小细节,一般通常数据量较小的时候,我们可以通过整数规划来求解(因为汽车数量没有小数一说),但是一旦数据量较大,我们就需要去掉整数的条件来使得运算更加快速。具体方法我们通过本例来讲述:

1)舍去小数:取x1=64,x2=167,算出目标函数值z=629,与LP最优值632.2581相差不大。
2)试探:如取x1=65,x2=167;x1=64,x2=168等,计算函数值z,通过比较可能得到更优的解。
• 但必须检验它们是否满足约束条件。
+++
第二问:若生产某类汽车,则至少生产80辆,我们可以得到条件x1,x2, x3=0 或>=80
方法1:分解为8个LP子模型
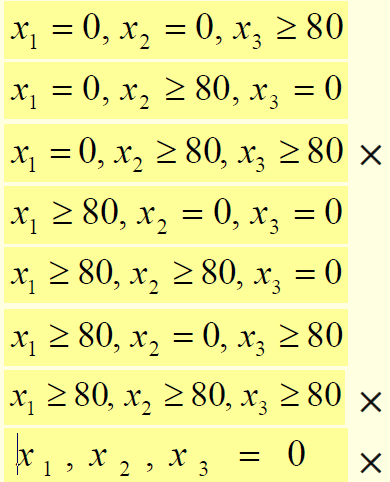
x1=80,x2= 150,x3=0,最优值z=610
方法2:引入0-1变量,化为整数规划


方法3:化为非线性规划

非线性规划(Non- Linear Programming,简记NLP)虽然可用现成的数学软件求解( 如LINGO,MATLAB),但是其结果常依赖于初值的选择。
4.分段函数问题
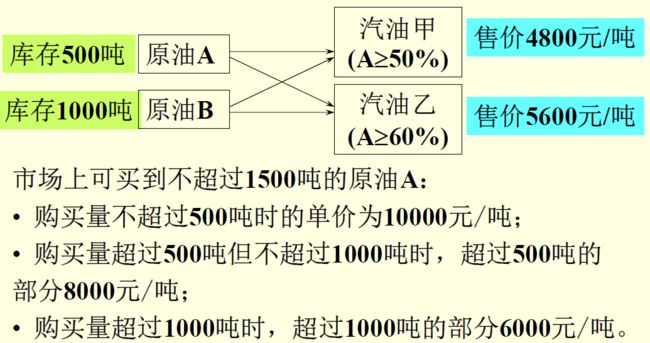

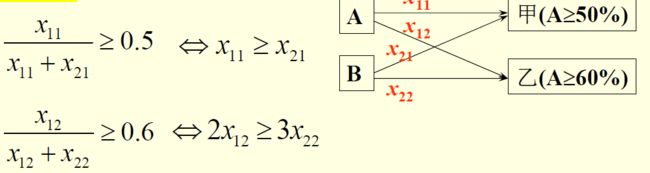
对于用分段函数定义的c(x),一般的非线性规划软件也难以输入和求解,得想办法将模型化简。
+++
方法一:相乘
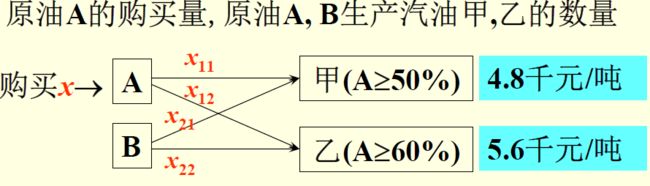
x1 , x2 , x3 ~以价格10, 8, 6(千元/吨)采购A的吨数,x~购买A的总吨数
x1到达500,x2才能不为0,也就是x1=500或者x2=0,遇到这种或问题,想到相乘;x3同理
x= x1+x2+x3, c(x) = 10x1+8x2+6x3

非线性规划模型,可以用LINGO求解
Model:
Max= 4.8*x11 + 4.8*x21 + 5.6*x12 + 5.6*x22 - 10*x1 - 8*x2 - 6*x3;
x11+x12 < x + 500;
x21+x22 < 1000;
x11 - x21 > 0;
2*x12 - 3*x22 > 0;
x=x1+x2+x3;
(x1 - 500) * x2=0;
(x2 - 500) * x3=0;
x1 < 500;
x2 < 500;
x3 < 500;
x > 0;
x11 > 0;
x12 > 0;
x21 > 0;
x22 > 0;
x1 > 0;
x2 > 0;
x3 > 0;
end

+++
方法二:转化为整数规划
y1, y2 , y3=1 ~以价格10, 8, 6(千元/吨)采购A
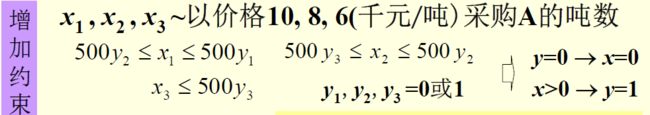
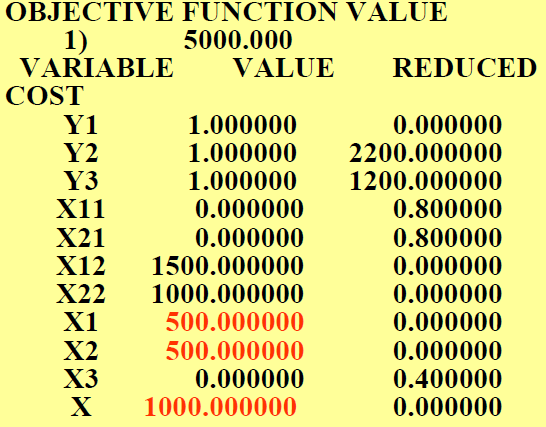
购买1000吨原油A,与库存的500吨原油A和1000吨原油B一起,生产汽油乙,利润为5,000千元。优于方法1的结果
+++
这里还有方法三:直接处理处理分段线性函数c(x)
这一段看了一遍没看懂,不高兴研究了。其实懂得方法一二已经足够用了,这里我直接照搬。看懂的xdm把流弊打在公屏上。

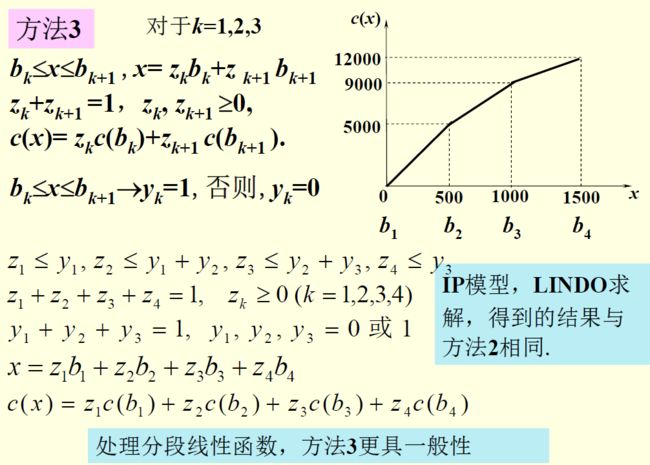
5.分派问题
选课策略:要求至少选两门数学课、三门运筹学课和两门计算机课
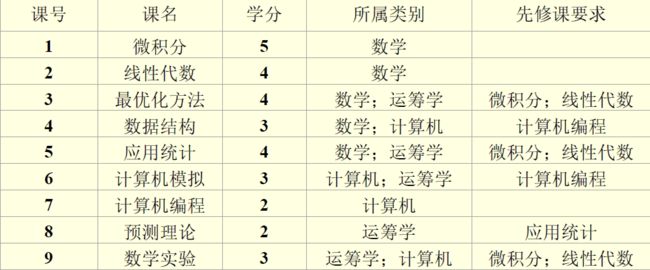
(1)为了选修课程门数最少,应学习哪些课程?
(2)选修课程最少,且学分尽量多,应学习哪些课程?
第一问:
选或者不选我们想到0-1规划模型
决策变量:xi=1 ~选修课号i 的课程(xi=0 ~不选)

第二问:多目标规划


6.饮料厂的生产与检修计划
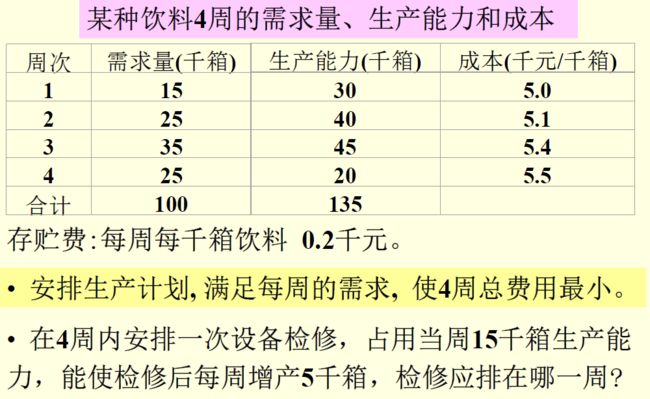
第一问:
模型假设:
• 饮料厂在第1周开始时没有库存;
• 从费用最小考虑, 第4周末不能有库存;
• 周末有库存时需支出一周的存贮费;
• 每周末的库存量等于下周初的库存量。
决策变量:
x1~ x4:第1~4周的生产量
y1~ y3:第1~3周末库存量
约束条件:

接着到了本题重点第二问:
检修安排在任一周均可,所以这四周分为检修和不检修,导入0-1变量。0-1变量wt :wt=1~ 检修安排在第t周(t=1,2,3,4)
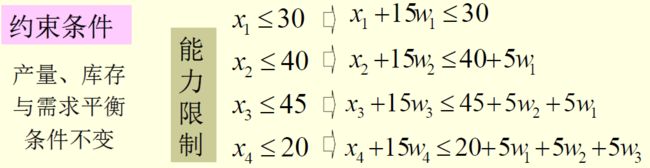
作业
题目:选区划分
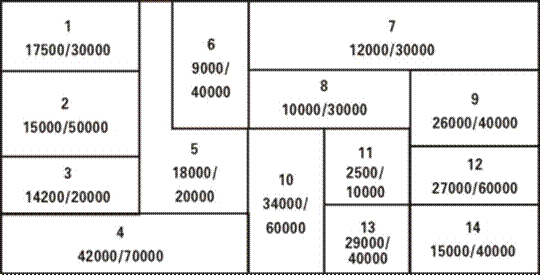
在—个遥远的国家,Sark Mevo 所领导的政党最终击败了Reguel Tekris王子领导的联合党派。Mevo希望巩固他在首都地区的席位。首都由14个街区组成,这些街区将分组为多个选区。下图是首都地区的示意图。在图中用数字1到14对这些街区进行了编号。每个街区中的另外两个数字是预计该街区会投票给Mevo的选民数和该街区的选民总数。所有选民都必须投票,且选举胜出方必须得到绝对多数选票。一个选区可以由多个相邻的街区组成,且选区内总选民数应在30,000到100,000之间。如果两个街区不相邻,例如12和13,则它们不能组成一个选区。如果某个街区选民人数不少于50,000,则允许此街区单独作为一个选区。但是由于Mevo本人就居住在街区10内,因此迫于舆论压力,他不能将这个街区单独作为一个选区。
请设计出一个将首都划分为5个选区的方案,以使Mevo得到的席位数最多。如果这样做有困难,可以尝试划分为6个选区。
分析
经核算首都共有54万人,而每个选区至多10000人,所以五个选区是不行的,要划分成六个选区。
![]() 第i街区Mevo派选民,
第i街区Mevo派选民,![]() 第i街区总人数
第i街区总人数
目标函数:希望获得席位数最多
约束一:每个街道必须并入一个选区
约束二:满足选区人数要求,单位:单位:百人
约束三:胜利和失败的条件
约束四:选区中街道之间必须关联。
当![]() 时,
时,![]()
约束五:第10个街区不能单独成选区。因为第10行只有一个数为1(约束一的规定),现在就要求这一列还有别的![]() 为1,两者相乘为1。因为不想用过滤条件,自己和自己相乘为1.
为1,两者相乘为1。因为不想用过滤条件,自己和自己相乘为1.
即![]() 。所以就定义下列约束条件。
。所以就定义下列约束条件。
约束六:第i个街区单独成选区的条件是人数大于5万
约束七 缩小迭代次数,规定人数最多的选取下标为1,以此类推。
![]()
最后就是0-1和整数约束了
代码
根据上面分析的模型编写lingo代码:
model:
sets:
jq/1..14/:a,b;
xq/1..6/:z,s,bili;
link1(jq,xq):x;
link2(jq,jq):r;
endsets
data:
a=175 150 142 420 180 90 120 100 260 340 25 270 290 150;
b=300 500 200 700 200 400 300 300 400 600 100 600 400 400;
r=1 1 0 0 1 0 0 0 0 0 0 0 0 0
1 1 1 0 1 0 0 0 0 0 0 0 0 0
0 1 1 1 1 0 0 0 0 0 0 0 0 0
0 0 1 1 1 0 0 0 0 1 0 0 0 0
1 1 1 1 1 1 0 0 0 1 0 0 0 0
0 0 0 0 1 1 1 1 0 0 0 0 0 0
0 0 0 0 0 1 1 1 1 0 0 0 0 0
0 0 0 0 0 1 1 1 1 1 1 0 0 0
0 0 0 0 0 0 1 1 1 0 1 1 0 0
0 0 0 1 1 0 0 1 0 1 1 0 1 0
0 0 0 0 0 0 0 1 1 1 1 1 1 0
0 0 0 0 0 0 0 0 1 0 1 1 0 1
0 0 0 0 0 0 0 0 0 1 1 0 1 1
0 0 0 0 0 0 0 0 0 0 0 1 1 1;
enddata
max=@sum(xq:z);
@for(jq(i):@sum(xq(j):x(i,j))=1);
@for(xq(j):s(j)=@sum(jq(i):b(i)*x(i,j)));
@for(xq:s<1000;s>300);
@for(xq(j):z(j)=@if(@sum(jq(i):a(i)*x(i,j))#gt#0.5*s(j),1,0));
@for(xq(j):@for(link2(i,k)|i#ne#k:x(i,j)+x(k,j)<@if(r(i,k)#eq#0,1,x(i,j)+x(k,j))));
@sum(link1(i,j):x(10,j)*x(i,j))>2;
@for(xq(j):s(j)>@if(@sum(jq(i):x(i,j))#eq#1,500,s(j)));
@for(link1:@bin(x));
@for(xq(j):bili=@sum(jq(i):a(i)*x(i,j))/s(j));
end
根据结果可知席数最多为5个选区。
结语
我妈嫌占空间把从小陪到大的台式机给卖给收废品的了,真的吐了NMD就值50
很烦,最近不想学了