图优化算法（2）_利用gtsam库完成因子图优化

这两天在学习gtsam库，这里参考网站内容作了简单图优化测试。
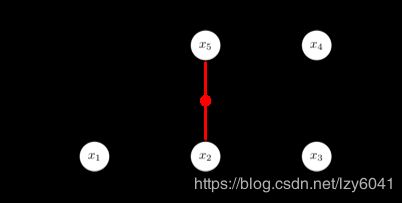
图示：
这是官网的一个2D位姿图优化示例，大概是这样一个意思，一共右5个站点，首先机器人从x1点，朝同一方向经过x2,x3，然后x3站点旋转90度到达站点x4，再然后站点4再经90度旋转到达x5点， x再旋转90度发现”这个地方好像来过“——通过x2,x5之间建立约束关系。
ps:机器人底盘里程计计算在每两个站点间距离均为5m，实际上并没有5m，每个站点实际到达可能要差一点儿，那么累积误差就比较大了，这也是为什么要回环检测，然后作图优化的原因。

源代码：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
using namespace gtsam;
int main(int argc, char** argv) 
{
    NonlinearFactorGraph graph;

    Values initials;
    initials.insert(Symbol('x', 1), Pose2(0.2, -0.3, 0.2));
    initials.insert(Symbol('x', 2), Pose2(5.1, 0.3, -0.1));
    initials.insert(Symbol('x', 3), Pose2(9.9, -0.1, -M_PI_2 - 0.2));
    initials.insert(Symbol('x', 4), Pose2(10.2, -5.0, -M_PI + 0.1));
    initials.insert(Symbol('x', 5), Pose2(5.1, -5.1, M_PI_2 - 0.1));
    initials.print("\nInitial Values:\n"); 
    //固定第一个顶点，在gtsam中相当于添加一个先验因子
    noiseModel::Diagonal::shared_ptr priorModel = noiseModel::Diagonal::Sigmas(Vector3(1.0, 1.0, 0.1));
    graph.add(PriorFactor<Pose2>(Symbol('x', 1), Pose2(0, 0, 0), priorModel));

    //二元位姿因子
    noiseModel::Diagonal::shared_ptr odomModel = noiseModel::Diagonal::Sigmas(Vector3(0.5, 0.5, 0.1));
    graph.add(BetweenFactor<Pose2>(Symbol('x', 1), Symbol('x', 2), Pose2(5, 0, 0), odomModel));
    graph.add(BetweenFactor<Pose2>(Symbol('x', 2), Symbol('x', 3), Pose2(5, 0, -M_PI_2), odomModel));
    graph.add(BetweenFactor<Pose2>(Symbol('x', 3), Symbol('x', 4), Pose2(5, 0, -M_PI_2), odomModel));
    graph.add(BetweenFactor<Pose2>(Symbol('x', 4), Symbol('x', 5), Pose2(5, 0, -M_PI_2), odomModel));

    //二元回环因子
    noiseModel::Diagonal::shared_ptr loopModel = noiseModel::Diagonal::Sigmas(Vector3(0.5, 0.5, 0.1));
    graph.add(BetweenFactor<Pose2>(Symbol('x', 5), Symbol('x', 2), Pose2(5, 0, -M_PI_2), loopModel));
    graph.print("\nFactor Graph:\n"); 


    GaussNewtonParams parameters;
    parameters.setVerbosity("ERROR");
    parameters.setMaxIterations(20);
    parameters.setLinearSolverType("MULTIFRONTAL_QR");
    GaussNewtonOptimizer optimizer(graph, initials, parameters);
    Values results = optimizer.optimize();
    results.print("Final Result:\n");

    Marginals marginals(graph, results);
    cout << "x1 covariance:\n" << marginals.marginalCovariance(Symbol('x', 1)) << endl;
    cout << "x2 covariance:\n" << marginals.marginalCovariance(Symbol('x', 2)) << endl;
    cout << "x3 covariance:\n" << marginals.marginalCovariance(Symbol('x', 3)) << endl;
    cout << "x4 covariance:\n" << marginals.marginalCovariance(Symbol('x', 4)) << endl;
    cout << "x5 covariance:\n" << marginals.marginalCovariance(Symbol('x', 5)) << endl;

    return 0;
}

过程解析：
第一步： 构建因子图模型

 NonlinearFactorGraph graph;

第二步：初始化顶点值

Values initials;
initials.insert(Symbol('x', 1), Pose2(0.2, -0.3, 0.2));
initials.insert(Symbol('x', 2), Pose2(5.1, 0.3, -0.1));
initials.insert(Symbol('x', 3), Pose2(9.9, -0.1, -M_PI_2 - 0.2));
initials.insert(Symbol('x', 4), Pose2(10.2, -5.0, -M_PI + 0.1));
initials.insert(Symbol('x', 5), Pose2(5.1, -5.1, M_PI_2 - 0.1));

第三步：固定第一个顶点，添加一个系统先验，一元因子

noiseModel::Diagonal::shared_ptr priorModel = noiseModel::Diagonal::Sigmas(Vector3(1.0, 1.0, 0.1));
graph.add(PriorFactor<Pose2>(Symbol('x', 1), Pose2(0, 0, 0), priorModel));

第四步：添加位姿间约束，二元因子

noiseModel::Diagonal::shared_ptr odomModel = noiseModel::Diagonal::Sigmas(Vector3(0.5, 0.5, 0.1));
graph.add(BetweenFactor<Pose2>(Symbol('x', 1), Symbol('x', 2), Pose2(5, 0, 0), odomModel));
graph.add(BetweenFactor<Pose2>(Symbol('x', 2), Symbol('x', 3), Pose2(5, 0, -M_PI_2), odomModel));
graph.add(BetweenFactor<Pose2>(Symbol('x', 3), Symbol('x', 4), Pose2(5, 0, -M_PI_2), odomModel));
graph.add(BetweenFactor<Pose2>(Symbol('x', 4), Symbol('x', 5), Pose2(5, 0, -M_PI_2), odomModel));

第五步：添加回环间约束，二元因子

noiseModel::Diagonal::shared_ptr loopModel = noiseModel::Diagonal::Sigmas(Vector3(0.5, 0.5, 0.1));
graph.add(BetweenFactor<Pose2>(Symbol('x', 5), Symbol('x', 2), Pose2(5, 0, -M_PI_2), loopModel));
  

第六步：问题求解，这里用的是高斯牛顿法

 GaussNewtonParams parameters;
 parameters.setVerbosity("ERROR");
 parameters.setMaxIterations(20);
 parameters.setLinearSolverType("MULTIFRONTAL_QR");
 GaussNewtonOptimizer optimizer(graph, initials, parameters);//因子图  初始值  参数对象
 Values results = optimizer.optimize();
 results.print("Final Result:\n");

第七步：边缘化，计算每个变量的协方差矩阵

Marginals marginals(graph, results);

运行结果：

Factor Graph:
size: 6

Factor 0: PriorFactor on x1
  prior mean: (0, 0, 0)
  noise model: diagonal sigmas[1; 1; 0.1];

Factor 1: BetweenFactor(x1,x2)
  measured: (5, 0, 0)
  noise model: diagonal sigmas[0.5; 0.5; 0.1];

Factor 2: BetweenFactor(x2,x3)
  measured: (5, 0, -1.57079633)
  noise model: diagonal sigmas[0.5; 0.5; 0.1];

Factor 3: BetweenFactor(x3,x4)
  measured: (5, 0, -1.57079633)
  noise model: diagonal sigmas[0.5; 0.5; 0.1];

Factor 4: BetweenFactor(x4,x5)
  measured: (5, 0, -1.57079633)
  noise model: diagonal sigmas[0.5; 0.5; 0.1];

Factor 5: BetweenFactor(x5,x2)
  measured: (5, 0, -1.57079633)
  noise model: diagonal sigmas[0.5; 0.5; 0.1];


Initial Values:
Values with 5 values:
Value x1: (N5gtsam5Pose2E) (0.2, -0.3, 0.2)

Value x2: (N5gtsam5Pose2E) (5.1, 0.3, -0.1)

Value x3: (N5gtsam5Pose2E) (9.9, -0.1, -1.77079633)

Value x4: (N5gtsam5Pose2E) (10.2, -5, -3.04159265)

Value x5: (N5gtsam5Pose2E) (5.1, -5.1, 1.47079633)

Initial error: 18.510326
newError: 0.122934358
errorThreshold: 0.122934358 > 0
absoluteDecrease: 18.3873916591 >= 1e-05
relativeDecrease: 0.993358606565 >= 1e-05
newError: 8.85829965247e-06
errorThreshold: 8.85829965247e-06 > 0
absoluteDecrease: 0.12292549938 >= 1e-05
relativeDecrease: 0.999927942848 >= 1e-05
newError: 3.68234845905e-15
errorThreshold: 3.68234845905e-15 > 0
absoluteDecrease: 8.85829964879e-06 < 1e-05
relativeDecrease: 0.999999999584 >= 1e-05
converged
errorThreshold: 3.68234845905e-15 <? 0
absoluteDecrease: 8.85829964879e-06 <? 1e-05
relativeDecrease: 0.999999999584 <? 1e-05
iterations: 3 >? 100
Final Result:
Values with 5 values:
Value x1: (N5gtsam5Pose2E) (-3.17592454561e-18, 5.21439530413e-19, 2.17083859205e-20)

Value x2: (N5gtsam5Pose2E) (5, 7.60341342619e-19, 1.73447953203e-20)

Value x3: (N5gtsam5Pose2E) (10.0000000015, -4.40576430129e-09, -1.5707963267)

Value x4: (N5gtsam5Pose2E) (10.0000000114, -5.00000003139, 3.14159265352)

Value x5: (N5gtsam5Pose2E) (4.99999999784, -5.00000000264, 1.57079632663)

x1 covariance:
                 1  1.09613818193e-18 -3.52006030097e-17
 1.09613818193e-18                  1  1.42108547152e-16
-3.52006030097e-17  1.42108547152e-16               0.01
x2 covariance:
              1.25 -2.18298661793e-16  -8.8071537939e-17
-2.18298661793e-16                1.5               0.05
 -8.8071537939e-17               0.05               0.02
x3 covariance:
     2.70000000047 -8.21534004474e-10    -0.155000000029
-8.21533972918e-10      1.45000000006  -0.00499999990562
   -0.155000000029  -0.00499999990562    0.0264999999985
x4 covariance:
   2.1125000074  0.800000006448 -0.120000000784
 0.800000006448   2.80000000387 -0.170000000296
-0.120000000784 -0.170000000296 0.0279999999952
x5 covariance:
  1.69999999991 -0.224999999954 0.0449999999659
-0.224999999954   2.06250000049 -0.127500000037
0.0449999999659 -0.127500000037 0.0264999999968

cmakeLists.txt文件：

project(gtsam_test)
cmake_minimum_required(VERSION 2.8)
add_compile_options(-std=c++11)
find_package(Boost COMPONENTS thread filesystem date_time system REQUIRED)
FIND_PACKAGE(GTSAM REQUIRED)

INCLUDE_DIRECTORIES(${Boost_INCLUDE_DIR})
INCLUDE_DIRECTORIES(${GTSAM_INCLUDE_DIR})
INCLUDE_DIRECTORIES("/usr/include/eigen3")
add_executable(test test.cpp)
# 链接库 
target_link_libraries(test ${Boost_LIBRARIES} -lgtsam -ltbb)
install(TARGETS test RUNTIME DESTINATION bin)

参考：
1.官方教程：https://gtsam.org/tutorials/intro.html#listing_OdometryOptimize

至于ISAM2 *isam的应用，还没太明白，后面补充吧。