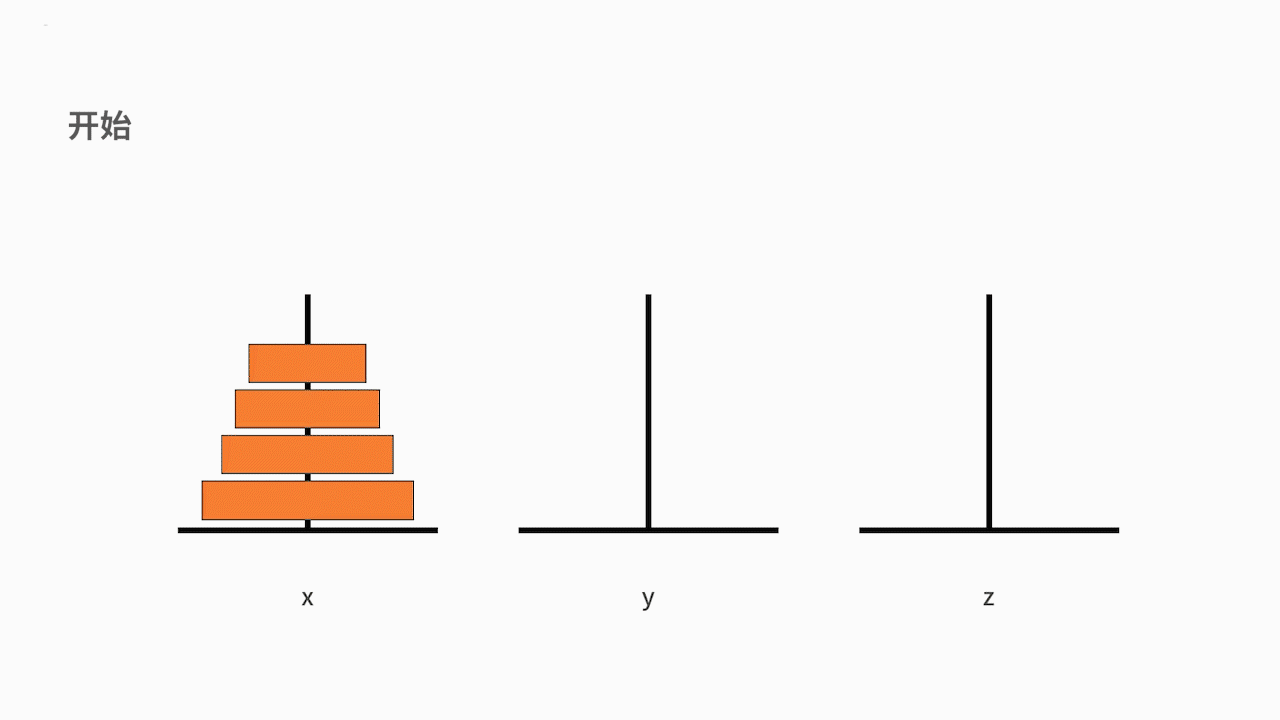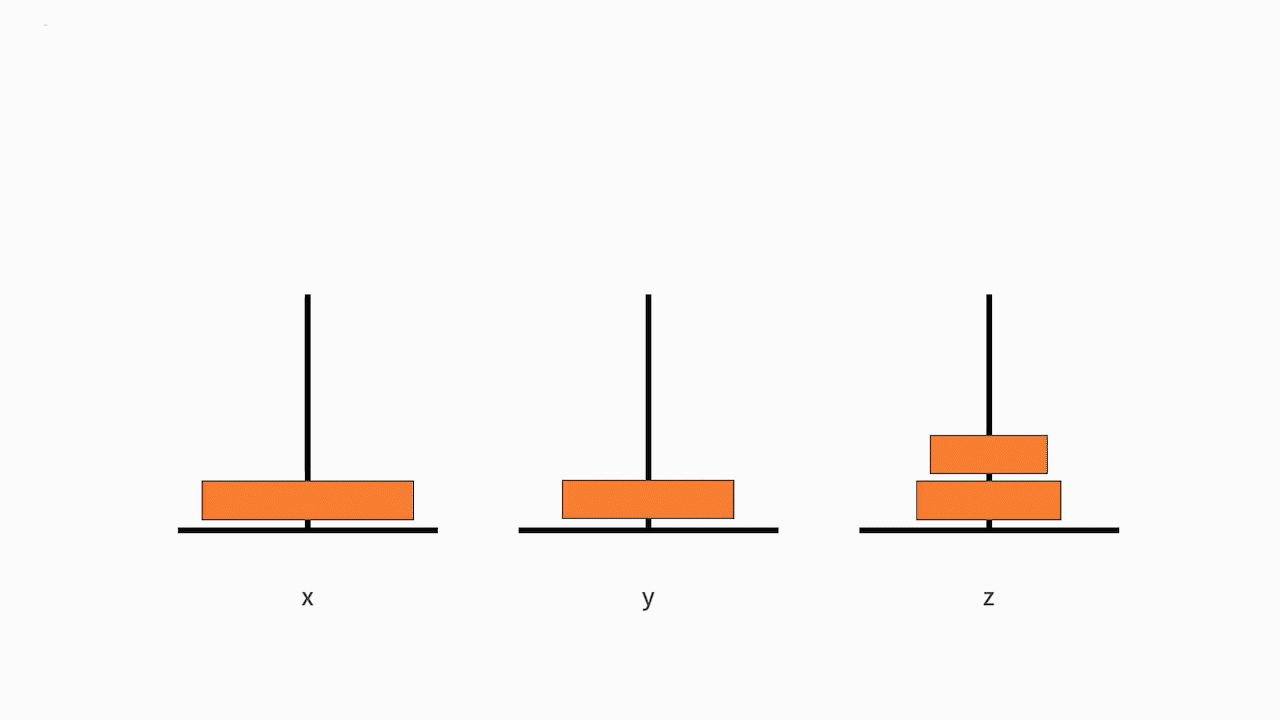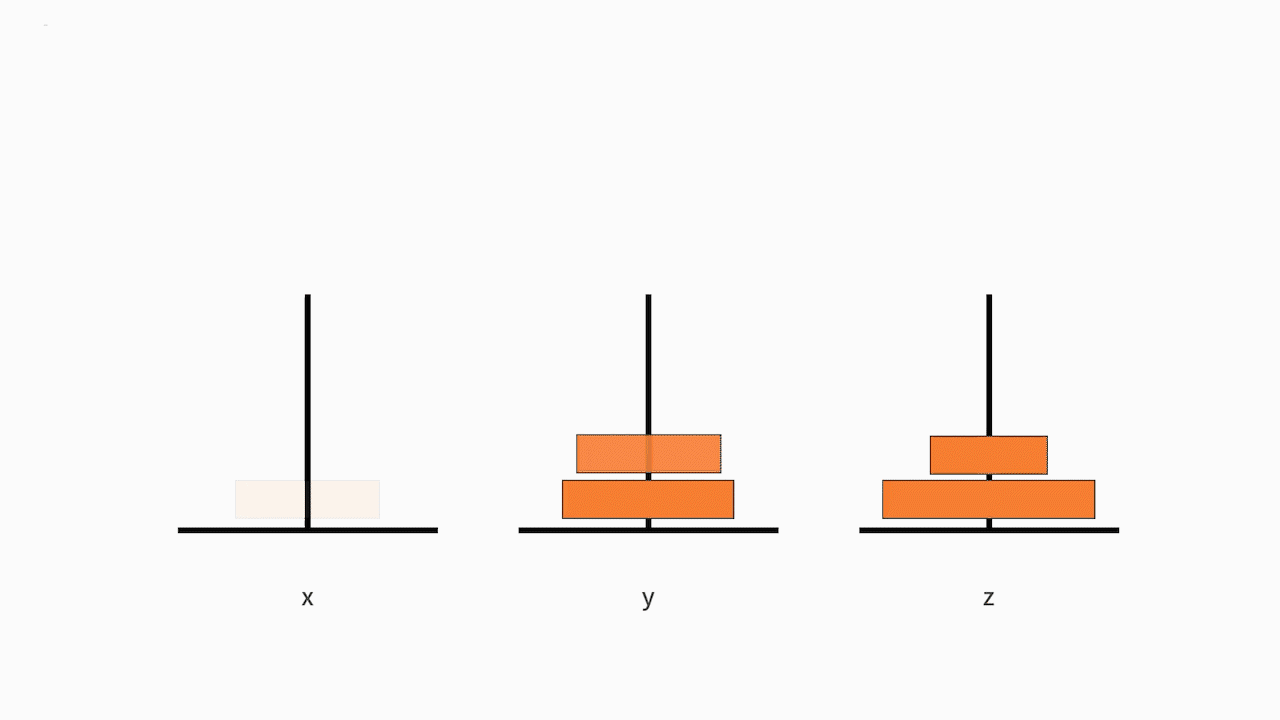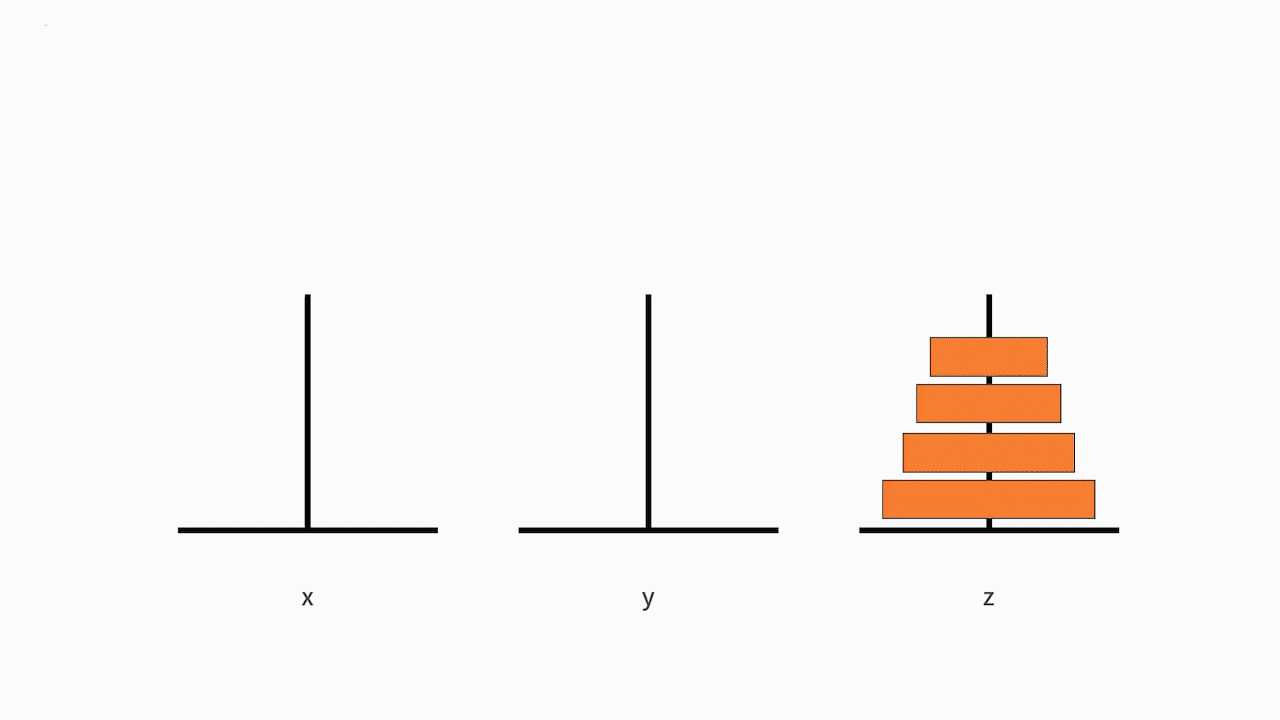递归：如何利用递归求解汉诺塔问题？回溯：组合总和、N皇后

目录

递归

递归的算法思想

汉诺塔问题

总结

91. 解码方法

回溯

解决问题套路

39. 组合总和

52 N皇后

总结

---

递归

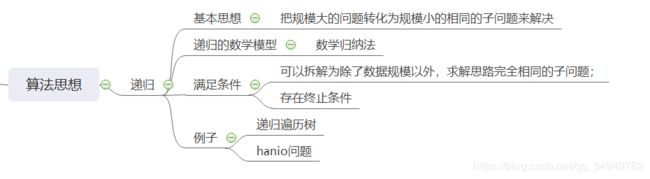
递归的基本思想就是把规模大的问题转化为规模小的相同的子问题来解决。 在函数实现时，因为大问题和小问题是一样的问题，因此大问题的解决方法和小问题的解决方法也是同一个方法。这就产生了函数调用它自身的情况，这也正是递归的定义所在。

递归的算法思想

递归的数学模型其实就是数学归纳法。一个常见的题目是：证明当 n 等于任意一个自然数时某命题成立。

当采用数学归纳法时，证明分为以下 2 个步骤：

• 证明当 n = 1 时命题成立；

• 假设 n = m 时命题成立，那么尝试推导出在 n = m + 1 时命题也成立。

所以当一个问题同时满足以下 2 个条件时，就可以使用递归的方法求解：

• 可以拆解为除了数据规模以外，求解思路完全相同的子问题；

• 存在终止条件。

例如中序遍历。采用递归实现中序遍历时，程序执行的逻辑架构如下图所示：

 

其中，每个蓝色的括号都是一次递归调用，即问题转化，打印是终止条件。

我们总结一下，写出递归代码的关键在于，写出递推公式和找出终止条件。也就是说我们需要：首先找到将大问题分解成小问题的规律，并基于此写出递推公式；然后找出终止条件，就是当找到最简单的问题时，如何写出答案；最终将递推公式和终止条件翻译成实际代码。

汉诺塔问题

如下图所示，从左到右有 x、y、z 三根柱子，其中 x 柱子上面有从小叠到大的 n 个圆盘。现要求将 x 柱子上的圆盘移到 z 柱子上去。要求是，每次只能移动一个盘子，且大盘子不能被放在小盘子上面。求移动的步骤。

我们的原问题是，把从小到大的 n 个盘子，从 x 移动到 z。

我们可以将这个大问题拆解为以下 3 个小问题：

• 把从小到大的 n-1 个盘子，从 x 移动到 y；

• 接着把最大的一个盘子，从 x 移动到 z；

• 再把从小到大的 n-1 个盘子，从 y 移动到 z。

首先，我们来判断它是否满足递归的第一个条件。 其中，第 1 和第 3 个问题就是汉诺塔问题。这样我们就完成了一次把大问题缩小为完全一样的小规模问题。我们已经定义好了递归体，也就是满足来递归的第一个条件。如下图所示：

接下来我们来看判断它是否满足终止条件。随着递归体不断缩小范围，汉诺塔问题由原来“移动从小到大的 n 个盘子”，缩小为“移动从小到大的 n-1 个盘子”，直到缩小为“移动从小到大的 1 个盘子”。移动从小到大的 1 个盘子，就是移动最小的那个盘子。根据规则可以发现，最小的盘子是可以自由移动的。因此，递归的第二个条件，终止条件，也是满足的。

代码：

package cn.ren.demo;

public class Hanio {
	public static void hanio(int n, String x, String y, String z) {
		if (n == 1) { // 终止条件
			System.out.println(x + " -> " + z);
			return;
		} else {
			hanio(n - 1, x, z, y); // 将 n-1 个移动到y
			System.out.println(x + " -> " + z); // 将最大一个移动到z
			hanio(n - 1, y, x, z); // 将n-1个移动到z
		}
	}

	public static void main(String[] args) {
		String x = "x";
		String y = "y";
		String z = "z";
		hanio(3, x, y, z);
	}
}

 

抛开用于处理输入异常的代码部分不谈，它的代码包含了 2 个部分：

• 终止条件，即如何处理小规模的问题，实现的代码量一定是很少的；

• 递归体，即大问题向小问题分解的过程，实现的代码量也不会太多。

因此，一个复杂问题的递归实现，通常代码量都不会很多。

总结

时间复杂度分析：

迭代法：

公式法：

 

91. 解码方法

class Solution {
    public int numDecodings(String s) {
    	if(s.startsWith("0")) {
    		return 0 ;
    	}
    	char [] chars = s.toCharArray() ;
    	return decode(chars, chars.length - 1) ;
    }
    public int decode(char [] chars, int index) {
    	if(index <= 0) {
    		return 1 ;
    	}
    	
    	int count = 0 ; 
    	char curr = chars[index] ;
    	char prev = chars[index - 1] ;
    	
    	if(curr > '0') {
    		count = decode(chars, index -1) ; // 最后一个当一个元素
    	}
    	if(prev == '1' || (prev == '2' && curr <= '6')) {
    		count += decode(chars, index - 2) ; // 大于9的情况，最后两个当一个元素
    	}
    	return count ;
    }
}

回溯

解决问题套路

39. 组合总和

class Solution {
          public static List> combinationSum(int[] candidates, int target) {
    	List> results = new ArrayList>() ;
    	List solution = new ArrayList() ;
    	backtracking(candidates, target, 0, solution, results) ;
    	return results ;
    	
    }
    public static void backtracking(int[] candidates, int target, int start, List solution , List> results) {
    	if(target < 0) {
    		return;
    	}
    	if(target == 0) { 
    		results.add(new ArrayList(solution)) ;  // 避免之后solution变换影响存放在results的结果，new在栈空间里面建立指针
    		return ;
    	}
    	for(int i = start; i < candidates.length; i ++) {
    		solution.add(candidates[i]) ;
    		backtracking(candidates, target - candidates[i], i, solution, results) ;
    		solution.remove(solution.lastIndexOf(candidates[i])) ;
    	}
    }
}

52 N皇后

之后更

总结