【机器学习系列】之支持向量回归SVR

作者：張張張張
github地址：https://github.com/zhanghekai
【转载请注明出处，谢谢！】

【机器学习系列】之SVM硬间隔和软间隔
【机器学习系列】之SVM核函数和SMO算法
【机器学习系列】之支持向量回归SVR
【机器学习系列】之sklearn实现SVM代码

一、SVM回归模型概述

对于SVM回归模型：给定样本$D=\{(x_1,y_1),(x_2,y_2),\cdots ,(x_m,y_m)\},y\in R$(由于是回归模型，$y$没有类别)，我们的目标是让训练集中的每个点$(x_i,y_i)$尽量拟合到一个线性模型$y_i=w\cdot \varphi (x_i)+b$。

对于一般的回归模型： 通常采用均方差作为损失函数。传统回归模型通常直接基于“模型输出”与“真实输出”之间的差别来计算损失，当切仅当二者完全相同时，损失才为$0$。

对于SVM回归模型： “支持向量回归（Support Vector Regression）”需要定义一个常量$ϵ>0$,$ϵ$为能容忍“模型输出”与“真实输出”之间最多有$ϵ$的偏差。

• 如果$|y_i-w\cdot \varphi (x_i)-b|\le ϵ$，则完全没有损失；
• 如果$|y_i-w\cdot \varphi (x_i)-b|\ge ϵ$，则对应的损失为$|y_i-w\cdot \varphi (x_i)-b|-ϵ$

即： 仅当$f(x)=w\cdot \varphi (x_i)-b$与$y$之间的差别绝对值大于$ϵ$时才计算损失。

如下图所示，这相当于以$f(x)$为中心，构建了一个宽度为$2ϵ$的间隔带，若训练样本落入此间隔带，则认为是被预测正确的。

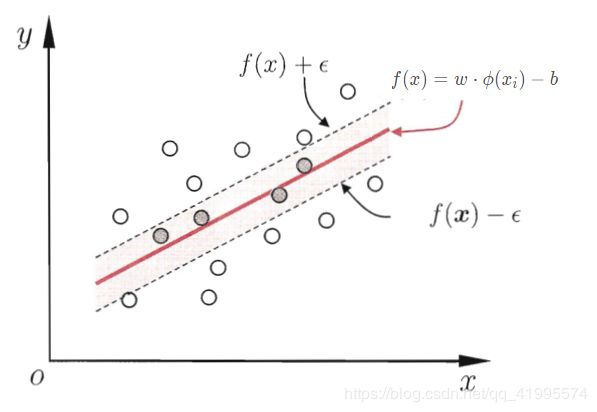
综上所述，SVM回归模型的损失函数度量为：
$$err(x_i,y_i)=\{\begin{array}{l}0,|y_i-w\cdot \varphi (x_i)-b|\le ϵ\\ |y_i-w\cdot \varphi (x_i)-b|-ϵ,|y_i-w\cdot \varphi (x_i)-b|>ϵ\end{array}$$

二、SVM回归模型目标函数

定义SVM回归模型目标函数为：
$$\begin{gathered} \underset{w,b}{min}\frac{1}{2}||w|{|}^2 \\ s.t.|y_i-w\cdot \varphi (x_i)-b|\le ϵ(i=1,2,\cdots ,m) \end{gathered}$$

回归模型也可以对每个样本加入松弛变量，但由于这里$s.t.$处用的是绝对值，实际上是两个不等式，即两边都需要松弛变量，定义松弛变量为$\check{\xi }、\hat{\xi }$，加入松弛变量后的SVM回归模型的损失函数为：
$$\begin{gathered} \underset{w,b,{\check{\xi }}_i,{\hat{\xi }}_i}{min}\frac{1}{2}||w|{|}^2+C\sum _{i=1}^m({\check{\xi }}_i+{\hat{\xi }}_i) \\ s.t.-ϵ-{\check{\xi }}_i\le y_i-w\cdot \varphi (x_i)-b\le ϵ+{\hat{\xi }}_i \\ {\check{\xi }}_i\ge 0,{\hat{\xi }}_i\ge 0(i=1,2,\cdots ,m) \end{gathered}$$

间隔带两侧的松弛程度可有所不同。

同SVM分类模型相似，可以用拉格朗日函数将目标优化哈数变成无约束的形式：

• 带求目标$f(x)=\underset{w,b,{\check{\xi }}_i,{\hat{\xi }}_i}{min}\frac{1}{2}||w|{|}^2+C{\sum }_{i=1}^m({\check{\xi }}_i+{\hat{\xi }}_i)$
• 不等式约束：
  • $h_1(x)=y_i-w\cdot \varphi (x_i)-b-ϵ-{\hat{\xi }}_i\le 0$
  • $h_2(x)=w\cdot \varphi (x_i)+b-y_i-ϵ-{\check{\xi }}_i\le 0$
  • $g_1(x)=-{\check{\xi }}_i\le 0$
  • $g_2(x)=-{\hat{\xi }}_i\le 0$
• 拉格朗日乘子：
  • ${\hat{\alpha }}_i=({\hat{\alpha }}_1,{\hat{\alpha }}_2,\cdots ,{\hat{\alpha }}_m)$
  • ${\check{\alpha }}_i=({\check{\alpha }}_1,{\check{\alpha }}_2,\cdots ,{\check{\alpha }}_m)$
  • ${\hat{\mu }}_i=({\hat{\mu }}_1,{\hat{\mu }}_2,\cdots ,{\hat{\mu }}_m)$
  • ${\check{\mu }}_i=({\check{\mu }}_1,{\check{\mu }}_2,\cdots ,{\check{\mu }}_m)$
• 拉格朗日函数：
  $$\begin{gathered} L(w,b,{\check{\xi }}_i,{\hat{\xi }}_i,{\check{\alpha }}_i,{\hat{\alpha }}_i,{\check{\mu }}_i,{\hat{\mu }}_i)=f(x)+{\hat{\alpha }}_i{h}_1(x)+{\check{\alpha }}_i{h}_2(x)+{\check{\mu }}_i{g}_1(x)+{\hat{\mu }}_i{g}_2(x) \\ =\frac{1}{2}||w|{|}^2+C\sum _{i=1}^m({\check{\xi }}_i+{\hat{\xi }}_i)+\sum _{i=1}^m{\hat{\alpha }}_i(y_i-w\cdot \varphi (x_i)-b-ϵ-{\hat{\xi }}_i) \\ +\sum _{i=1}^m{\check{\alpha }}_i(x\cdot \varphi (x_i)+b-y_i-ϵ-\check{\xi })-\sum _{i=1}^m{\check{\mu }}_i{\check{\xi }}_i-\sum _{i=1}^m{\hat{\mu }}_i{\hat{\xi }}_i \end{gathered}$$

SVM回归模型原始形式：
$$\underset{w,b,{\check{\xi }}_i,{\hat{\xi }}_i}{min}\underset{{\hat{\alpha }}_i\ge 0,{\check{\alpha }}_i\ge 0,{\hat{\mu }}_i\ge 0,{\check{\mu }}_i\ge 0}{max}L(w,b,{\check{\xi }}_i,{\hat{\xi }}_i,{\check{\alpha }}_i,{\hat{\alpha }}_i,{\check{\mu }}_i,{\hat{\mu }}_i)$$

和SVM分类模型一样，这个优目标也满足KKT条件，可以通过拉格朗日对偶将优化问题转化为等价的对偶问题来求解：
$$\underset{{\hat{\alpha }}_i\ge 0,{\check{\alpha }}_i\ge 0,{\hat{\mu }}_i\ge 0,{\check{\mu }}_i\ge 0}{max}\underset{w,b,{\check{\xi }}_i,{\hat{\xi }}_i}{min}L(w,b,{\check{\xi }}_i,{\hat{\xi }}_i,{\check{\alpha }}_i,{\hat{\alpha }}_i,{\check{\mu }}_i,{\hat{\mu }}_i)$$
可以先求优化函数对于$w,b,{\check{\xi }}_i,{\hat{\xi }}_i$的极小值，接着再求拉格朗日乘子${\hat{\alpha }}_i,{\check{\alpha }}_i,{\hat{\mu }}_i,{\check{\mu }}_i$的极大值。

三、SVM回归模型目标函数求解

首先来求优化函数对于$w,b,{\check{\xi }}_i,{\hat{\xi }}_i$的极小值，这个可以通过对$L$求偏导数求得：
$$\begin{gathered} \frac{\partial L}{\partial w}=0⟹w=\sum _{i=1}^m({\hat{\alpha }}_i-{\check{\alpha }}_i)\varphi (x_i) \\ \frac{\partial L}{\partial b}=0⟹\sum _{i=1}^m({\hat{\alpha }}_i-{\check{\alpha }}_i)=0 \\ \frac{\partial L}{\partial {\check{\xi }}_i}=0⟹C={\check{\alpha }}_i+{\check{\mu }}_i \\ \frac{\partial L}{\partial {\hat{\xi }}_i}=0⟹C={\hat{\alpha }}_i+{\hat{\mu }}_i \end{gathered}$$

将上述4个式子带入$L(w,b,{\check{\xi }}_i,{\hat{\xi }}_i,{\check{\alpha }}_i,{\hat{\alpha }}_i,{\check{\mu }}_i,{\hat{\mu }}_i)$，消去$w,b,{\check{\xi }}_i,{\hat{\xi }}_i$。
$$\begin{gathered} \underset{{\check{\alpha }}_i,{\hat{\alpha }}_i}{max}\sum _{i=1}^m(y_i({\hat{\alpha }}_i-{\check{\alpha }}_i)-ϵ({\hat{\alpha }}_i+{\check{\alpha }}_i))-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m({\hat{\alpha }}_i-{\check{\alpha }}_i)({\hat{\alpha }}_j-{\check{\alpha }}_j){\kappa }_{ij} \\ s.t.\sum _{i=1}^m({\hat{\alpha }}_i-{\check{\alpha }}_i)=0 \\ 0<\check{{\alpha }_i}<C(i=1,2,\cdots ,m) \\ 0<{\hat{\alpha }}_i<C(i=1,2,\cdots ,m) \end{gathered}$$

对目标函数取负号，得到求极小值的目标函数如下：
$$\begin{gathered} \underset{{\hat{\alpha }}_i,{\check{\alpha }}_i}{min}\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m({\hat{\alpha }}_i-{\check{\alpha }}_i)({\hat{\alpha }}_j-{\check{\alpha }}_j){\kappa }_{ij}-\sum _{i=1}^m(y_i({\hat{\alpha }}_i-{\check{\alpha }}_i)-ϵ({\hat{\alpha }}_i+{\check{\alpha }}_i)) \\ s.t.\sum _{i=1}^m({\hat{\alpha }}_i-{\check{\alpha }}_i)=0 \\ 0<\check{{\alpha }_i}<C(i=1,2,\cdots ,m) \\ 0<{\hat{\alpha }}_i<C(i=1,2,\cdots ,m) \end{gathered}$$

对于这个目标函数，依然可以用SMO算法来求出对应的$\check{{\alpha }_i},\widehat{{\alpha }_i}$，进而求出回归模型系数$w,b$。

四、SVM回归模型系数的系数的稀疏性

上述过程需满足KKT条件，即要求：
$$\{\begin{array}{l}{\hat{\alpha }}_i(y_i-w\cdot \varphi (x_i)-b-ϵ-{\hat{\xi }}_i)=0\\ {\check{\alpha }}_i(x\cdot \varphi (x_i)+b-y_i-ϵ-{\check{\xi }}_i)=0\\ {\check{\alpha }}_i{\hat{\alpha }}_i=0,{\check{\xi }}_i{\hat{\xi }}_i=0\\ (C-{\check{\alpha }}_i){\check{\xi }}_i=0,(C-{\hat{\alpha }}_i){\hat{\xi }}_i=0\end{array}$$

由KKT条件知：

• 当且仅当$y_i-w\cdot \varphi (x_i)-b-ϵ-{\hat{\xi }}_i=0$时，${\hat{\alpha }}_i$能取非零值；
• 当且仅当$x\cdot \varphi (x_i)+b-y_i-ϵ-{\check{\xi }}_i=0$时，${\check{\alpha }}_i$能取非零值；
• 总结： 仅当样本$(x_i,y_i)$不落入$ϵ-$间隔带中，相应的${\check{\alpha }}_i$和${\hat{\alpha }}_i$才能取非零值。
• 约束$y_i-w\cdot \varphi (x_i)-b-ϵ-{\hat{\xi }}_i=0$和$x\cdot \varphi (x_i)+b-y_i-ϵ-{\check{\xi }}_i=0$不能同时成立，因此${\check{\alpha }}_i$和${\hat{\alpha }}_i$中至少有一个为$0$。
• 落在$ϵ-$间隔带中的样本都满足${\check{\alpha }}_i=0$且${\hat{\alpha }}_i=0$。

最终SVM线性回归的解形式如下：
$$f(x)=\sum _{i=1}^m({\hat{\alpha }}_i-{\check{\alpha }}_i)\kappa (x,x_i)+b$$
其中$\kappa (x_i,x_j)=\varphi (x_i{)}^T\varphi (x_j)$为核函数。

能使$f(x)$中的$({\hat{\alpha }}_i-{\check{\alpha }}_i)$不等于$0$的样本即为SVR的支持向量，它们必落在$ϵ-$间隔带之外。 显然，SVR的支持向量仅是训练样本的一部分。

由KKT条件可以看出，对每个样本$(x_i,y_i)$都有： $(C-{\check{\alpha }}_i){\check{\xi }}_i=0$且${\check{\alpha }}_i(x\cdot \varphi (x_i)+b-y_i-ϵ-{\check{\xi }}_i)=0$。于是，在得到${\check{\alpha }}_i$后，若$0<{\check{\alpha }}_i<C$，必有$\check{{\xi }_i}=0$，则$x\cdot \varphi (x_i)+b-y_i-ϵ=0$，进而有：
$$b=y_i+ϵ-\sum _{j=1}^m({\hat{\alpha }}_j-{\check{\alpha }}_j)x_j^T{x}_i$$
因此，通过SMO算法得到${\check{\alpha }}_i$后，可任意选取满足$0<{\check{\alpha }}_i<C$的样本通过上式求得$b$。实践中常采用一种更鲁棒的办法：选取多个（或所有）满足条件$0<{\check{\alpha }}_i<C$的样本求解b后取平均值。

---

【参考文献】

• 刘建平 博客园：https://www.cnblogs.com/pinard/
• 周志华 《机器学习》