基本数据结构-------链表List与链表节点ListNode
来源: http://www.cppblog.com/cxiaojia/archive/2012/07/31/185760.html
- 线性表?分类(优缺点,查找、删除、插入的复杂度)?例子?
- 链表和线性表的关系?
- 链表的分类?是根据什么划分的?
线性表
线性表中数据元素之间的关系是一对一的关系,即除了第一个和最后一个数据元素之外,其它数据元素都是首尾相接的。
线性表分类:顺序存储结构、链式存储结构
例子:数组
顺序存储结构:两个相邻的元素在内存中也是相邻的。通过首地址和偏移量就可以直接访问到某元素,关于查找的适配算法很多,最快可以达到O(logn)。缺点是插入和删除的时间复杂度最坏能达到O(n),要开辟稍大点的内存,造成内存浪费。
链式存储结构:相邻的元素在内存中可能不是相邻的,每一个元素都有一个指针域,指针域一般是存储着到下一个元素的指针。优点是插入和删除的时间复杂度为O(1),不会浪费太多内存,添加元素的时候才会申请内存,删除元素会释放内存,。缺点是访问的时间复杂度最坏为O(n),关于查找的算法很少,一般只能遍历,这样时间复杂度也是线性(O(n))的了,频繁的申请和释放内存也会消耗时间。
链表
链表就是链式存储的线性表。
根据指针域的不同,链表分为单向链表、双向链表、循环链表等等。
单向链表
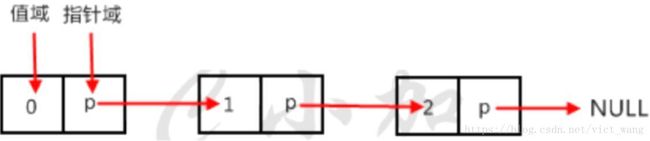
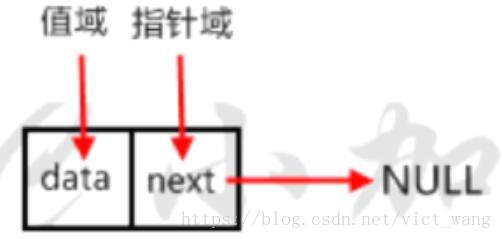
每个元素包含两个域,值域和指针域,我们把这样的元素称之为节点。每个节点的指针域内有一个指针,指向下一个节点,而最后一个节点则指向一个空值(一个方向遍历)。如图就是一个单向链表。
代码编写:
1.写节点类,则链表中的每一个结点可表示出来(实例化)
template
class slistNode
{
public:
slistNode(){next=NULL;}//初始化
T data;//值
slistNode* next;//指向下一个节点的指针
}; 2.写单链表类的声明,包括属性和方法。
template
class myslist
{
private:
unsigned int listlength;
slistNode* node;//临时节点
slistNode* lastnode;//尾结点
slistNode* headnode;//头节点
public:
myslist();//初始化
unsigned int length();//链表元素的个数
void add(T x);//表尾添加元素
void traversal();//遍历整个链表并打印
bool isEmpty();//判断链表是否为空
slistNode* find(T x);//查找第一个值为x的节点,返回节点的地址,找不到返回NULL
void Delete(T x);//删除第一个值为x的节点
void insert(T x,slistNode* p);//在p节点后插入值为x的节点
void insertHead(T x);//在链表的头部插入节点
};
3.写构造函数,初始化链表类的属性。
template
myslist::myslist()
{
node=NULL;
lastnode=NULL;
headnode=NULL;
listlength=0;
} 4.方法的实现
template
void myslist::add(T x)
{
node=new slistNode();//申请一个新的节点
node->data=x;//新节点赋值为x
if(lastnode==NULL)//如果没有尾节点则链表为空,node既为头结点,又是尾节点
{
headnode=node;
lastnode=node;
}
else//如果链表非空
{
lastnode->next=node;//node既为尾节点的下一个节点
lastnode=node;//node变成了尾节点,把尾节点赋值为node
}
++listlength;//元素个数+1
}
template
void myslist::traversal()
{
node=headnode;//用临时节点指向头结点
while(node!=NULL)//遍历链表并输出
{
cout<data<next;
}
cout<
bool myslist::isEmpty()
{
return listlength==0;
}
template
slistNode* myslist::find(T x)
{
node=headnode;//用临时节点指向头结点
while(node!=NULL&&node->data!=x)//遍历链表,遇到值相同的节点跳出
{
node=node->next;
}
return node;//返回找到的节点的地址,如果没有找到则返回NULL
}
5.删除插入方法的解析,删除第一个值为x的节点,如图
template
void myslist::Delete(T x)
{
slistNode* temp=headnode;//申请一个临时节点指向头节点
if(temp==NULL) return;//如果头节点为空,则该链表无元素,直接返回
if(temp->data==x)//如果头节点的值为要删除的值,则删除投节点
{
headnode=temp->next;//把头节点指向头节点的下一个节点
if(temp->next==NULL) lastnode=NULL;//如果链表中只有一个节点,删除之后就没有节点了,把尾节点置为空
delete(temp);//删除头节点
return;
}
while(temp->next!=NULL&&temp->next->data!=x)//遍历链表找到第一个值与x相等的节点,temp表示这个节点的上一个节点
{
temp=temp->next;
}
if(temp->next==NULL) return;//如果没有找到则返回
if(temp->next==lastnode)//如果找到的时候尾节点
{
lastnode=temp;//把尾节点指向他的上一个节点
delete(temp->next);//删除尾节点
temp->next=NULL;
}
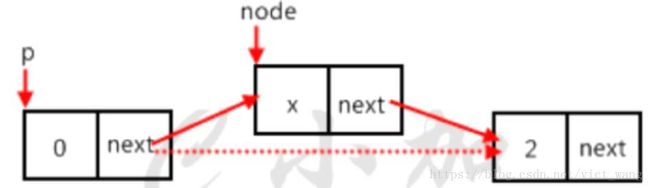
else//如果不是尾节点,如图4
{
node=temp->next;//用临时节点node指向要删除的节点
temp->next=node->next;//要删除的节点的上一个节点指向要删除节点的下一个节点
delete(node);//删除节点
node=NULL;
}
} 6.实现insert()和insertHead()函数,在p节点后插入值为x的节点。如图
template
void myslist::insert(T x,slistNode* p)
{
if(p==NULL) return;
node=new slistNode();//申请一个新的空间
node->data=x;//如图5
node->next=p->next;
p->next=node;
if(node->next==NULL)//如果node为尾节点
lastnode=node;
}
template
void myslist::insertHead(T x)
{
node=new slistNode();
node->data=x;
node->next=headnode;
headnode=node;
} 双向链表
双向链表的指针域有两个指针,每个数据结点分别指向直接后继和直接前驱。单向链表只能从表头开始向后遍历,而双向链表不但可以从前向后遍历,也可以从后向前遍历。除了双向遍历的优点,双向链表的删除的时间复杂度会降为O(1),因为直接通过目的指针就可以找到前驱节点,单向链表得从表头开始遍历寻找前驱节点。缺点是每个节点多了一个指针的空间开销。如图就是一个双向链表。
循环链表
循环链表就是让链表的最后一个节点指向第一个节点,这样就形成了一个圆环,可以循环遍历。单向循环链表可以单向循环遍历,双向循环链表的头节点的指针也要指向最后一个节点,这样的可以双向循环遍历。如图就是一个双向循环链表。
链表相关面试问题
- 如何判断一个单链表有环
- 如何判断一个环的入口点在哪里
- 如何知道环的长度
- 如何知道两个单链表(无环)是否相交
- 如果两个单链表(无环)相交,如何知道它们相交的第一个节点是什么
- 如何知道两个单链表(有环)是否相交
- 如果两个单链表(有环)相交,如何知道它们相交的第一个节点是什么
答案:https://blog.csdn.net/vividonly/article/details/6673758
#include
#define ListNodePosi(T) ListNode*//指针指向列表的结点:里面含有两个指针pred和succ
typedef int Rank;
template
class ListNode//列表节点模板类(以双向链表形式实现)
{
public:
T data;
ListNode* pred;//节点的前驱指针:指向前结点,而不是前节点的前驱或后驱指针
ListNode* succ;//节点的后继指针:指向后结点,而不是后节点的前驱或后驱指针
//构造函数
ListNode(){}
ListNode(T e, ListNodePosi(T) p = NULL, ListNodePosi(T) s = NULL) :data(e), pred(p), succ(s)
{
//默认构造器
}
//操作接口
ListNode* insertAsPred(T const& e);//结点前插入
ListNode* insertAsSucc(T const& e);//结点后插入
};
//note:链表节点类主要用于构建列表,所以直接用public
#include "listNode.h"
template
class List
{
private://私有的头哨兵和尾哨兵对外部不可见(eg:valid中从外部被等效的视为NULL),首节点尾结点是头哨兵之后的,尾哨兵之前的
int _size;
ListNode* header;//头哨兵:header->succ代表头结点
ListNode* trailer;//尾哨兵
protected:
void init();
int clear();
void copyNodes(ListNodePosi(T) p, int n);
void merge(ListNodePosi(T)&, int, List&, ListNodePosi(T), int);//有序列表区间合并
void merge(List& L) { merge(first(), size, L, L.first(), _size); }//全列表合并
void mergeSort(ListNodePosi(T)& p, int n);//对从p开始的n个节点归并排序
void selectionSort(ListNodePosi(T) p, int n);//...选择排序
void insertionSort(ListNodePosi(T) p, int n);//插入排序
public:
List() { init(); }
List(List const& L);
List(List const& L, Rank r, int n);
List(ListNodePosi(T) p, int n);
~List();//释放所有节点
..............
}