机器学习第八课——SVM(3)核函数与SMO算法
(1)简单回顾。
在继续学习之前,我要重新梳理一下上一节课的思路。未必都能够消化的前提下,这样做是必要的。
问题思路:求解最优间隔分类器的时候,我们如何求解出W,b,和 a ?
假设原问题的形式为:
![]()
对应的lagrange函数是:
![]()
我们通过相应的转换可以得到相应的dual问题形式:首先在假定a为定值的前提下,求解lagrange函数对w 和 b 的偏导数,并使得偏导数为0:
![]()
![]()
解得:
![]()
将上面的3条表达式代入到lagrange函数中,可得到只有 a 的lagrange函数表达式,此时,我们可以对lagrange函数求取关于a的导数,求得最大值时候的a*。知道a*的具体数值之后,我们也就可根据上一条式子求得w的数值,进而可求得b的数值。
刚刚的只是思路。具体过程如下:
将上面3条表达式代入lagrange函数后,lagrange函数可以表示为:
![]()
关于b的求解,我是存在疑问的。老师写出了表达式,如下:
![]()
我还没有想到到合理的解释。放在这里先,求高手指教。
(2)核函数。
为什么引进核函数?要回答这个问题,首先要回答的是:为什么要用高维数组来代替低维数组?
正和老师提出来的例子是相似的,我们想要估计特定面积的房子的价格,那么仅仅通过对一维数组x(面积)的分析进而拟合一个一次方程或二次方程来估计是比较难的,有时候甚至办不到。想到的方法就是:使用x, x², x³, 来作为可用数据来分析,那么就能够较为理想地拟合出估计方程。相对分类也是一样的,某些特征可能在低维的情况下无法分离出来,但是映射到高维就可以很好地分离出来(和LDA算法的原理相似),也就是特征数据低维线性不可分,高维线性可分(可分概率更大)。
引入核函数的缘由:避免高维数组的“维数灾难”。高维数组的计算复杂度高,有些时候甚至无法算出来。而通过核函数的概念,可以以复杂度较低的方式求解出高维数组内积的结果。我们看到,我们的SVM算法在计算过程中正是引入了内积的概念。核函数为解决SVM线性不可分问题转化为线性可分问题提供了合理方便的解决方法。
老师讲解的思路是先给出核函数的表达形式,进而再来找出相应的高维数组表达式。这一部分我的感想是:核函数是主要的,而高维数组的形式是次要的,甚至你可以不知道高维数组的具体表达形式,但是可以肯定的是,通过使用核函数,那么就已经将原来的低维数组转化为高维数组了,具体形式不用去理。
至于如何可以确定构造出来的核函数![]() 都存在一个高维数组 \fi 呢?老师那里给出了证明(Mercer定理),不再复述。
都存在一个高维数组 \fi 呢?老师那里给出了证明(Mercer定理),不再复述。
惊叹的是核函数应用的广泛性:核函数不仅仅用在SVM上,但凡在一个模型的算法中出现了![]() (只要能够构造出来),我们都可以使用
(只要能够构造出来),我们都可以使用![]() 去替换,替换之后也就是可在高维空间下来分析这个算法。
去替换,替换之后也就是可在高维空间下来分析这个算法。
我想记下课堂上学生们提的问题:(a)如何知道你通过核函数映射到高维空间中就一定可分呢?(b)如果不可分怎么办?(c)如果数据本来就是在任何维数下都是不可分的,那么如何解释这种现象?
(3)软间隔分类器
当映射到高维空间中就一定线性可分了吗?不一定,仅仅是线性可分的概率变大了而已。那么不可分怎么办呢?通过添加某一个因子的形式就可以实现(神经网络算法中也有这一种类型--添加动量因子),算是对基本算法形式的一种改变,优化原始算法以适应更广泛的情况。改变的形式如下:
![]()
该算法允许部分样本错分。具体不详细解释,老师讲的很清楚。对应的lagrange公式为:
![]()
式中的![]() 和
和![]() 都是拉格朗日乘子,和上一节课的推导过程类似,可以求得最后的推导结果是:
都是拉格朗日乘子,和上一节课的推导过程类似,可以求得最后的推导结果是:
![]()
因为![]() 又多了
又多了![]() 的限制条件,此时对应的KKT互补条件变为如下:
的限制条件,此时对应的KKT互补条件变为如下:
![]()
我想理解这个涵义是什么?之前很困惑,现找到一个合理的解释如下:
该式子表明在两条间隔线外的样本点前面的系数为0,离群样本点前面的系数为C,而支持向量(也就是在超平面两边的最大间隔线上)的样本点前面系数在(0,C)上。通过KKT条件可知,某些在最大间隔线上的样本点也不是支持向量(因为(14)(15)式中当中的不等号也有等号部分),相反也可能是离群点。
(4)SMO算法
首先需要引进的是坐标上升法:
让我们暂时不去考虑那些限制条件,来看看一个最值问题:
![]()
这里W是![]() 向量的函数。此方法可以与梯度下降法、牛顿方法联系在一起,都用于求解最值问题。该方法流程如下:
向量的函数。此方法可以与梯度下降法、牛顿方法联系在一起,都用于求解最值问题。该方法流程如下:
![]()
最里面语句的意思是固定除![]() 之外的所有
之外的所有![]() ,直接对W求取
,直接对W求取![]() 的导数,使得W处于极值(优化W)。在
的导数,使得W处于极值(优化W)。在![]() 的选择上,老师讲到我们既可以让 i 按照由1到m的顺序来优化W,也可以根据启发式法则(经验条件等)来选择
的选择上,老师讲到我们既可以让 i 按照由1到m的顺序来优化W,也可以根据启发式法则(经验条件等)来选择![]() 。和牛顿方法相比,该方法迭代次数较多,但是对于某些能够很快求得arg max的值的问题,该方法的效率很高。
。和牛顿方法相比,该方法迭代次数较多,但是对于某些能够很快求得arg max的值的问题,该方法的效率很高。
这是SMO算法的基础。下面让我们从坐标上升法的角度来考虑我们的问题:
可以看到,和没有限制条件的坐标上升法相比,我们的问题多了两个限制条件。当我们想固定除![]() 之外的所有
之外的所有![]() ,直接对W求取
,直接对W求取![]() 的导数时,限制条件说:你做不到,因为
的导数时,限制条件说:你做不到,因为![]() 被另外m-1个小伙伴约束着,m-1个元素固定,那么
被另外m-1个小伙伴约束着,m-1个元素固定,那么![]() 也无法改变。那么,John Platt 就告诉我们,那我们就试试一次改变两个a 吧,让其他m-2的元素保持不变,进而使用坐标上升法来优化问题。
也无法改变。那么,John Platt 就告诉我们,那我们就试试一次改变两个a 吧,让其他m-2的元素保持不变,进而使用坐标上升法来优化问题。
实际上,两个不同的a中,可以选择一个作为变量,另一个作为该变量的函数,相应的函数关系可以写成:
上式中,为方便表示,使用了a1、a2来表示这两个变化的ai;实际上任何ai均成立。
SMO算法可以描述如下:
循环中,在选取参数对时,可以使用一些启发式规则来选择使得W(a)变化最大的参数,详细的启发式规则老师没有说,参考John Platt的相关论文。
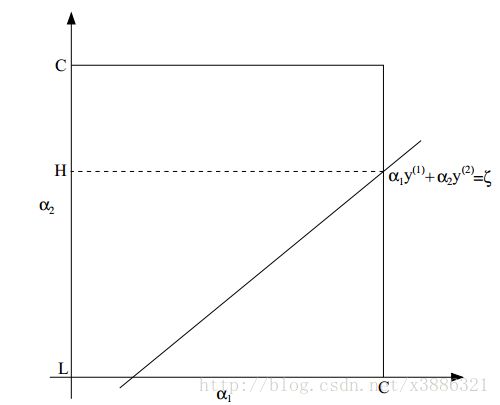
该方法迭代次数较多,但是对于某些能够很快求得arg max的值的问题,该方法的效率很高。那么在SVM问题上,效果如何?老师说,将相关的式子代入到W(a)中,最后会得到一个一元二次函数表达式,同时再加上相应的约束表达式:
![]() (两个参数的相互制约)
(两个参数的相互制约)
![]()
即可很快求得每一次迭代过程中W(a)的最优值。同时,还可以使用一幅图以加深理解:
这就是SMO算法的具体流程。
老师说,到现在算是将机器学习的基础知识学完了,接下来更多的是深入与应用。看来下一篇需要做一个1-8节课的小结了。