机器学习——SVM算法的初识到深入
目录
- 前言
- 初识与了解
- 1.1 线性分类器
- 1.2 逻辑回归
- 1.3 一个简单的线性分类器例子
- 1.4 函数间隔与几何间隔
- 1.5 SVM算法的引出
- 深入与理解
- 2.1 约束方程怎么解(基于线性可分讨论)
- 2.3 线性不可分时
- 2.4 核函数的引入
- 后记
前言
尽管对于SVM算法已有相当多的资料,但大多较为晦涩难懂,要求读者有较高的数理基础及逻辑能力。本文综合参考多本书籍和多篇文章,从浅至深的逐渐讲解SVM算法。一方面是对知识的输出学习,另一方面,旨在能够帮助初学者有更好的理解。
初识与了解
SVM算法属于线性判别的大类别,所以我们需要先了解线性判别的相关概念。
1.1 线性分类器
给定一个样本集 X X X, X = ( x 1 , x 2 , . . . . . . x n ) X=(x_{1},x_{2},......x_{n}) X=(x1,x2,......xn),要求使用线性分类器将其在特征空间内分为两类。 x i x_{i} xi表示第i个样本(数据点), y y y表示标签(例如属于第一类,则 y = 1 y=1 y=1,属于第二类,则 y = − 1 y=-1 y=−1)。而我们最终想要达到的目的是,寻找一个如下的超平面(在n维特征空间中):
w T X + b = 0 w^{T}X+b=0 wTX+b=0
通过数据点相对于超平面的分布情况,从而实现分类。
这里会引出一个问题,为什么标签要给定为-1,1的形式?
事实上,这件事情是与逻辑回归息息相关的,我们接着往下看。
1.2 逻辑回归
逻辑回归的目的是从样本特征里学习出一个0/1分类模型。
那我们对于此做如下探究:
首先,和我们熟悉的线性分类问题相同,逻辑回归学习出的0/1分类模型也是以样本特征的线性组合为输入(因变量)。而不同点在于,我们所熟悉的线性分类问题(狭义)以 g ( x ) g(x) g(x) ,也就是 w T X + b w^{T}X+b wTX+b 为输出的,而0/1模型则通过logistic函数将其对应到一个隐状态 p p p(也就是认为y=1的概率), p = L ( w T X + b ) p=L(w^{T}X+b) p=L(wTX+b)。然后比较 p p p 与 1 − p 1-p 1−p 的值大小(即比较y=1的概率与y=0的概率大小)来决定x的类别。
可以发现,原本取值可以在无穷区间的样本特征的线性组合,在经过逻辑回归的映射函数L后,映射为(0,1)区间内的函数值,映射后的值( p p p)被认为是y=1(也就是属于第一类)的概率。
L函数事实上就是我们熟悉的sigmoid函数,其表达式如下:

图像如下:

可以看到,在L函数下,输出被限制在(0,1)之间,完成了映射关系。
我们令:
h θ ( x ) = g ( θ T x ) = 1 1 + e − θ T x h_{\theta}(x)=g(\theta^{T}x)=\frac{1}{1+e^{-\theta^{T}x}} hθ(x)=g(θTx)=1+e−θTx1
其中 g ( x ) g(x) g(x) 即为sigmoid函数,故我们有如下结论:
P ( y = 1 ∣ x ; θ ) = h θ ( x ) P(y=1|x;\theta)=h_{\theta}(x) P(y=1∣x;θ)=hθ(x)
P ( y = 0 ∣ x ; θ ) = 1 − h θ ( x ) P(y=0|x;\theta)=1-h_{\theta}(x) P(y=0∣x;θ)=1−hθ(x)
推导至此,我们便可以容易看出:当我们要判别某个数据点所属类别时,我们只需要计算它的 h θ ( x ) h_{\theta}(x) hθ(x) 值,若 h θ ( x ) > 0.5 h_{\theta}(x)>0.5 hθ(x)>0.5 ,则 y = 1 y=1 y=1的概率更大,也就是说,将此样本划分到 y = 1 y=1 y=1 类。对应的,若 h θ ( x ) < 0.5 h_{\theta}(x)<0.5 hθ(x)<0.5,则将其划分为 y = 0 y=0 y=0 类。
我们可以看到, h θ ( x ) h_{\theta}(x) hθ(x) 只与 θ T x \theta^{T}x θTx 有关。当 θ T x > 0 \theta^{T}x>0 θTx>0 时, h θ ( x ) > 0.5 h_{\theta}(x)>0.5 hθ(x)>0.5 。当 θ T x > > 0 \theta^{T}x>>0 θTx>>0 时, h θ ( x ) = 1 h_{\theta}(x)=1 hθ(x)=1 。反之, h θ ( x ) = 0 h_{\theta}(x)=0 hθ(x)=0。
如果说我们所希望的是数据点都满足 θ T x > > 0 ( y = 1 ) \theta^{T}x>>0(y=1) θTx>>0(y=1) 和 θ T x < < 0 ( y = 0 ) \theta^{T}x<<0(y=0) θTx<<0(y=0) ,那么逻辑回归就是要学习时正样本的特征远大于0,负样本的特征远小于0的这样一个 θ \theta θ 。
说到这里,似乎已经很接近我们的线性判别了,不同的地方就在于我们的线性判别是以 − 1 / 1 -1/1 −1/1 为类别标签,而逻辑回归则是以 0 / 1 0/1 0/1 作为类别标签。事实上,这并不影响什么,只需要将标签替换,我们就可以得到:
h θ ( x ) = g ( θ T x ) = g ( w T x + b ) h_{\theta}(x)=g(\theta^{T}x)=g(w ^{T}x+b) hθ(x)=g(θTx)=g(wTx+b)
可以看到,如此简单变换后,逻辑回归与线性判别没有任何区别。我们将替换过标签的sigmoid表示如下:
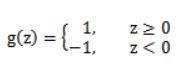
便成为了线性判别中的判别函数,其中 z = θ T x = w T x + b z=\theta^{T}x=w ^{T}x+b z=θTx=wTx+b
1.3 一个简单的线性分类器例子
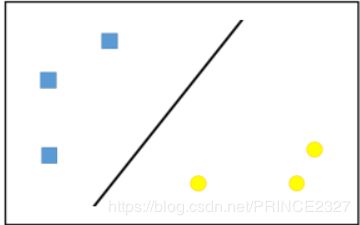
如上图,在二维空间中有两种数据,显然这些数据是线性可分的,所以我们希望寻找到一条直线将这两条数据区分开,这条直线就是我们所说的超平面,可以表示为 f ( x ) = w T x + b f(x)=w ^{T}x+b f(x)=wTx+b。根据上述修改后的sigmoid函数可知: 在超平面一侧 y = 1 y=1 y=1 ,在其另一侧 y = − 1 y=-1 y=−1。如下图:
可以知道,只要知道了超平面,在判断某个模式的类别时,只需要将其带入超平面方程,得到 f ( x ) f(x) f(x),则可判定具体类别。
那么问题很自然地出现了,我们该如何确定这个超平面?有人可能会说,对于某些二类数据分布,随手便可画出无数个超平面(如上图情况)。但是这种想法存在两个问题:
1.当模式特征维数超过3维时我们很难简单地通过肉眼观察。
2.即使可以做到用肉眼观察,那么无数个可行的超平面之间有没有相对比较好的?如果有我们理应去筛选。
基于以上两点讨论,引入一个完整的求解超平面理论是十分必要的。
根据我们的直观感受,我们希望超平面离两类数据点的距离尽量远,这样看起来分类结果足够"保险"(事实上在机器学习里这被称为鲁棒性,换言之也就是系统的抗污染能力)。那么想要提高鲁棒性,就要留有足够的缓存空间以抵抗噪声,这就让我们希望超平面应该距离两类数据簇中距超平面最近的两个数据点距离之和最大,这样在其间隙区域就留有足够的空白区域以缓存干扰,这也就是所谓的SVM算法思想。
很自然地,我们引出了SVM算法。不仅仅是SVM算法,每一种算法背后都有其被引出的原因,希望读者在了解算法的同时也能够知道某种算法的提出背景。
1.4 函数间隔与几何间隔
在正式开始介绍SVM算法之前,我们先引出两个概念:函数间隔与几何间隔。下面我们分别进行简单说明。
根据相关知识,若超平面 f ( x ) = w T x + b f(x)=w^{T}x+b f(x)=wTx+b ,则 ∣ w T + b ∣ |w^{T} + b| ∣wT+b∣ 可以在某种程度上反映模式 x x x 到超平面的远近。通过对于 w T x + b w^{T}x+b wTx+b 以及 y y y 符号的对比,可以判定分类结果是否正确。因此我们可以根据 y ( w T x + b ) y(w^{T}x+b) y(wTx+b)的正负性来判断分类正确性。这也就是我们所说的函数间隔:
对于给定的训练数据集T和超平面 ( w , b ) (w,b) (w,b),定义超平面 ( w , b ) (w,b) (w,b)关于样本点 ( x i , y i ) (x_{i},y_{i}) (xi,yi) 的函数间隔为:
![]()
定义超平面 ( w , b ) (w,b) (w,b) 关于训练数据集T的函数间隔为超平面 ( w , b ) (w,b) (w,b) 关于T中所有样本点 ( x i , y i ) (x_{i},y_{i}) (xi,yi) 的函数间隔之最小值,即:
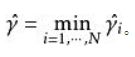
有了如上的函数间隔之后,看起来好像可以根据函数距离去计算找到其最大值时对应的超平面。但事实却非如此,如果成比例地改变 w w w 和 b b b ,那么函数间隔也将改变同等比例,但超平面却没有改变,这意味着对于同一给超平面,可以有无穷大的函数距离,这显然是不现实的,所以我们通过引入一些约束条件从而推导出了几何距离(我们用r表示)。
所谓的约束条件事实上就是对超平面的法向量 w w w 进行约束。
相应推导过程如下:
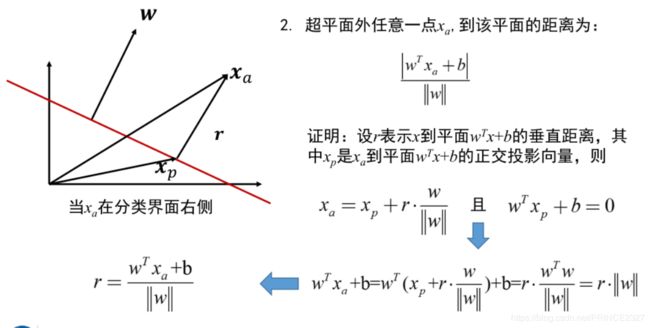
从上述对于两种距离的说明可以看出:函数间隔事实上就是|f(x)|,也就是某个模式点到超平面的竖直距离。而几何间隔是函数间隔除以 ∣ ∣ w ∣ ∣ ||w|| ∣∣w∣∣ ,是我们平常所认知的点到直线距离。
1.5 SVM算法的引出
那么上述讨论让我们知道:
1.我们希望分类结果里数据点到超平面的距离尽量大,这可以有效地提高系统的鲁棒性。
2.而函数间隔并不适用于最大化,因为其可以在超平面固定的情况下取到正无穷。
3.而几何间隔则不同,其除以一个 ∣ ∣ w ∣ ∣ ||w|| ∣∣w∣∣ 作为修正因子,使其大小只随超平面的不同而不同,所以此处最大化距离应该使用“几何间隔”作为测度。
所以我们的目标表达为数学形式就应为:
M a x r Max \ r Max r (其中r为几何间隔)
s . t . y i ( w T x i + b ) = γ i ≥ γ s.t. y_{i}(w^{T}x_{i}+b)=\gamma ^{i}\geq \gamma s.t.yi(wTxi+b)=γi≥γ
其中, γ = r ∣ ∣ w ∣ ∣ \gamma=r||w|| γ=r∣∣w∣∣,故有 r = γ ∣ ∣ w ∣ ∣ r=\frac{\gamma}{||w||} r=∣∣w∣∣γ,为方便推导,我们将 γ \gamma γ 赋值为1,至于为什么要这样做,在文末有相应说明。
从而我们得到新的规划方程:
M a x 1 ∣ ∣ w ∣ ∣ Max \ \frac{1}{||w||} Max ∣∣w∣∣1
s . t . y i ( w T x i + b ) = ≥ 1 s.t. y_{i}(w^{T}x_{i}+b)=\geq 1 s.t.yi(wTxi+b)=≥1
可以看出,这是一个非常漂亮简洁的规划问题,我们通过求解该问题,就可以得到一个距离最大的超平面。

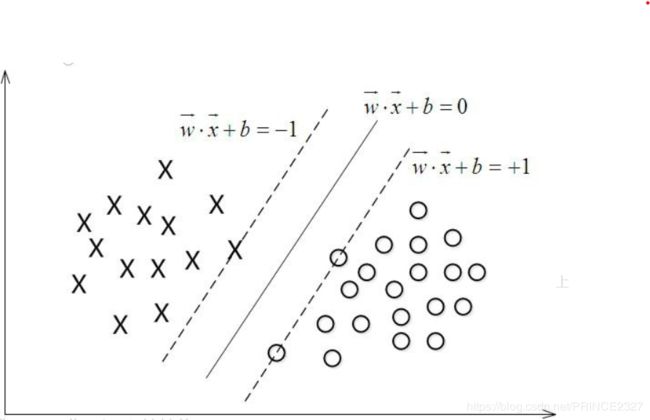
如上图,处在虚线上的一个蓝色点和两个红色点,满足
y i ( w T x i + b ) = 1 y_{i}(w^{T}x_{i}+b)=1 yi(wTxi+b)=1 。看起来就好像是对于平面的支撑,所以这也被称为“支持向量”。以上的分析过程,事实上就完整地引出了SVM算法的思路。
恭喜你,至此,你已经了解了SVM的背景及其思路。如果你希望在日后能够熟练地运用它,第一层已经足以满足你的要求。如果你希望对于SVM算法有更加深入和细致的理解,那么请继续向下看。
深入与理解
上述已经引出了对于SVM算法的约束方程,只要我们求解出最优解,我们就可以得到一个满意的超平面。但是这个“只要”似乎没有说起来那么容易,接下来我们就针对约束方程的解法做以探讨。并且给出各种情况下的SVM算法,最后你会看到,SVM算法在这一套理论体系下显得更加完善和强大。
2.1 约束方程怎么解(基于线性可分讨论)
上述我们已经有了如下最优化问题:
M a x 1 ∣ ∣ w ∣ ∣ Max \ \frac{1}{||w||} Max ∣∣w∣∣1
s . t . y i ( w T x i + b ) = ≥ 1 s.t. y_{i}(w^{T}x_{i}+b)=\geq 1 s.t.yi(wTxi+b)=≥1
似乎很漂亮,但我们希望将其化为更加简单的形式,最好有平方,这样足以抵消很多问题,下面给出具体形式:
M i n 1 2 ∣ ∣ w ∣ ∣ 2 Min \ \frac{1}{2}||w||^{2} Min 21∣∣w∣∣2
s . t . y i ( w T x i + b ) = ≥ 1 s.t. y_{i}(w^{T}x_{i}+b)=\geq 1 s.t.yi(wTxi+b)=≥1
这相对于前面看起来更加漂亮。
在进一步讨论之前,我们先引出一些相关概念。
![]()
凸集:欧氏空间中,对于集合内的每一对点,其连线上的任意一点都落在该集合内。
凸函数:emmmm事实上就是向下凸的函数(更加严格的定定义高等数学中有,这里不做说明)。
引入以上概念后,可以看出,上述的约束问题事实上就是一个凸优化问题,而凸优化问题可以用专用的优化包去解决。虽然如此,但基于此优化问题中结构的特殊性,我们选引入拉格朗日乘子,从而得到一种更有效的解决方法。
具体做法如下:
引入拉格朗日乘子 α \alpha α ,将目标函数与约束方程写在一个式子中:
 令 θ ( w ) = m a x α i ≥ 0 L ( w , b , a ) \theta(w)=max\displaystyle{_{\alpha_{i}\geq 0} }L(w,b,a) θ(w)=maxαi≥0L(w,b,a)
令 θ ( w ) = m a x α i ≥ 0 L ( w , b , a ) \theta(w)=max\displaystyle{_{\alpha_{i}\geq 0} }L(w,b,a) θ(w)=maxαi≥0L(w,b,a)
当约束条件不满足时:存在一项 1 − y n ( w T x n + b ) > 0 1-y_{n}(w^{T}x_{n}+b)>0 1−yn(wTxn+b)>0,此时我们只需要令对应的 α = ∞ \alpha=\infty α=∞ 便可让 θ ( w ) \theta(w) θ(w) 为无穷大。这显然不是我们希望的。
当约束条件都满足时: θ ( w ) = M a x L ( w , b , a ) = 1 2 ∣ ∣ w ∣ ∣ 2 \theta(w)=Max L(w,b,a)=\frac{1}{2}||w||^{2} θ(w)=MaxL(w,b,a)=21∣∣w∣∣2。可以看到,当约束条件全部满足时, θ ( w ) \theta(w) θ(w) 正是我们的目标函数。所以我们进一步可以得到如下形式:

交换顺序后:

根据相关优化理论,有 d ∗ ≤ p ∗ d^{*}\leq p^{*} d∗≤p∗。可以看出,两者并不是完全对等的,而要让式子取等号,则需要满足KKT条件,下面对于KKT条件做以简单介绍。
一般地,一个优化问题可以有如下形式:
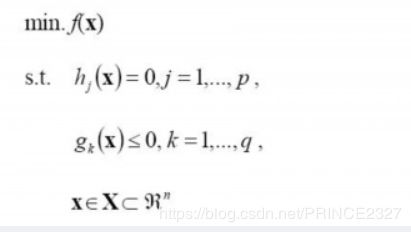
而KKT条件是,对于上述模式中的最小值点 x ∗ x_{*} x∗ 需满足如下式子:
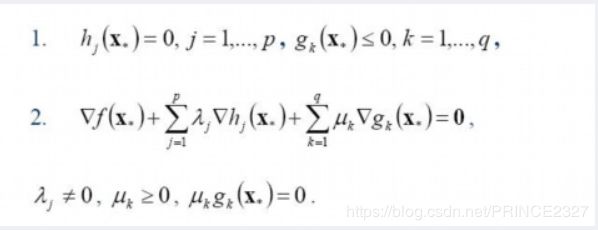
如果满足KKT条件,那么就有 d ∗ = p ∗ d^{*}=p^{*} d∗=p∗成立。原问题又同时满足slater条件并且f与g均可微,故其也满足KKT条件,所以我们可以将其转换到对偶问题上求解。
至此,我们讲述了为什么能够将其转换为对偶问题。接下来就是具体的求解过程,大致分为三个步骤:
(1)固定 α \alpha α,求L关于w,b的最小化问题。
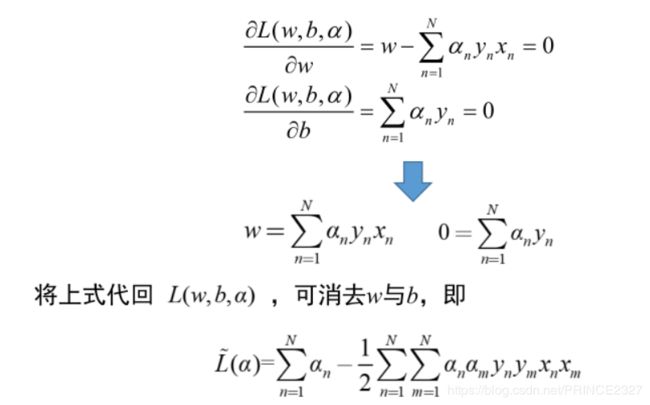
其中推导过程用到了矩阵论的知识,读者如感兴趣可自行尝试推导。
(2)求L对于 α \alpha α 的极大(此时w,b均已用其表示)

(3)求出具体的 α \alpha α
这里采用的是SMO算法,关于SMO算法,这里先不具体讲解,后续博主会更新博客《机器学习——洞悉SMO算法》,届时会详细讲解,欢迎关注。
2.3 线性不可分时
上述讨论均建立在数据线性可分的前提下,但事实上,大多数实际数据都是非线性可分的。下文你将看到,对于线性不可分数据,我们希望将其投影到高维空间中化为线性可分问题,并对其进一步优化从而提出核函数。

上图可以看到,对于原空间中线性不可分的数据,通过某个映射函数可以将其在高维空间中变为线性可分的数据。如此一来就避免了低维空间中复杂的曲线计算。

上图中的 z n z_{n} zn 就是我们所说的映射函数。具体地举一个例子:
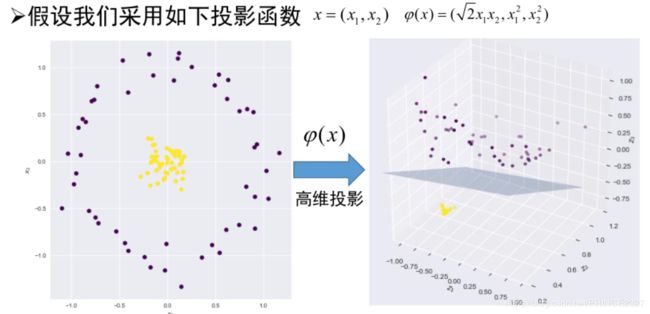
如上图,显然在原空间中我们遇到了线性不可分问题,所以自然地我们想到将其投影到高维空间,那么该如何投影?
根据选取的映射函数,如果原空间中 x = ( a , b ) x=(a,b) x=(a,b),则在高维空间中对应点的坐标为 x = ( 2 1 2 a b , a 2 , b 2 ) x=(2^\frac{1}{2}ab,a ^{2},b ^{2}) x=(221ab,a2,b2)。可以看到,在新空间中,模式变为线性可分的。
故超平面方程由:

变为:
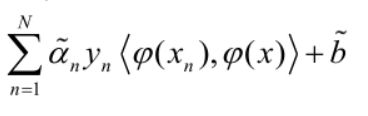
这里 ϕ \phi ϕ 就是非线性映射函数。
这意味着,处理非线性问题应该两步走:
1.使用一个非线性的映射函数 ϕ \phi ϕ 将原样本点映射到高位空间中。
2.在高维空间中使用线性分类方法进行分类。
至此,你看到了SVM处理线性数据与非线性数据的方法,似乎理论体系已经完善。真的是如此吗?我们可以仔细思考以下,上述例子是将二维空间映射到三维空间。如果我们得到的数据集是三位空间呢?我们保证它尽量线性可分,我们将其映射到的新空间的原空间所有维度的一,二,三阶组合,也就是19维空间。可以看到,如此巨大的增长速度势必会给我们带来计算量的剧增。可以看出单单有此理论还是远远不够的,故我们引出了核函数的概念。
2.4 核函数的引入
从一个简单的例子入手:

原本我们要计算高维的超平面时,需要取计算在高维空间中模式的内积,这是让人望而却步的一件事情。但是,我们发现,在低维空间在的内积似乎与高维空间的内积有某种简单的数学关系。如上图,为 C ⟶ C 2 C\longrightarrow C^{2} C⟶C2的映射。
这也就告诉我们,我们确实需要将其映射到高维空间中,但在计算上我们希望能够“投机取巧”,事实上我们确实可以这样做。而这种“投机取巧“的方法就被称为核函数法。

上述即为核函数的定义,核函数也可以被定义为计算两个向量在隐式映射过后的空间中的内积的函数。
上例 C ⟶ C 2 C\longrightarrow C^{2} C⟶C2 的核函数即为:
κ ( x i , x j ) = < x i , x j > 2 \kappa(x_{i},x_{j})=
可以看出,核函数的目的就是简化高维空间中的内积计算,而很美好的一点就是,SVM算法的最终超平面表达式就是以内积形式出现的,所以我们有以下式子:
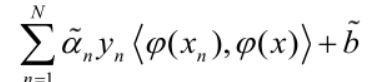
至此,我们说明了核函数的作用,其引入与不引入的区别就是:
1.若不引入,则需直接在高维空间中计算内积,这造成了巨大的计算量。
2.若引入,则我们可以通过在低维空间中计算内积,再通过某种简单的映射关系,从而推导出高维空间中的内积结果。
至此,你已经了解了为什么要引入核函数,下面将介绍几种常见的核函数。
⋅ · ⋅ 线性核
事实上,线性核就是原空间中的内积。引入其主要是为了在形式上统一。通俗地理解,在写算法时,只需要写入此通用表达式,然后代入不同的核即可。
线性核相对来说较为简单,但其应用较窄,对于非线性数据的表现往往不尽人意。
⋅ · ⋅ 多项式核
上述例子即为一个多项式核函数。
⋅ · ⋅ 径向基核
事实上,满足 f ( x ) = f ( ∣ ∣ x ∣ ∣ ) f(x)=f(||x||) f(x)=f(∣∣x∣∣) 的任何函数都可以被称为径向基核,可以看出,其是一个实值函数。
相对来说,径向基核拟合能力强,但也受参数影响大,如果参数选取不恰当,容易引起过拟合。
不同的核函数在分类数据时表现也不同:

至此,你已经了解了常见的核函数类型。如果你尚感觉一头雾水,那么我们对核函数做如下总结:
1.我们往往会遇到非常多的线性不可分数据,此时我们想到将低维数据映射到高维空间中。
2.但是,根据SVM算法的得到超平面表达式,是需要在计算内积的,如果在高维空间中直接进行内积计算,那么势必会造成巨大的运算量。
3.基于以上问题,我们引出了核函数,其价值在于将高维内积运算转换到低维,从而大大简化了计算。
后记
至此,你可以对SVM算法有基本的理解。在后续,博主会持续修改添加更多的内容到其中,进一步完善SVM算法的理论,欢迎关注。

