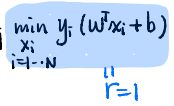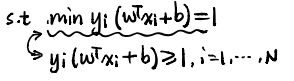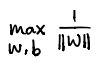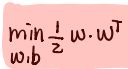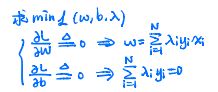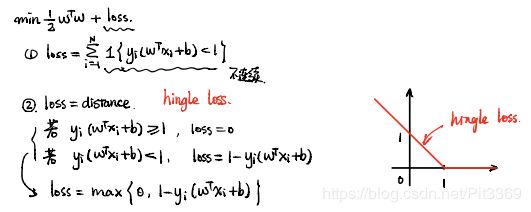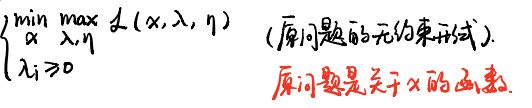SVM支持向量机超详细数学推导过程
感谢哔哩哔哩阿婆主：shuhuai008 、视频讲解：https://www.bilibili.com/video/av28186618/?p=1
SVM有三宝：间隔、对偶、核技巧（核函数）
三个不同的分类算法：hard-margin SVM、soft-margin SVM、Kenel SVM
SVM起初用来解决二分类问题
为何叫SVM支持向量机？及其有关求解实例：https://blog.csdn.net/Pit3369/article/details/88965457
目录
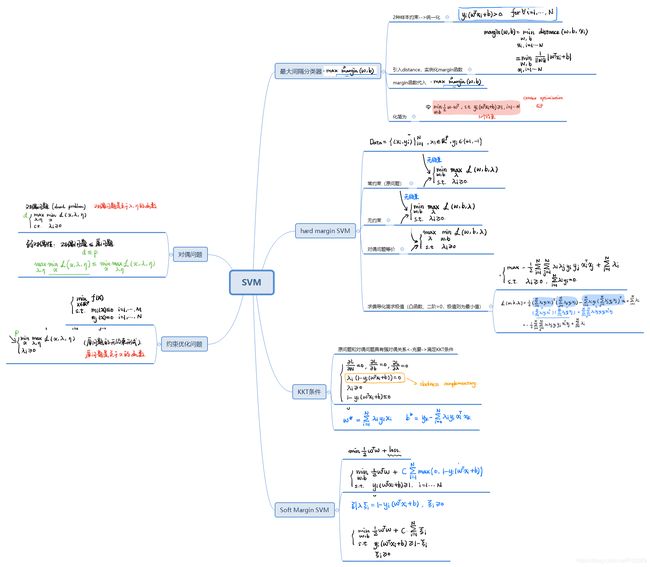
1、hard-margin SVM（硬间隔）---最大间隔分类器（max margin ）
请注意！f(x)=sign(w^T X+b)纯粹是一个判别模型、与概率没有关系！
一、第一步
二、第二步
三、第三步
最终的精髓就是：
P2：硬间隔SVM - 模型求解(对偶问题之引出)
第一步：常约束--->无约束
第二步：无约束问题--->对偶问题
第三步：对偶问题-->求偏导-->进一步化简为无约束问题
P3：硬间隔SVM - 模型求解(对偶问题之KKT条件)
P4---软间隔SVM-模型定义
P5---约束优化+对偶关系证明
约束优化问题（也成为原问题）
对偶问题
1、hard-margin SVM（硬间隔）---最大间隔分类器（max margin ）
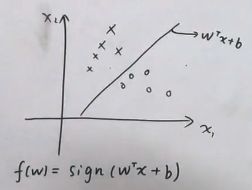
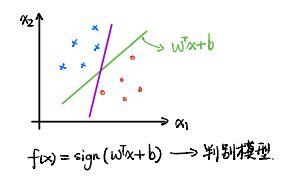
×是一类、圈是一类，找出一个超平面wtx+b=0将此分类。sign是个符号函数，括号内部>0，f(w)为+1；括号内部<0,f(w)为-1。
请注意！f(x)=sign(w^T X+b)纯粹是一个判别模型、与概率没有关系！
其实，
存在许多条超平面可将×与o分类，那么如何找出一个最合适的呢？SVM就是解决此问题的。
什么叫最合适呢？比如那条竖直的超平面，它离o与×距离非常的近，那么它的鲁棒性比较差，容易受到噪音的影响。那么就要找到一个超平面，让它距离两边的距离都足够的大。
推导过程如下：
一、第一步
化简过程：
- xi属于R维立体空间内的点，
二者相乘>0,即就是二者同号，那么就能将s.t.约束中两种情况统一化简为该式。
2.margin是关于超平面的函数，distance是N个点距离该超平面的集合，我们要找出其中的最小值。这里就有疑问？为何要找 出最小值？不应该是找出最大值吗？
其实超平面：距×与o的距离的最小值尽可能地最大化，因为这样的鲁棒性是最好的。
Yi其实包含在Xi内部了，比如二维空间，横坐标X纵坐标Y，也可以写为横坐标X1，纵坐标X2，因为对于N维立体空间，用X1-->Xi表示较为贴切。其实Yi只是一个lable标志，因为随着X1-->Xi的位置不同，Yi只用+1/-1的取值。
||W||表示2范数
二、第二步
化简步骤如下：
1、min是关于Xi的式子，所以可以将(1/||W||)看作常数提至min函数前。
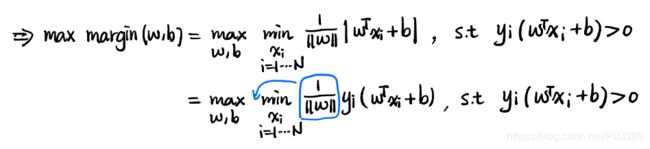2、对于后面的约束S.t，可以找出一个α>0，其值刚好等于该约束。
对于α的值刚好也能取成1，也就是
，也就是
三、第三步
化简过程如下：
==
（其中||W||=W*W^T，但是1/2的出现是为了求导方便引入的）- convex optimization 凸规划的问题
最终的精髓就是：
----推倒为-->
P2：硬间隔SVM - 模型求解(对偶问题之引出)
其中存在一个定理（可以理解是定理）：凸二次规划，极小极大等于极大极小。
推到过程如下：
第一步：常约束--->无约束
上面的凸优化问题，是对w、b带有约束---目标函数和优化条件，可以借助拉格朗日乘数，把问题转化为无约束的问题（对w和b没有了约束，但对λi有约束条件）。这是因为拉格朗日乘子中λi>=0，后面相乘的式子<=0。
注解：
上面的化简，存在隐含的关系式：
，也就是说拉格朗日乘数中λ为自由常数变量，移项后的约束条件
为负。在此情况下，
对应的最大值才是1/2 W^T W的值。
第二步：无约束问题--->对偶问题
宁为鸡头，不做凤尾。其实是一种自我安慰，瘦死的骆驼比马大。凤中凤尾>=鸡中鸡头。
注解：也就是，使得上界最小，下界最大。
第三步：对偶问题-->求偏导-->进一步化简为无约束问题
为了求其最小值，分别对w、b求偏导，解出w和b的值。（此处疑问，为何一阶导为0，解出就是最小值？因为函数是凸函数，凸优化问题，二阶导大于0，所以极值点就是极小值点）
注解：对于第一个式子中，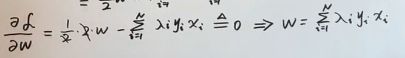
此处就十分准确的体现了为何前面要引入系数1/2.
将偏导=0，解出的关于w、b的式子代入，化简步骤如下：
注解：lambda(i)是一个n维向量。
P3：硬间隔SVM - 模型求解(对偶问题之KKT条件)
注解：
- Slackness complementary 松弛互补条件。S.t为满足条件。
- W*：yi是+1/-1，λi只与支持向量有关，那么W*只是关于data(Xi)的线性组合。
- 对于λi，
，只与那两条+1/-1的线有关系，其余情况下，λi恒为0。
P4---软间隔SVM-模型定义
软间隔：在硬间隔的基础上，允许一点点的错误。
注解：
- hinge loss铰链损失（荷叶损失），横坐标Z，纵坐标loss。当Z>=1时，loss=0；当Z<1时，loss=1-Z。
引入ξi，可进行如下化简：
注解：
表示距离，也就是支持向量距离×/o的长度。如右下角坐标，引入ξi，支持向量距离×/o的长度变化的松弛了，容错率提高了，允许了一些噪声的影响。
P5---约束优化+对偶关系证明
约束优化问题（也成为原问题）
注解：
- 此处的无约束指的是，针对于原问题的mi(x)、mj(x)没有过多的限制，只是对λ做出了S.t
注解：
- 好的x指的是，满足mi(x)<=0的那些x集合，坏的x指的是，不满足mi(x)<=0(也就是mi(x)>0)的那些x集合。
- 对于x违反了约束mi(x)的那些，为何会使得max(λ)L->+∞？λ是常数，对于mi(x)尽可能的大时，Σ就会使得无限接近∞
对偶问题
原问题：
对偶问题：
弱对偶性的证明：
