机器学习与线性回归

   线性回归（Linear Regression) 是机器学习的一个很基础很简单的模型了，但它的地位却非常重要，很多时候常用于预测、分类等任务中。先放一张图片来直观地感受一下线性回归。（事实上线性回归学习出来的模型不一定是直线，只要变量是1维的时候才是直线，高维的时候是超平面）。

   线性模型（Linear Model) 的基本形式为：
   给定由d个属性描述的示例x = (x₁;x₂;…;x_n)，其中x_i是x在第i个属性上的取值，线性模型试图通过学习得到一个通过属性的线性组合来进行预测的函数，即： h(x) = θ₁x₁ + θ₂x₂ + … +θ_dx_d + b
   为了方便表述，用向量的形式写出来： h(x) = θ^Tx + b, 其中θ = (θ₁;θ₂;… ;θ_d)。 θ和b学得之后，模型便得以确定。为了进一步简化，在上式中加入x₀，则可以最终得到h(x) = θ^Tx。
  为了确定θ，关键在于衡量h(x) 与 y 之间的区别。则均方误差是回归任务中最常用的性能度量，因此可以试图让均方误差最小化，那么基于均方误差最小化来进行模型求解的方法则称为“最小二乘法“(least square method)，在线性回归中，最小二乘法就是试图找到一条直线，使得所有样品到直线上的欧氏距离最小。那么求解θ使得其均方误差最小化的过程，称为线性回归模型的最小二乘”参数估计”。
   在m个样本中，有上述可得其一个比较“符合常理”的误差函数为(最小二乘建立的目标函数，即噪声为均值为0的高斯分布下，极大似然估计的目标函数）：

J(θ)=12∑mi=1(hθ(x(i)−y(i))2

公式中x ⁽ⁱ⁾是估计的第i个, y ⁽ⁱ⁾则是实际上的第i个的值。
  在线性回顾中，可以写成 y ⁽ⁱ⁾ = θ ^T x ⁽ⁱ⁾, 事实上还存在有噪声的影响，那么用ϵ ⁽ⁱ⁾来表示噪声（ θ ^T x ⁽ⁱ⁾得出来的往往离实际上的 y ⁽ⁱ⁾还有一定的距离，故要加上 ϵ ⁽ⁱ⁾），此时得出的公式即为： y ⁽ⁱ⁾ = θ ^T x ⁽ⁱ⁾ + ϵ ⁽ⁱ⁾。由于各个噪声 ϵ都是独立分布，互不影响的，故其符合高斯分布，此时它的均值为0，设其方差为 σ ²，则其似然函数为：

p(ϵ(i))=12π−−√σexp(−(ϵ(i))22σ2)

  进一步可以写成：

p(y(i)x(i);θ)=12π−−√σexp(−(y(i)−θTx(i))22σ2)

  最终可得到似然函数为 :

L(θ)=∏mi=1p(y(i)|x(i);θ)=∏mi=112π−−√σexp(−(y(i)−θTx(i))22σ2)

  为了计算简便，我们对上一条公式进行取对数，得到的对数似然函数为：

l(θ)=lnL(θ)=∑mi=1ln12π−−√σexp(−(y(i)−θTx(i))22σ2)=mln12π−−√σ−12σ2∑mi=1(y(i)−θTx(i))2

  要求的最适合的θ，即是使得造成的误差最小，也就是要求求出使得l(θ)函数取最小值时候的θ， 求解过程中，我们可以对其进行求梯度（求导)：

∇θJ(θ)=∇θ12(Xθ−y)T(Xθ−y)=12∇θ(θTXTXθ−θTXTy−yTXθ+yTy)=12(XTXθ+XTXθ−2XTy)=XTXθ−XTy

  令上公式为0得：

θ=(XTX)−1XTy

若X ^TX不可逆，则：

θ=(XTX+λI)TXTy

  此时所求出的结果是全局最优的。 当X ^TX不可逆时，为什么加入了一个单位矩阵，这里做出一下证明：设X ^TX是半正定的，对于任意的非零向量u，有： u ^TX ^TXu = (u ^TX ^T)(Xu)，令v = Xu，则可得v^Tv ≥ 0， 所以，对于任意的实数λ > 0 加入后，X ^TX + λI正定，从而可逆。此外，若X ^TX劫数过高的话，需要进行梯度下降。那么下面来看一下梯度下降的算法：

• 初始化θ（随机初始化）
• 迭代，新的θ能够使得J(θ)更小
• 如果J(θ) 能够继续减小，则返回步骤2，不断重复直到θ收敛。基本公式为：
  θj:=θj−α∂∂θjJ(θ)
  
    其中上式中的α为学习率或者步长；继续求解得：
  ∂∂θjJ(θ)=∂∂θj12(hθ(x)−y⃗ ）2=2∗12(hθ(x)−y⃗ )2∗∂∂θj(hθ(x)−y⃗ )=(hθ(x)−)∂∂θj(∑ni=0θixi−y⃗ )=(hθ(x)−y⃗ )xj
  
    事实上这也叫作批量梯度下降法(Batch gradient descent)，这里放上一张图可以更加直观的看出来。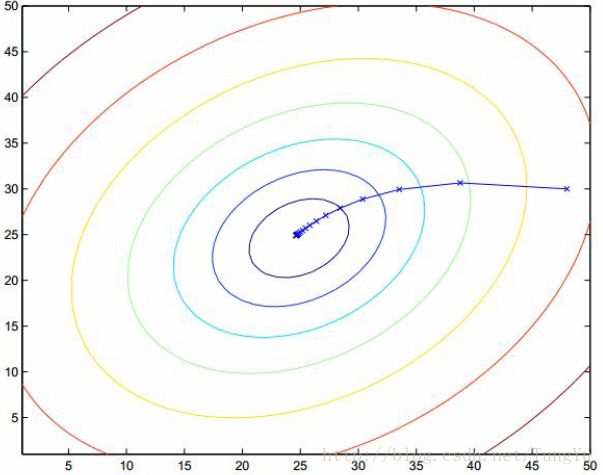
    事实上通过BGD所得出的θ一定是最优解，但与此同时缺点就是计算代价大、花费时间长，毕竟BGD要把所有的样本运算一遍才可以，所以，就又有一个随机梯度下降法(Stochastic gradient descent)。而SGD则是更为常用。SGD每次从训练集中随机选择一个样本来进行学习，即：
  θj:=θj+α(y(i)−hθ(x(i))x(i)j
  
  BGD每次都会使用全部训练样本，因此这些计算是冗余的，因为每次都使用完全相同的样本集。而SGD每次只随机选择一个样本来更新模型参数，因此每次的学习是非常快速的，并且可以进行在线更新。由于SGD通过每个样本来迭代更新一次，如果样本量很大得情况下，可能只用几千、几万得样本就可以达到最优解了。但是问题来了，SGD的噪声比BGD的多，因此并不是每次迭代的方向都朝着最优的方向，但效率却提高了。SGD得出的不一定是最优解，但一定在最优解的附近。下面一张图则是对SGD的一个直观的描述：
  
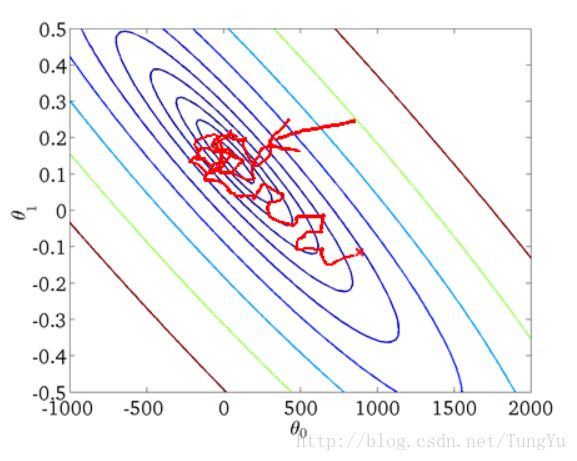
    在对BGD和SGD两个算法作一个折中后，便是mini-batch梯度下降算法了，它不是每拿到一个样本即更改数据，而是若干个样本的平均梯度作为更新方向，这样做效率高的同时又可以做到比SGD的结果更优。那么梯度下降的具体过程到底是怎样的呢？请看下面：
• x_k = a，沿着负梯度方向，移动到x_k+1 = b， 有：
  b=a−α∇F(a)⟹f(a)>f(b)
• 从x₀为出发点，每次沿着当前函数梯度反方向移动一定距离α_k， 得到序列：
  x0,x1,...,xn
• 对应的各点函数值序列之间的关系为：
  f(x0)≥f(x1)≥f(x2)≥...≥f(xn)

• 当n达到一定值时，函数f(x) 收敛到局部最小值，由于函数本身是凸函数，所以局部最小值即是全局最小值，则此时得到的θ是我们想要的。

    上面的式子中都会用到α这个东西，前面耶解释过，α是指学习率或者步长，那么α应该如何确定和优化呢？下面将会介绍几种方法。首先很明显的一个点就是在方向导数大的地方用小的学习率，方向导数小的地方用大的学习率，这是毋庸置疑的。然后要怎么求解更加合适的学习率呢？首先记当前点为x_k，当前搜索方向为d_k（如：负梯度方向），因为学习率α是待考察对象，因此，将函数f(x_k+αd_k)看作是关于α的函数h(α)。即：

  h(α)=f(xk+αdk)，α>0
  
    其导数为：
  ∇h(α)=∇f(xk+αdk)Tdk
  
    那么α的计算标准为：因为梯度下降是寻找 f(x)的最小值，那么在x_k，d_k给定的前提下，即寻找f(x_k + αd_k)的最小值，即：
  α=argmin(α>0)h(α)=argmin(α>0)f(xk+αdk)
  
    若h(α)可导，则局部最小值处的α满足：
  h′(α)=∇f(xk+αdk)T
  
    若学习率最优，则必定会满足其偏导等于0:
  h′(α)=∇f(xk+αdk)Tdk=0
  
    下面对学习率函数导数做一下分析：

• 将α = 0带入：

  h′(0)=∇f(xk+0∗dk)Tdk=∇f(xk)Tdk

• 下降方向d_k可选择负梯度方向：d_k = -∇f(x_k) ;
• 从而使得： h’(0) < 0;

• 如果能够找到足够大的α， 使得h’(α) > 0, 则必存在某α，使得h’(α) = 0, α即为要寻找的学习率。

    求解α最简单的方法则是二分线性搜索（Bisection Line Search )，这个方法与求解方程的解的夹逼法很相似。二分线性搜索即是不断将区间[ α₁, α₂ ]分成两半，选择端点异号的一侧，直到区间足够小或者找到当前最优学习率。
    此外，还有一种方法叫做回溯线性搜索（Backing Line Search ) 。这是基于Armijo准则（什么是Armijo准则呢？参见这个博客的解释，非常有道理： 解释Armijo准则 )计算搜索方向上的最大步长（学习率），其基本思想是沿着搜索方向移动一个较大的步长估计值，然后以迭代的形式不断缩减步长，直到该步长使得函数值 f(x_k)的减小程度大于预设的期望值（即满足Armijo准则）为止，此时的步长则为最优的学习率。计算表达式为：

  f(xk+αdk)≤f(xk)+c1α∇f(xk)Tdk,c1∈(0,1)
  其中c₁α∇f(x_k)^Td_k一般为负值，式子的意思就是说，旧的函数值f(x_k)减去一个数，还是比新的函数值f(x_k + αd_k)大。
    那么二分线性搜索和回溯线性搜索有何异同呢？二分线性搜索是求得满足h’(α) ≈ 0 的最优α的近似值；而回溯线性搜索则放松了对α的约束，只要α能使函数值有足够大的变化就可以。前者可以减小下降的次数，但计算花费的代价大；后者则是找到一个差不多的α即可。
    接下来便是如何用代码来实现线性回归模型了。这里面用的数据集是一个简单的二维数据集，其截图如下：

  

我们先用python来实现一遍批量梯度下降法：

import pandas as pd
import numpy as np

#读取数据集并分割数据集
data_s = pd.DataFrame(pd.read_csv('E:ex0.csv'))
x = np.array(data_s['X'])
y = np.array(data_s['Y'])

threshold = 0.1  #迭代阈值，当两次迭代函数之差小于该阈值便停止迭代
alpha = 0.98  #学习率
loop_max = 10000  #最大迭代次数，防止死循环

#初始化参数数
theta_0 = 0
theta_1 = 0
time_lteration = 0  #初始化迭代次数为0
m = len(x)
diff = 1  #初始化残差
error1 = 0  #初始化损失
error0 = 0  #初始化损失

while time_lteration < loop_max:
    time_lteration += 1
    k = 0
    l = 0
    for i in range(m):
        h = theta_0 + theta_1 * x[i]
        k += (y[i] - h) * x[i]
        l += (y[i] - h)
    theta_1 += alpha * k /m
    theta_0 += alpha * l /m

    for i in range(m):
        error1 += (y[i] - (theta_0 + theta_1 * x[i])) ** 2 / 2
        if abs(error1 - error0) < threshold:
            break
        else:
            error0 = error1
            print("theta_0: %f,   theta_1: %f,   error1: %f" % (theta_0, theta_1, error1))
print('Done: theta_0: %f,   theta_1: %f' % (theta_0, theta_1))
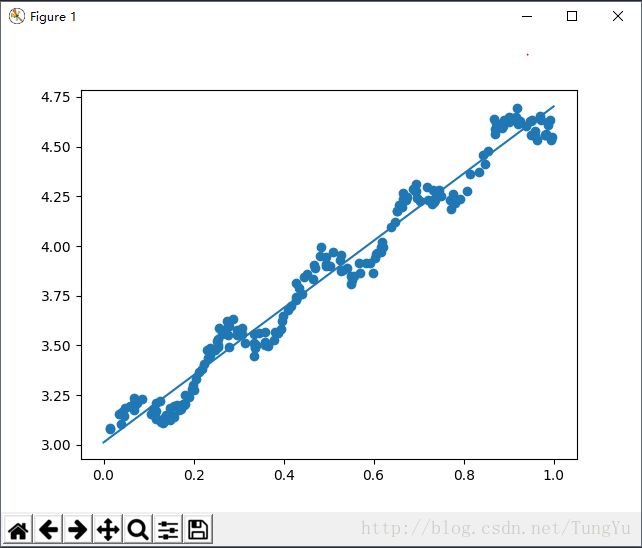
print(time_lteration)

  运行结果为：

然后在把这条曲线画出来和原本数据集画出来的散点图进行对比，运行效果如下：

  可见拟合的效果还是很不错的，上面用到的是批量梯度下降算法，这个数据集还不是很大，所以运行起来很快就得出了结果，下面来看一下随机梯度下降法的实现，数据集还是用上面的数据集。python代码如下：

import pandas as pd
import numpy as np

#读取数据集并分割数据集
data_s = pd.DataFrame(pd.read_csv('E:ex0.csv'))
x = np.array(data_s['X'])
y = np.array(data_s['Y'])

threshold = 0.00001  #迭代阈值，当两次迭代函数之差小于该阈值便停止迭代
alpha = 0.002  #学习率
loop_max = 10000  #最大循环次数，防止死循环

#初始化参数数
theta_0 = 0
theta_1 = 0
time_lteration = 0  #初始化迭代次数为0
m = len(x)
diff = [0]  #初始化残差
error1 = 0  #初始化损失
error0 = 0  #初始化损失
while time_lteration < loop_max:
     time_lteration += 1
#参数迭代计算
     for i in range(m):#拟合函数为：y = theta_0 * x_0 + theta_1 * x 其中x_0 = 1；
         diff[0] = (theta_0 + theta_1 * x[i]) - y[i]  #计算残差
         theta_0 -= alpha * diff[0]
         theta_1 -= alpha * diff[0] * x[i]

     error1 = 0
     for n in range(len(x)):
         error1 += (y[n] - (theta_0 + theta_1 * x[n]))**2 / 2  #最小二乘法

     if abs(error1 - error0) < threshold:
         break
     else:
         error0 = error1
         print ("theta_0: %f,   theta_1: %f,   error1: %f" %(theta_0, theta_1, error1))
print ('Done: theta_0: %f,   theta_1: %f' %(theta_0, theta_1))
print (time_lteration)

运行效果如下：

然后在把这条曲线画出来和原本数据集画出来的散点图进行对比，运行效果如下：

对比两者发现效果还是不错的，虽然上面的批量梯度下降法有点小问题，但总体还是算好了。现在算法实现了，那么就用这个算法来进行预测鲍鱼的年龄。其中关于鲍鱼年龄的数据集截图如下：

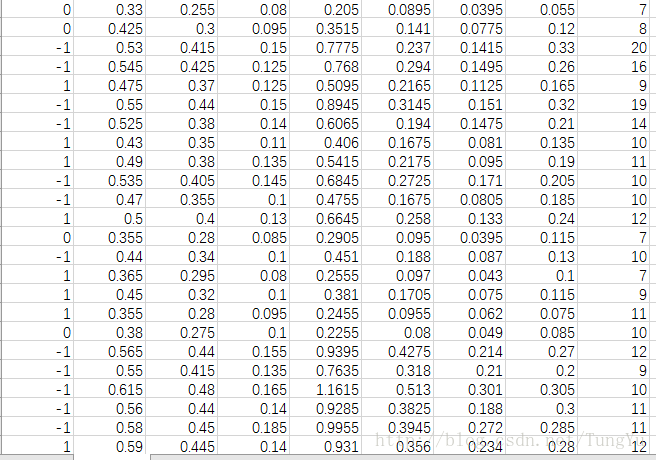
  然后把之前实现的算法加进去。由于线性回归中还有可能会存在偏移量，故在数据集前面加上常数1。线性回归的源代码如下:

import pandas as pd
from numpy import *
import numpy as np

'''
拟合函数可以表示为：y =theta_1 +  theta_2 * X_1 + theta_3 * X_2 + theta_4 * X_3 + theta_5 * X_4 + theta_6 * X_5 + theta_7 * X_6 + theta_8 * X_7 + theta_9 * X_8
平方误差可表示为： 实际值减去预测值的平方和， 由于当误差为0时，theta可以取得最优解，故对误差公式求导化简可得theta的最优解
              等于X的转置矩阵乘以X求逆然后再乘以X的转置矩阵最后乘以y，所以算法的实现如下：
'''
#读取数据集
data_s = pd.DataFrame(pd.read_csv('E:abalone.csv'))
#设置目标值和特征值
X = np.array((data_s[['X_1', 'X_2', 'X_3', 'X_4', 'X_5', 'X_6', 'X_7', 'X_8', 'X_9']]))  #其中X_1是添加上去的1，用来计算偏移量
Y = np.array((data_s['Y']))

#建立计算theta的函数
def SoluteCoefficient(X, Y):
    X_Mat = np.mat(X)   #把数据类型转化为矩阵
    Y_Mat = np.mat(Y).T   #把数据类型转化为矩阵并转置
    xTx = X_Mat.T * X_Mat
    if linalg.det(xTx) == 0.0:   #检测行列式是否为0
        print ("Loooooooose!!!!!!")
        return
    else:
        thetas = xTx.I * (X_Mat.T * Y_Mat)   #计算并获取theta
        return thetas

thetas = SoluteCoefficient(X, Y).T

运行后，运用Numpy库提供的相关系数计算方法：即通过corrcoef（yEstimate， yActual）来计算预测值和真实值的相关性。运行结果如下：

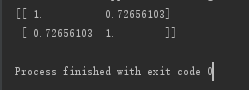
  该矩阵的意思为两两组合的相关系数，都为1的对角线表示的是Y自身与自身的相关系数，故为1；而计算出来的thetas和X相乘后得出来的结果和Y的相关系数却非常低，即出现了所说的欠拟合现象，所以接下来就要用到局部加权线性回归（Locally Weight Liner Regression)的思想。LWLR即是指给待预测的每个点都赋予一定的权重，然后在每个子集都基于最小均方差来进行普通的回归，这种算法需要事先选取出对应的数据子集。其算法的过程的主要流程如下

1. fit θ to minimize ∑_i(y⁽ⁱ⁾−θ^Tx⁽ⁱ⁾)²
2. output θ^Tx
3. fit θ to ∑_iw⁽ⁱ⁾(y⁽ⁱ⁾−θ^Tx⁽ⁱ⁾)² （w⁽ⁱ⁾为权值）

4. output θ^Tx （此为求出的局部加权）

     关于w的设置，通常使用高斯核函数：

   wi=exp(−(x(i)−x)22τ2)
   
     其中τ为带宽，即控制着训练样本随着与x⁽ⁱ⁾距离的衰减速率。τ的选择非常重要，如果过小，则可能会造成欠拟合，过大可能会造成过拟合，故需要根据实际情况而定。下面的一张图片可以形象地说明了局部加权线性回归的拟合效果：
   
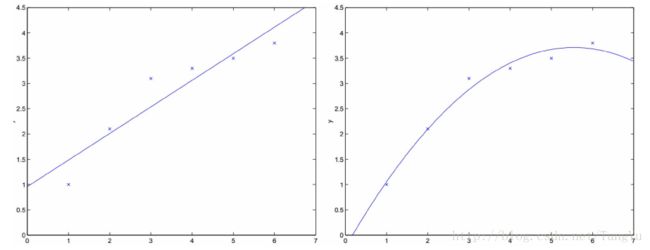
     下面用代码来实现一下局部线性回归的算法：

import pandas as pd
from numpy import *
import numpy as np

def LWLR(points, x_array, y_array, k = 1.0):
    x_mat = mat(x_array)
    y_mat = mat(y_array).T
    h = shape(x_mat) [0]  #查看矩阵或者数组的维数
    weights = mat(eye((h)))  #建立以h为维度的单位矩阵
    for i in range(h):
        qu_mat = points - x_mat[i, :]
        weights[i, i] = exp(qu_mat * qu_mat.T / (-2.0 * k ** 2)) #高斯核函数
    xTx = x_mat.T * (weights * x_mat)
    if linalg.det(xTx) == 0.0:    #检测行列式是否为0
        print ('looooose!!!')
        return
    else:
        thetas = xTx.I * (x_mat.T * (weights * y_mat))
    return points * thetas

  把数据集放进去：

import pandas as pd
from numpy import *
import numpy as np

def LWLR(points, x_array, y_array, k = 1.0):
    x_mat = mat(x_array)
    y_mat = mat(y_array).T
    h = shape(x_mat) [0]  #查看矩阵或者数组的维数
    weights = mat(eye((h)))  #建立以h为维度的单位矩阵
    for i in range(h):
        qu_mat = points - x_mat[i, :]
        weights[i, i] = exp(qu_mat * qu_mat.T / (-2.0 * k ** 2)) #高斯核函数
    xTx = x_mat.T * (weights * x_mat)
    if linalg.det(xTx) == 0.0:
        print ('looooose!!!')
        return
    else:
        thetas = xTx.I * (x_mat.T * (weights * y_mat))
    return points * thetas

def LWLR_test(test_array, x_array, y_array, k = 10.000):   #用于为数据集中的每个元素调用LWLR函数，计算每个样本点对应的权重值
    n = shape(test_array) [0]
    y_Cal = zeros(n)  #生成全零数组
    for j in range(n):
        y_Cal[j] = LWLR(test_array[j], x_array, y_array, k)
    return y_Cal

def wucha(Y, Y_jia):   #计算误差
    return sum((Y - Y_jia) ** 2)

#读取数据集
data_s = pd.DataFrame(pd.read_csv('E:abalone.csv'))
#设置目标值和特征值
X = np.array((data_s[['X_1', 'X_2', 'X_3', 'X_4', 'X_5', 'X_6', 'X_7', 'X_8']]))
Y = np.array((data_s['Y']))
Y_jia = LWLR_test(X[100:199], X[0:99], Y[0:99], 10)
a = wucha(Y[100:199], Y_jia.T)
print (a)

  最后运行得出的结果如下：

  可见运行效果还是可观的。
  线性回归是回归思想的一个基础但是又很重要的部分，但只是其中的一部分，在广义的线性回归上还会有logistic回归、对数线性模型等等，还有树回归等各种各样的内容，等日后有时间再一一补上好了~