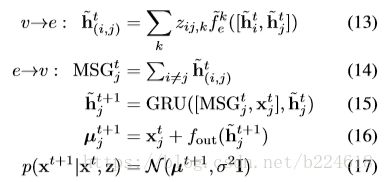读书笔记13:Neural relational inference for interacting systems(ICML 2018)
文章地址:https://arxiv.org/pdf/1802.04687v1.pdf
摘要部分:摘要的结构和前几篇依然类似,首先是介绍背景:interacting system在自然界中普遍存在,各个组成部分之间的相互作用会引发复杂的行为。然后介绍自己的模型:我们提出了neural relational inference(NRI)模型,是一个无监督的模型,学习相互作用的同时还能仅仅从观察的数据学习出整个系统的动力学变化(dynamics)。我们的模型的形式是一个变异的auto-encoder,latent code表示潜在的相互作用图(interaction graph),reconstruction是基于graph neural network的。最后介绍了实验结果,在模拟物理体系的实验中,NRI以一种非监督的形式,精确的复现真实的相互作用,我们还证明了我们可以找到一个可解释的结构并基于真实的运动数据来预测复杂的动力学过程。
最近这几篇学习笔记都分析了摘要的结构,发现其实在大体结构都是背景——模型简介——实验结果,在模型简介的时候,可以有两方面可以写,一方面是每一篇都有的,是模型的特性、能力、特征,但是不涉及到模型的工作方式,例如本文中说模型是非监督的、能够在学习相互作用的同时学习动力学演化;另一方面就是模型大致的工作方式,例如本文中介绍模型是auto-encoder的变体,latent code表示interacting graph这一部分。介绍模型工作过程又分两种,一种是模型简单,一句话就能把工作过程的核心讲清楚,例如non-local neural network那篇,直接就说了模型的工作方式是计算每一个位置响应的时候是通过对所有位置的特征加权求和得到的。另一种就是模型复杂,一句话讲不清,看了还是不是很清楚具体操作方式,例如本文的介绍(也可能是我背景知识不够所致,但是应该还是有些文章是因为本身结构复杂,一两句话讲不清让人看不懂的),可能只是介绍了模型的几个主要方面,但是这些东西是如何串起来的,还有没有什么细节和没提到的模块,还不得而知。
introduction部分:第一段还是简介背景,很多实际问题都可以表示成相互作用的组成部分构成的graph,引发组成部分的复杂运动和系统层面的复杂行为。我们经常只有每个个体的轨迹信息,而没有相互作用信息或者动力学模型,因此这些系统的模拟格外困难。第二段给出了一个具体的例子,说是在篮球比赛中,我们人类可以通过观察球员的运动来很好的判断可能发生的不同相互作用。给定一个任务以后,手动标注一些相互作用可能虽然繁琐但是是可行的,但是以一种非监督的方式学习相互作用,是更加有前途的,并且能够推广到多种情况中。第三段介绍的是现有模型的状况,处理相互作用系统的运动模型可以被视作在全连接的graph上传递信息的graph neural network,interaction的模拟要么是通过message passing function,要么就是用attention机制来实现。第四段就是介绍自己的工作的了,介绍自己的工作可以学习explicit interaction结构(这个explicit和implicit经常出现,一直不是很理解是什么意思),同时也能以一种非监督学习的方式学习相互作用系统的动力学模型(应该就是运动相关的信息)。之后还是和摘要中说的差不多,提到模型是用GNN在一些离散的latent graph上学习动力学,并且在latent variables上进行推断。最后还有几句话也是很概括的介绍模型,说推断出来的edge对应相互作用的clustering,使用概率模型使我们能够有原则的将prior belief包含进graph structure里面,比如sparsity,看不太懂,还是看后面的具体介绍吧。最后一段还是介绍实验。
其实introduction和abstract的结构基本一样,前两段介绍背景,第三段介绍当前的工作,然后介绍自己的模型,最后介绍实验。
本文没有related work,取而代之的是background,主要介绍的是graph neural networks。
然后介绍技术部分,模型分两个部分,一起训练,一个是encoder,基于给定的object的运动轨迹来预测interaction,另一个是decoder,通过interaction graph来学习dynamical model,模型的输入包含N个object,![]() 表示t时刻所有object的feature vector,object i的轨迹就是
表示t时刻所有object的feature vector,object i的轨迹就是![]() ,可见这个feature vector指的是坐标,要么就是将trajectory轨迹的含义推广了,不一定是坐标空间里的轨迹(这种说法感觉靠谱)。作者假设随便给一个graph z,
,可见这个feature vector指的是坐标,要么就是将trajectory轨迹的含义推广了,不一定是坐标空间里的轨迹(这种说法感觉靠谱)。作者假设随便给一个graph z,![]() 表示object v_i和v_j之间的离散的edgetype,而本文的任务就是同时学习去预测edge type以及学习运动模型(dynamical model)in an unsupervised way。整个模型的结构如下:
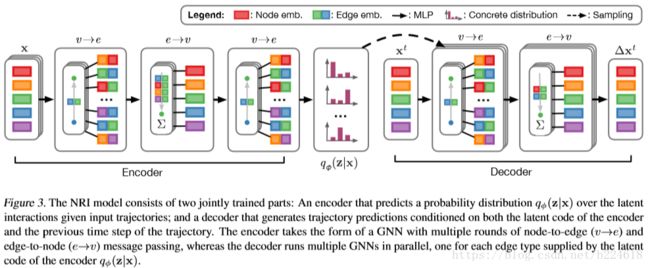
表示object v_i和v_j之间的离散的edgetype,而本文的任务就是同时学习去预测edge type以及学习运动模型(dynamical model)in an unsupervised way。整个模型的结构如下:
左边是encoder,右边是decoder,encoder根据输入的x预测一个隐藏的interaction graph的概率分布,这个就是模型所预测的相互作用的结果,然后decoder再根据这个相互作用的概率分布以及之前时刻的轨迹输出下一步轨迹的预测。具体介绍encoder和decoder,首先,encoder是![]()
![]() ,由于一开始不知道object之间的相互作用情况,所以使用的interaction graph是一个全连接的graph,
,由于一开始不知道object之间的相互作用情况,所以使用的interaction graph是一个全连接的graph,![]() 就是用来在这个全连接的graph上进行操作的graph neural network。假设给定了object的轨迹是1到K的
就是用来在这个全连接的graph上进行操作的graph neural network。假设给定了object的轨迹是1到K的![]() ,encoder计算方式如下:
,encoder计算方式如下:
这里面的f全都是神经网络,要么就是MLP,要么就是1维的CNN。公式(5)展示的是先用一个神经网络处理一下原始的输入,进行一下embedding,公式6就是根据处理过后的结点的信息生成一些edge的特征,是结点信息流向edge,公式7中信息又从edge流向vertex(结点),每一个节点都获得一个由所有与其相连的edge的信息生成的特征,由于graph此时是全连接的,因此这一步其实是每一个节点都获得了整个graph各个部位的信息,之后公式8又将vertex信息传递给edge,在这个模型中,edge的信息![]() 不再像其他GNN一样只起到输运信息的作用,而是graph的一个重要的组成成分。最终encoder的输出是
不再像其他GNN一样只起到输运信息的作用,而是graph的一个重要的组成成分。最终encoder的输出是![]()
![]() 。这个函数将信息在edge和vertex之间来回传递,是为了能够在只进行两两之间的计算的时候能够抓取multiple interaction(指的应该是多体之间的相互作用,看后面解释其实就像是扩大了感受野一样),例如公式6只用了两个节点的信息,而公式7用到的就是整个graph的信息了,因为公式6已经将所有节点的信息传递给了edge。
。这个函数将信息在edge和vertex之间来回传递,是为了能够在只进行两两之间的计算的时候能够抓取multiple interaction(指的应该是多体之间的相互作用,看后面解释其实就像是扩大了感受野一样),例如公式6只用了两个节点的信息,而公式7用到的就是整个graph的信息了,因为公式6已经将所有节点的信息传递给了edge。
decoder是![]() ,用来预测系统进一步的运动状况,这一步是处理graph,因此一般来讲可以使用任何一种GNN来进行这个操作。模拟物理系统的时候,动力学过程是一个马尔科夫过程,
,用来预测系统进一步的运动状况,这一步是处理graph,因此一般来讲可以使用任何一种GNN来进行这个操作。模拟物理系统的时候,动力学过程是一个马尔科夫过程,![]() ,如果状态是位置和速度,z是ground-truth graph(应该指的就是那个interaction graph)。decoder的具体工作过程如下
,如果状态是位置和速度,z是ground-truth graph(应该指的就是那个interaction graph)。decoder的具体工作过程如下
![]() 是vector z_ij的第k个元素,
是vector z_ij的第k个元素,![]() 是一个固定的方差,并且注意,由于有
是一个固定的方差,并且注意,由于有![]() 的加入,模型学习的是
的加入,模型学习的是![]() 的变化量
的变化量![]() 。有的时候系统的变化不是马尔科夫过程,这个时候模型的更新方式是
。有的时候系统的变化不是马尔科夫过程,这个时候模型的更新方式是
这里,message passing的输入是前一个时刻的hidden state,而且这里有了一个edge的hidden state是由node的hidden state来决定的,这使得每一个时刻的信息都可以通过hidden state一直向下传递,这种形式可以使得t+1时刻的预测不仅基于上一时刻,而是基于之前所有时刻的信息。每一次更新的时候,先是由上一时刻的节点的hidden state来更新edge的hidden state,然后为node j的更新准备一个MSG,方式是将所有与其相连的edge的hidden state相加,之后,将node j当前的观察值,MSG,和当前的hidden state输入GRU得到下一时刻的hidden state,再由前一时刻观察值和当前时刻的hidden state预测下一时刻状态(位置速度等量)的分布。
前面提到本文的模型是变分auto-encoder(variational auto-encoder)并不仅仅是说本文的模型基于aotu-encoder,variational encoder(VAE)是具体指一类特定的模型(Auto encoding variational bayes和Stochastic backpropagation and approximate inference in deep generative models),这种模型的目标是最大化![]() 。这里面有两项:一个是reconstruction loss,
。这里面有两项:一个是reconstruction loss,![]() ,第二项是非对称的,信息的理论衡量标准,衡量两个分布之间相似度的KL divergence,
,第二项是非对称的,信息的理论衡量标准,衡量两个分布之间相似度的KL divergence,![]() =
=![]() (参考自http://edwardlib.org/tutorials/klqp)深入理解这个还需要专门去学习一下相关知识。
(参考自http://edwardlib.org/tutorials/klqp)深入理解这个还需要专门去学习一下相关知识。
再回到整个模型的工作过程,前面说过了encoder,encoder得到的![]() 是z的一个分布,每一个z_ij都是只在K种edge type中取值的,因此得到分布之后按照分布采样得到z_ij。直接采样是不可取的,因为latent variable是离散的,不能使用reparametrization trick来进行反向传播。一个最近很受欢迎的解决这个问题的办法是先为这个离散的分布搞一个连续的近似,然后在这个连续的分布上取值,然后使用repramatrization trick来从这个近似中获得(biased)gradients(其实这里一直没看懂)。sample是按照一个叫做concrete distribution来选取的:
是z的一个分布,每一个z_ij都是只在K种edge type中取值的,因此得到分布之后按照分布采样得到z_ij。直接采样是不可取的,因为latent variable是离散的,不能使用reparametrization trick来进行反向传播。一个最近很受欢迎的解决这个问题的办法是先为这个离散的分布搞一个连续的近似,然后在这个连续的分布上取值,然后使用repramatrization trick来从这个近似中获得(biased)gradients(其实这里一直没看懂)。sample是按照一个叫做concrete distribution来选取的:![]() 。
。![]() ,是和Gumbel(0,1)独立同分布的,τ是一个控制采样光滑度(smoothness)的参数,当τ趋于0的时候,这个分布会从每一类的分布收敛到one-hot samples,我猜应该是说本来每一个类别可能都有相当数值的概率分布,收敛到one-hot就是只有一个类别有数值为1的概率密度,其他位置都是0。但是这里提到的reprarametrization trick说的是啥并没有理解,在网上查reprarametrization是将参数方程的参数进行更换,但是这里说是用来反向传播的,就没有很理解。
,是和Gumbel(0,1)独立同分布的,τ是一个控制采样光滑度(smoothness)的参数,当τ趋于0的时候,这个分布会从每一类的分布收敛到one-hot samples,我猜应该是说本来每一个类别可能都有相当数值的概率分布,收敛到one-hot就是只有一个类别有数值为1的概率密度,其他位置都是0。但是这里提到的reprarametrization trick说的是啥并没有理解,在网上查reprarametrization是将参数方程的参数进行更换,但是这里说是用来反向传播的,就没有很理解。
整个训练过程是这样的:得到一个训练样本x,首先通过encoder计算分布,然后从分布的concrete reparameterizable approximation(按照之前的描述,这个应该是用连续的分布近似之后进行了重新参数化reparameterization),然后运行decoder计算![]() ,ELBO目标包括reconstruction error
,ELBO目标包括reconstruction error![]() =
= (就是预测的和实际的观察值的差值,所以其实这也是有监督学习?),和KL divergence,这个是熵的相加
(就是预测的和实际的观察值的差值,所以其实这也是有监督学习?),和KL divergence,这个是熵的相加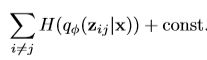 最后作者还说,由于使用了reparameterizable approximation,因此可以通过反向传播计算梯度并且优化。
最后作者还说,由于使用了reparameterizable approximation,因此可以通过反向传播计算梯度并且优化。
本文技术部分的结构是总分,先是介绍了整体的网络框架,然后介绍各个局部操作,包括encoder、decoder等等。