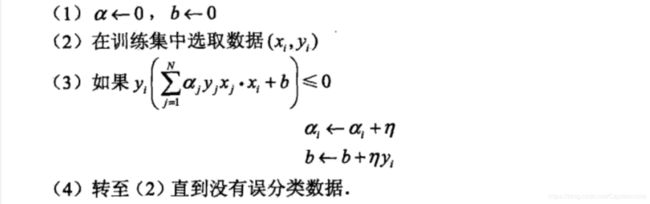统计学习方法笔记

统计学习方法笔记

CHAP 1 : 统计学习方法概论

1.1 统计学习简述

方法分类：监督学习，非监督学习，半监督学习，强化学习，本书主要讨论监督学习

统计学习方法三要素：模型（假设空间），策略（评价准则），算法（模型学习算法）

主要步骤（基于三要素）：获取到数据->确定假设空间->确定模型选择准则->实现最优模型算法->利用模型进行分析与预测

1.2 监督学习

定义：学习一个模型，对于任意一个输入，都有一个好的输出作为预测

掌握简单术语：输入空间（特征空间）输出空间，样本（输入输出对），假设空间( P(Y|X) 或 Y=f(x) )

​ 联合概率分布（输入输出随机变量X,Y遵循联合概率分布P(X,Y)

问题的形式化：由N个样本点，学习系统训练出模型后作为预测系统，预测系统对于给定的测试样本集中输入的X(N+1),由模型给出Y(N+1):
$$Y_{N+1}=argma{x}_{Y_{N+1}}P(Y_{N+1}|X_{N+1})$$
或
$$Y_{N+1}=f(X_{N+1})$$

1.3 统计学习三要素

模型对应的是假设空间，参数空间；算法归结到最后就是一个最优化问题，这个最优化问题的目标函数就是策略中的评价准则，引入损失函数和风险函数的概念：

损失函数：预测值与真实值之间的度量预测错误的程度，包括：0-1损失函数，平方损失函数，绝对损失函数，对数损失函数；损失值越小，模型越好。，记作
$$L(f(X),Y)$$
风险函数：由于损失函数的输入输出均为符合联合分布的随机变量，因此将损失函数的期望定义为风险函数,记作
$$R_{exp}(f)={\int }_{X\ast Y}L(f(x),y)\ast P(x,y)dxdy$$
但由于联合分布未知，因此由大数定律以以下的经验风险代替风险函数,N为训练集中样本数
$$R_{emp}(f)=\frac{1}{N}\sum _{i=1}^{N}L(f(x_i),y_i)$$
在训练数据，假设空间都确定后，算法最优化问题的的目标函数有以下两种选择

经验风险最小化 (ERM)
$$mi{n}_f\frac{1}{N}\sum _{i=1}^{N}L(f(x_i),y_i)$$
结构风险最小化（SRM)，添加正则化项，防止过拟合的出现
$$mi{n}_f\frac{1}{N}\sum _{i=1}^{N}L(f(x_i),y_i)+\lambda J(f)$$
J(f)为模型的复杂度，模型越复杂，J(f)越大。

1.4 模型的评估与选择

了解概念：测试误差，训练误差，过拟合

模型选择的经典方法：正则化，交叉验证（数据充足时，将数据划分为训练集，验证集，测试集，在学习不同复杂度的模型中，选择验证集上误差最小的；数据不充足时，简单交叉验证，S折交叉验证，留一交叉验证（N折交叉验证）

1.5 泛化能力

泛化误差：就是期望风险
$$R_{exp}(f)={\int }_{X\ast Y}L(f(x),y)\ast P(x,y)dxdy$$
接下来研究泛化误差的上界，它通常具有性质：样本容量增加时，泛化上界趋于0；假设空间容量增大，泛化上界增加，接下来引入能够说明该问题的泛化误差上界的定理

对于二分类问题，当假设空间是有限个函数的集合F={f1,f2…fd}时，对任意一个属于假设空间的函数f，至少以1-σ的概率使得以下不等式成立
$$R(f)\le R^{{}^{\prime }}(f)+\epsilon (d,N,\sigma )$$
其中
$$R^{{}^{\prime }}(f)=\frac{1}{N}\sum _{i=1}^{N}L(f(x_i),y_i)$$

$$R(f)={\int }_{X\ast Y}L(f(x),y)\ast P(x,y)dxdy=E(L(f(X),Y))$$

$$\epsilon (d,N,\sigma )=\sqrt{\frac{1}{2N}(logd+log\frac{1}{\sigma })}$$

证明过程较多，手写如下图：
先证明了markov不等式，Hoeffdinh引理->Hoeffding不等式，最后证明泛化误差上限定理。
证明思路来源：
Hoeffding inequality
Markov inequality
Hoeffding lemma

1.6 生成模型和判别模型

生成模型：数据学习+联合概率分布得到的模型P(Y|X)

判别模型：由数据直接学得P(Y|X)或Y=f(X)

Chap2 ：感知机

2.0 分类问题

定义：输出变量为有限个离散值的监督学习模型

评价分类器性能的指标：

real\predict	1	-1
1	TP	FP
-1	FP	TN

精确率：P=TP/(TP+FP) 预测为正类的正确率

召回率: R=TP/(TP+FN) 实际为正类中预测正确的个数

F1值：
$$\frac{2}{F_1}=\frac{1}{P}+\frac{1}{R}$$
P,R都很大的时候，F1也很大

2.1 感知机模型

2.1.1假设空间

由输入空间到输出空间的函数形式如下
$$f(x)=sign(w\ast x+b)$$
其中w,x为n维向量，b为实数

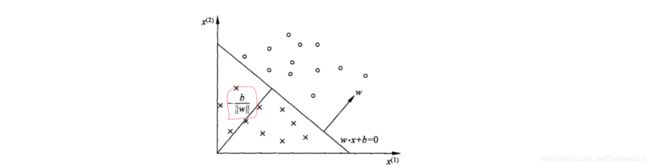
从几何意义上看，当wx+b>=0时，将x归为正类；当wx+b<0时，将x归为负类。对应到n维空间中，即找到一个超平面wx+b=0，将空间内的点按照其标记1，-1分为两部分，各在超平面的两侧。以二维为例大概是这个感觉

其中红线标志的为原点到直线的欧式距离，w为法向量。

2.1.2 评价准则

当损失函数选择误分类点的总数时，对于每一个分类点都要计算wx+b的符号后判断是1还是-1，这样显然关于w和b不是连续的，因此不能选择这样的损失函数。另一种选择方案是，见将损失函数的定义为所有分类错误点到超平面的距离和，如果所有点都分类正确则损失函数值为0，否则为正数，具体的损失函数如下：
$$minL(w,b)=-\sum _{x_{i}inM}{y}_i(w\ast x_i+b)$$
这里省略了除以w的范数，对于除以一个常数，去掉也没有什么影响

2.1.3 学习算法

采用随机梯度下降法解决目标函数L(w,b)的最小化问题，算法描述如下：

其中的η为0-1之间的学习率，学习率选的太小，收敛速度会很慢，选的太大又有可能导致发散，因此应多尝试几组学习率然后选择最优的。

除了以上的原始形式，还有如下的对偶形式，有上述算法可知，w为yixi的线性组合，b为yi的线性组合，因此先假设w和b具有上述线性组合的形式，然后用随机梯度下降法对系数进行调整，原理都是一样的。

算法如下：

该算法的优势在于，在计算xi*xj是不必进行实际计算，而是直接读取之前存储在Gram矩阵中的元素即可。

2.2 收敛性证明

这一部分的证明较简单，书上也写的比较详细

2.5 代码实现

#调用sklearn实现
#Perception of sklearn
import numpy as np
from sklearn.datasets import make_classification
from sklearn.linear_model import Perceptron
from matplotlib import pyplot as plt
from sklearn.model_selection import train_test_split,KFold
from sklearn.metrics import f1_score
#Generate data
X , y = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_repeated=0, n_classes=2)
X_positive = X[y==1]
X_negative = X[y==0]
Y_positive=y[y==1]
Y_negative=y[y==0]
f=[]
# 10 fold Cross Validation
for train_index,test_index in KFold(n_splits=10).split(X):
    #X_train,X_test,y_train,y_test=train_test_split(X[],y,test_size=0.3)
    X_train,y_train=X[train_index],y[train_index]
    X_test,y_test=X[test_index],y[test_index]
    P=Perceptron()
    P.fit(X_train,y_train)
    Pre=np.array(list(P.predict(X_test)))
    f.append(f1_score(y_test,Pre))
#Final result
train_index,test_index=list(KFold(n_splits=10).split(X))[f.index(max(f))]
X_train,y_train=X[train_index],y[train_index]
X_test,y_test=X[test_index],y[test_index]
P=Perceptron()
P.fit(X_train,y_train)
Pre=np.array(list(P.predict(X_test)))
plt.scatter(X_positive[:,0],X_positive[:,1],color="red")
plt.scatter(X_negative[:,0],X_negative[:,1],color="blue")
w=P.coef_
b=P.intercept_
st=np.min(X)
ed=np.max(X)
step=np.linspace(st,ed,50)
plt.plot(step,(-w[0][0]*step-b)/w[0][1],color="black")
plt.show()

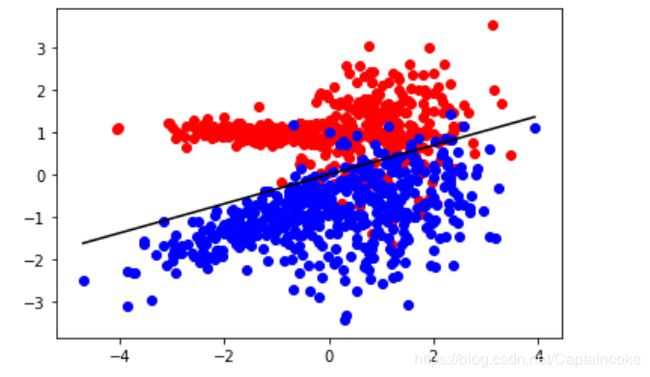
运行效果如下：

手动写算法总是跳不出循环，求大神帮忙看看哪里有问题

#手写算法实现
#Manual Perception
from sklearn.datasets import make_classification
from matplotlib import pyplot as plt
from sklearn.model_selection import train_test_split,KFold
from sklearn.metrics import f1_score
import numpy as np

class Perception:
    def __init__(self,x,y):
        self.tdx = np.array(x)
        self.tdy = np.array(y)
        self.w = np.zeros(2)
        self.b = 0

    def fit(self):
        n = 0
        #当存在分类错误的数据时，计算
        while np.sum(([np.dot(self.tdx[i-1:i:1][0],self.w) for i in np.arange(1,self.tdx.shape[0]+1)])*self.tdy<=0)>0:
            for xi,yi in zip(self.tdx,self.tdy):
                #当此数据计算错误时，更新
                if yi*(np.dot(xi,self.w)+self.b)<= 0:
                    self.w += yi*xi
                    self.b += yi
                    n += 1
                    print('w:',self.w,' b:',self.b,' 第%d次迭代'%n)
                #如果全部数据被分类正确
                if np.sum(([np.dot(self.tdx[i-1:i:1][0],self.w) for i in np.arange(1,self.tdx.shape[0]+1)])*self.tdy<=0.001)==0:
                    break
        return self.w,self.b
    def predict(self,x):
        return np.array([1 if i>0 else 0 for i in list(np.dot(x,self.w)+self.b)])

#Generate data
X , y = make_classification(n_samples=10,n_features=2, n_informative=2, n_redundant=0, n_repeated=0, n_classes=2)
X_positive = X[y==1]
X_negative = X[y==0]
Y_positive=y[y==1]
Y_negative=y[y==0]
f=[]
# 10 fold Cross Validation
for train_index,test_index in KFold(n_splits=10).split(X):
    X_train,y_train=X[train_index],y[train_index]
    X_test,y_test=X[test_index],y[test_index]
    y_train_adjust=[ 1 if i>0 else -1 for i in y_train]
    P=Perception(X_train,y_train_adjust)
    P.fit()
    Pre=np.array(list(P.predict(X_test)))
    f.append(f1_score(y_test,Pre))
#final result
print(f)
train_index,test_index=list(KFold(n_splits=10).split(X))[f.index(max(f))]
X_train,y_train=X[train_index],y[train_index]
X_test,y_test=X[test_index],y[test_index]
P=Perception(X_train,y_train)
P.fit()
Pre=np.array(list(P.predict(X_test)))
plt.scatter(X_positive[:,0],X_positive[:,1],color="red")
plt.scatter(X_negative[:,0],X_negative[:,1],color="blue")
w=P.w
b=P.b
st=np.min(X)
ed=np.max(X)
step=np.linspace(st,ed,50)
plt.plot(step,(-w[0]*step-b)/w[1],color="black")
plt.show()