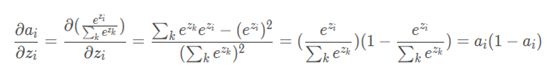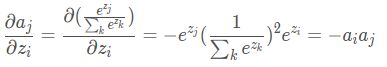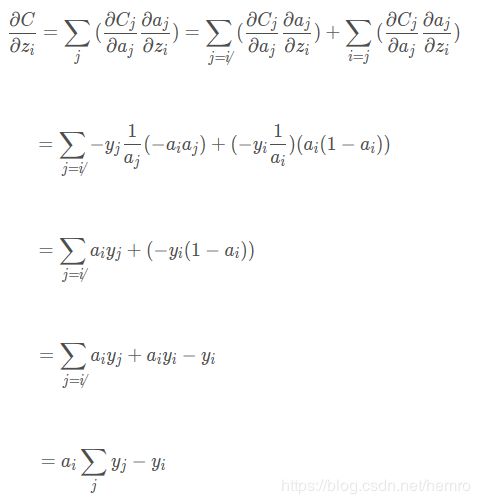深度学习之 softmax和交叉熵
记录 深度学习经典输出单元函数softmax和损失函数cross- entropy组合的推理过程
以识别0~9的手写例子来尝试描述这个问题,假设输入数据集为28x28的手写数字(单通道)。
那么输入图片X为28x28 = 784 维的一个向量。并,简单起见使用单层网络W_i x + b。
假设
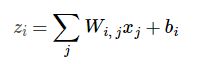
等式右边:
输入图片X像素0~784 * Wij + bi
其中Wij 是i数字对0j(0784)像素的权值
等式左边:
输出值,z_i对应数字i(i为0到9)的计算结果。
假设一张“1”的手写图片计算结果z_1一个很高的值,其他z_i(0,2,…9)很小的值,完美,我们可以预测它为1。
实际上初始计算结果是完全随机的值,我们的目标就是优化这些权值,能够每张数字i的图片上输出值很大,
i以外的数字图片上输出值很小。(这里大和小只是一个概念,主要目的是计算结果要有差异,在对应数字的结果
表现和非对应数字结果表现有差异,这样我们好预测,当然这个差异越明显越好)
1 softmax函数
Softmax归一化指数函数,主要是把上述输出结果概率化:
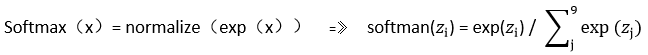
其中z_i是是神经网络第i个输出
如:
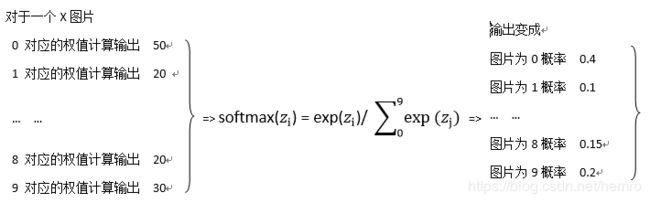
这样完全能以softmax(z_i)来表示数字i的概率了,上面提过要输出有差异,但这个差异怎么定义呢,
不好说。概率化就好办了,最大概率不为1,最小为0。那就对应标量的概率往1方向优化,非对应的往0方向优化就好。
Softmax:
1)从上面可以看到softmax使输出结果概率化,和多分类问题天然吻合,优化就使把概率往实际标签方向优化即可。
2)使用exp,因为优化过程通常会求偏导,exp求导方便。另外每个分类器输出经过exp,作为指数函数使得结果
差异扩大,加速分类。
3)和代价函数cross-entropy一起使用使得网络优化变得更简单。
2 交叉熵
损失函数,也叫代价函数,我们模型的优化尽可能使这个损失减少。比如均方差,在目标数据集上模型输出和
实际结果的均方差尽可能小,来衡量一个模型的好坏。而我们这里讨论的是另一个非常漂亮的代价函数 - 交叉熵。
1、定义
先看看它长什么样:
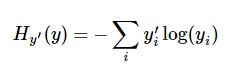
y 是我们预测的概率分布, y’ 是实际的分布。简单理解是,交叉熵是用来衡量我们的预测用于描述真相的低效性。
下面看交叉熵的来龙去脉
1)自信息
I(x) = - log( p(x) ) 以1/e(这里log指e为底)的概率观测到一个事件时获得的信息量。
2)香浓熵
整个概率分布中的不确定性总量进行量化。
![]()
即
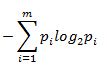
表示混杂程度,香浓熵越高混杂程度越高(比如,一个罐子里两种硬币,其中一种硬币占绝大多数,
这个叫纯度高,即混杂度低,香浓熵低),显然上面的例子,对于一个数字判断香浓熵越低越好,
纯度越高,判断准确率越高.
3)散度(KL)
两个分布的差异
![]()
即
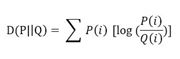
在概率论或信息论中,KL散度( Kullback–Leibler divergence),又称相对熵(relative entropy),
是描述两个概率分布P和Q差异的一种方法。它是非对称的,这意味着D(P||Q) ≠ D(Q||P)。特别的,在信息
论中,D(P||Q)表示当用概率分布Q来拟合真实分布P时,产生的信息损耗,其中P表示真实分布,Q表示P
的拟合分布。
4)交叉熵
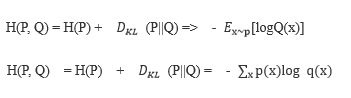
和散度比少左边的一项H(P),针对Q最小化交叉熵等价于最小化KL散度,因为Q并不参与被省略的那一项H(P)。
实际应用中P是以知道的结果(数据分布),Q为计算得到概率值(模型分布),目标就是这两个概率尽量一样,一个
是真实概率,另一个是优化的概率,使优化的概率往真实分布方向优化,或者说使这个交叉熵变小。
2、 代价函数求导推理
回到我们正题,损失函数 - 交叉熵:
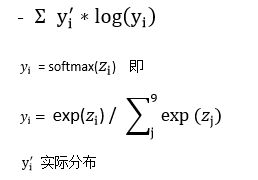
为了保持其他推理看起来一致,重新定义下上述公式:

接下来看推理过程
手工输入公式实在费劲,这里参考博文中的公式
https://blog.csdn.net/qian99/article/details/78046329
我们优化最终参数W和b进行优化,损失函数loss进行求对w和b梯度。首先我们神经网络输出z_i对loss的梯度。
![]()
由复合函数求偏导数法则:

首先看a_j对C偏导
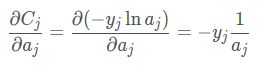
再z_i对a_j偏导,这里分i=j和 i≠j两种情况,因为复合函数求导链式法则,z_i对所有中间函数a_j求导。
其中yi只有i=j时1,其他情况都为0,那么
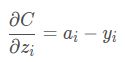
这个结果看起来非常简洁,看到softmax和cross-entropy的完美结合。z_i为神经网络第i输出,得到
![]()
后,继续w、b(或前一层的神经输入)再z_i求导就即可