奇异值分解---SVD(待补充)
什么是奇异值分解?
奇异值分解是指将一个非零的 m * n 实矩阵A, 表示为以下三个实矩阵乘积形式的运算,即进行矩阵的因子分解。
A = U Σ V T A = U\Sigma V^T A=UΣVT
U U U 是 m 阶正交矩阵,V 是 n 阶正交矩阵, Σ = d i a g ( σ 1 , σ 2 , . . . , σ p ) \Sigma = diag(\sigma_1,\sigma_2,..., \sigma_p) Σ=diag(σ1,σ2,...,σp) 是由降序排列的非负的对角线元素组成的 m * n 矩阵对角矩阵。 σ \sigma σ 称为矩阵的奇异值, U U U 的列向量称为左奇异向量, V V V 的列向量称为右奇异向量。
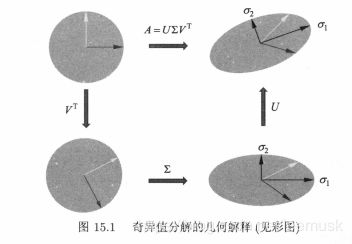
从几何角度上理解,基于 A = U Σ V T A = U\Sigma V^T A=UΣVT 的线性变换,等价于经过坐标系的旋转或反射变换 V T V^T VT ,坐标轴的缩放变换 Σ \Sigma Σ ,以及坐标系的旋转或反射变换 U, 得到向量 A x ∈ R m Ax \in R^m Ax∈Rm.
奇异值分解的特性
- 给定一个任意的实矩阵,奇异值分解一定存在。
- 矩阵奇异值分解是不唯一的。
紧奇异值分解和截断奇异值分解
紧奇异值分解:
设有 m * n 实矩阵 A ,其秩为 rank(A) = r, r <= min(m, n),则称 U r Σ r V r T U_r \Sigma_r V_r^T UrΣrVrT 为A 的紧奇异值分解,即
A = U r Σ r V r T A = U_r \Sigma_r V_r^T A=UrΣrVrT
截断奇异值分解:
在矩阵的奇异值分解中,只取最大的K个奇异值(K < r)对应的部分,就得到矩阵的截断奇异值分解。实际应用中得到的奇异值分解师,通常指截断奇异值分解。
设有 m * n 实矩阵 A ,其秩为 rank(A) = r, 0 < k < r 0 < k < r 0<k<r,则称 U k Σ k V k T U_k \Sigma_k V_k^T UkΣkVkT 为A 的紧奇异值分解,即
A ≃ U k Σ k V k T A \simeq U_k \Sigma_kV_k^T A≃UkΣkVkT
如何进行奇异值分解
主要思想:矩阵 A 的奇异值分解可以通过求对称矩阵 A T A A^TA ATA 的特征值和特征向量得到。 A T A A^TA ATA 的特征向量构成正交矩阵 V V V 的列; A T A A^TA ATA 的特征值 λ j \lambda_j λj 的平方根为奇异值 σ i \sigma_i σi, 即
σ j = λ j , j = 1 , 2 , . . . , n \sigma_j = \sqrt{\lambda_j}, \quad j= 1,2, ..., n σj=λj,j=1,2,...,n
计算过程主要分为4个阶段:
(1). 求 A T A A^TA ATA 的特征值和特征向量
(2). 求 n 阶正交矩阵 V
(3). 求 m * n 对角矩阵 Σ \Sigma Σ
(4). 求 m 阶正交矩阵 U
(5). 得到奇异值分解
需要注意的是第四阶段,计算过程如下:
首先需要由 A = U Σ V T A = U\Sigma V^T A=UΣVT 易知
A V = U Σ AV = U\Sigma AV=UΣ
比较这一等式两端的第 j 列,得到
A v j = σ j u j , j = 1 , 2 , . . , n Av_j = \sigma_ju_j, \quad j = 1,2, .., n Avj=σjuj,j=1,2,..,n
对A 的前 r 个正奇异值,令
u j = 1 σ j A v j , j = 1 , 2 , . . , n u_j = \frac 1 { \sigma_j} Av_j , \quad j = 1,2, .., n uj=σj1Avj,j=1,2,..,n
得到 U 1 = [ u 1 , u 2 , . . . , u r ] U_1 = [ u_1, u_2, ..., u_r ] U1=[u1,u2,...,ur]
求 A T A^T AT 的两空间的一组标准正交基,令
U 2 = [ u r + 1 , u r + 1 , . . . , u m ] U_2 = [u_{r+1}, u_{r+1}, ..., u_m] U2=[ur+1,ur+1,...,um]
并令
U = [ U 1 . U 2 ] U = [U_1. U_2] U=[U1.U2]
我们需要知道的是在实际的使用过程中,我们关注的是 A T A A^TA ATA 的特征值,而无需计算 A T A A^TA ATA.
简单理解,有待补充。。。