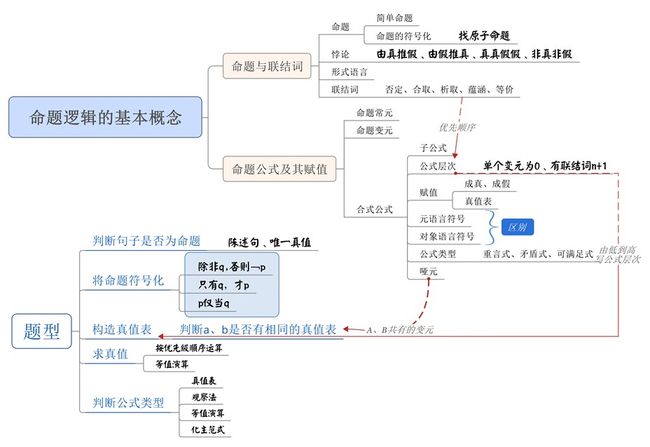
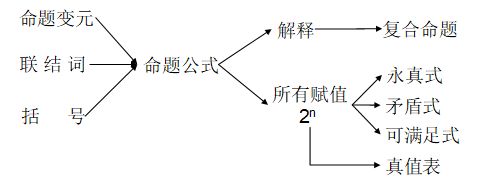
离散数学-1 命题逻辑的基本概念
定义1.1 设 p为命题,复合命题"非p"(或"p的否定")称为p的否定式,记作Øp,符号Ø称作否定联结词. 规定Øp 为真当且仅当p为假.
定义1.2 设p,q为两个命题,复合命题"p并且q"(或"p与 q")称为p与q的合取式,记作p∧q,∧称作合取联结词. 规定p∧q为真当且仅当p与q同时为真.
定义1.3 设p, q为两个命题,复合命题"p或q"称作p与q的析取式,记作p∨q,∨称作析取联结词. 规定p∨q为假当且仅当p与q同时为假.
定义1.4 设p, q为两个命题,复合命题"如果p, 则q"称作p与q的蕴涵式,记作pq,并称p是蕴涵式的前件,q为蕴涵式的后件,®称作蕴涵联结词. 规定:pq为假当且仅当p为真q为假.pq 的逻辑关系:q为 p 的必要条件
定义1.5 设 p, q为两个命题,复合命题"p当且仅当q"称作p与q的等价式,记作pq,«称作等价联结词. 规定pq为真当且仅当p与q同时为真或同时为假.pq 的逻辑关系:p与q互为充分必要条件
定义1.6 合式公式(简称公式)的递归定义:
(1) 单个命题变项和命题常项是合式公式, 称作原子命题公式
(2) 若A是合式公式,则 (A)也是
(3) 若A, B是合式公式,则(AB), (AB), (AB), (AB)也是
(4) 只有有限次地应用(1)—(3) 形成的符号串是合式公式
定义1.7
(1) 若公式A是单个命题变项,则称A为0层公式.
(2) 称 A 是 n+1(n≥0) 层公式是指下面情况之一:
(a) A=B, B 是 n 层公式;
(b) A=BC, 其中B,C 分别为 i 层和 j 层公式,且 n=max(i,j);
(c) A=BC, 其中 B,C 的层次及 n 同(b);
(d) A=BC, 其中B,C 的层次及 n 同(b);
(e) A=BC, 其中B,C 的层次及 n 同(b).
(3) 若公式A的层次为k, 则称A为k层公式.
定义1.8设p1, p2, … , pn是出现在公式A中的全部命题变项, 给p1, p2, … , pn各指定一个真值, 称为对A的一个赋值或解释. 若使A为1, 则称这组值为A的成真赋值; 若使A为0, 则称这组值为A的成假赋值.
定义1.9将命题公式A在所有赋值下取值的情况列成表, 称作
A的真值表.
构造真值表的步骤:
(1) 找出公式中所含的全部命题变项p1, p2, … , pn(若无下角标则按字母顺序排列), 列出2n个全部赋值, 从000开始, 按二进制加法, 每次加1, 直至111为止.
(2) 按从低到高的顺序写出公式的各个层次.
(3) 对每个赋值依次计算各层次的真值, 直到最后计算出公式的真值为止.
定义1.10
(1) 若A在它的任何赋值下均为真, 则称A为重言式或永真式;
(2) 若A在它的任何赋值下均为假, 则称A为矛盾式或永假式;
(3) 若A不是矛盾式, 则称A是可满足式.
题型
1、命题符号化
2、求复合命题的真值与命题公式的真值
3、判断公式类型