通过机器学习,对泰坦尼克号乘客的最终生存概率进行预测
这是kaggle上的一个开源项目。train集中,记载了泰坦尼克号乘客的各类信息,包括姓名、年龄、性别、船舱、家庭状况等,以及最终的生存状况(0表示死亡,1表示存活),通过清洗、探索分析train,建立合适的模型,对test集中的客户的生存状况进行预测。train集中,embarked代表上岸港口,pclass代表社会阶层,cabin代表船舱代号,sex代表性别,其他略。
# 一、引入基础包、数据
-*- coding:utf-8 –*-
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
pd.set_option("display.max_columns", None)
warnings.filterwarnings("ignore")
train = pd.read_csv("F:/data/train.csv")
test = pd.read_csv("F:/data/test.csv")
#查看train集的基本信息
print train.shape
![]()
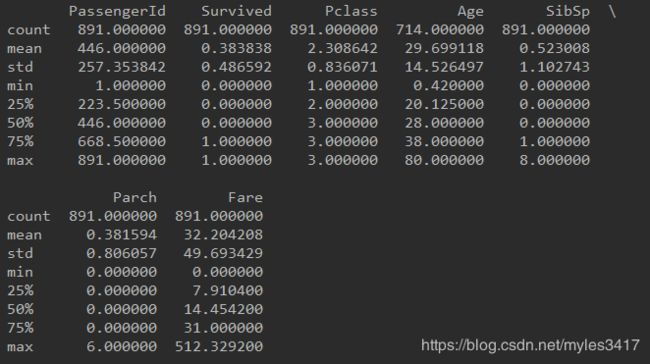
print train.describe()
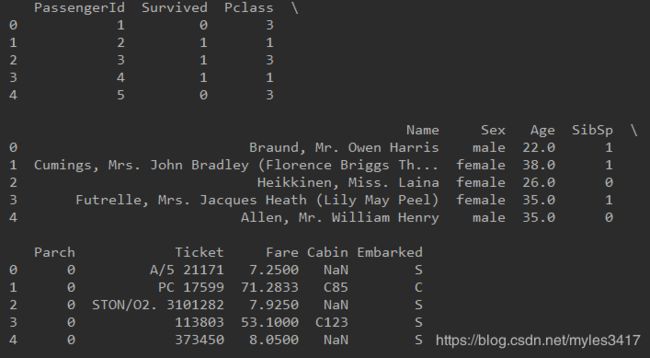
print train.head(10)
#查看test集的基本信息
print test.shape
![]()
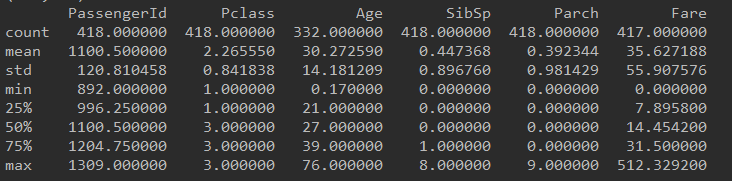
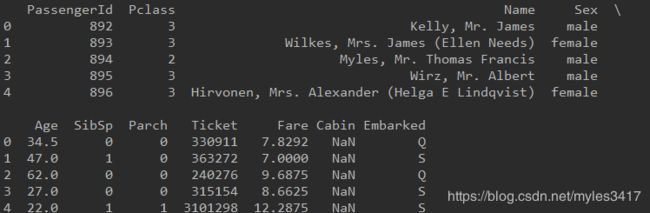
print test.describe()
**# 二、清洗数据**
trainPassID = train["PassengerId"]
testPassID = test["PassengerId"]
**# 处理train中Embarked的空值**
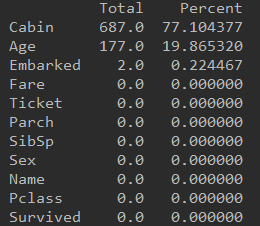
traintotal = train.isnull().sum().sort_values(ascending=False).astype(float)
trainpercent = train.isnull().sum().sort_values(ascending=False)/len(train)*100
traintp = pd.concat([traintotal,trainpercent],axis=1,keys=["Total","Percent"])
print(traintp)
#train集中空值数量比例如下
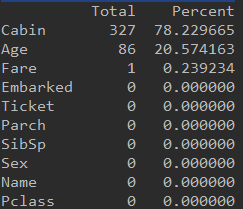
testtotal = test.isnull().sum().sort_values(ascending = False)
testpercent = test.isnull().sum().sort_values(ascending = False)/len(test)*100
testtp = pd.concat([testtotal, testpercent], axis = 1,keys= ["Total", "Percent"])
print (testtp)
#test集中空值数量比例如下
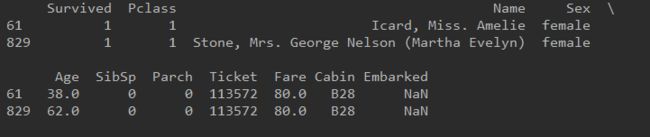
print (train[train["Embarked"].isnull()])
#train集中Embarked列空值具体信息如下
sur = train['Survived']
train = train.drop(['Survived'],axis=1)
alldata = pd.concat([train,test],ignore_index=False)
alldata['Cabin'] = alldata['Cabin'].fillna('N')
alldata['Cabin'] = [i[0] for i in alldata['Cabin']]
missing = alldata[alldata['Cabin'] == 'N']
notmissing = alldata[alldata['Cabin'] != 'N']
print alldata.groupby('Cabin')['Fare'].mean().sort_values
A 41.244314
B 122.383078
C 107.926598
D 53.007339
E 54.564634
F 18.079367
G 14.205000
N 19.132707
T 35.500000
查看train与test数据文件中,各船舱对应的费用均值,依靠费用均值,来推测乘客所在船舱
def cabin_filler(i):
a = 0
if i<16:
a = "G"
elif i>=16 and i<27:
a = "F"
elif i>=27 and i<38:
a = "T"
elif i>=38 and i<47:
a = "A"
elif i>= 47 and i<53:
a = "E"
elif i>= 53 and i<54:
a = "D"
elif i>=54 and i<116:
a = 'C'
else:
a = "B"
return a
missing['Cabin'] = missing['Fare'].apply(lambda x: cabin_filler(x))
alldata = pd.concat([missing,notmissing],axis=0)
alldata = alldata.sort_values(by='PassengerId')
train = alldata[:891]
test = alldata[891:]
train['Survived'] = sur
编写函数推测船舱编号,至此已完成船舱数据填充。
fig, ax = plt.subplots(figsize=(16,12),ncols=2)
ax1 = sns.boxplot(x="Embarked", y="Fare", hue="Pclass", data=train, ax = ax[0]);
ax2 = sns.boxplot(x="Embarked", y="Fare", hue="Pclass", data=test, ax = ax[1]);
ax1.set_title("Training Set", fontsize = 18)
ax2.set_title('Test Set', fontsize = 18)
plt.show()
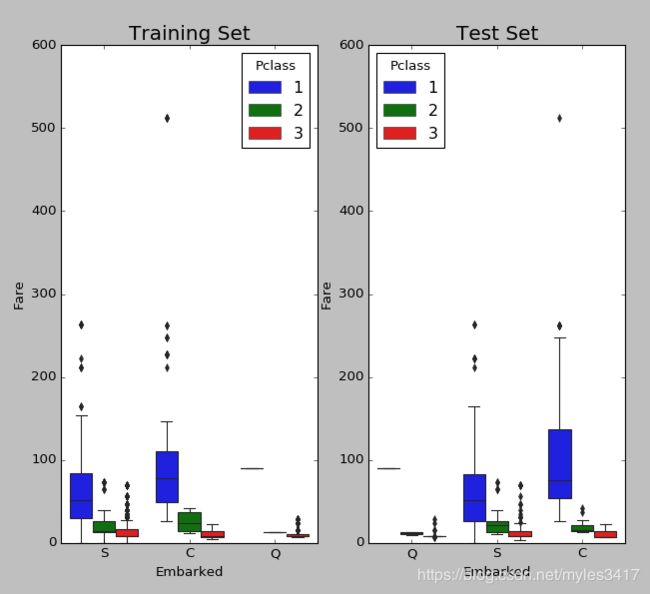
可以看到,同样是80fare,pclass为1的人群,大多在C口上岸,故将Embarked空值填充为C
train["Embarked"] = train["Embarked"].fillna("C")
test中的fare列有少数空值,根据其他有相似特征的行的fare均值补充
test[test['Fare'].isnull()]
missing_value = test[test["Pclass"] == 3][test["Embarked"] == "S"][test["Sex"] == "male"]["Fare"].mean()
test['Fare'] = test["Fare"].fillna(missing_value)
三、因子分析与可视图
# sex分布可视图
sns.set(style="darkgrid")
pal = {1:"seagreen", 0:"gray"}
sns.set(style="darkgrid")
plt.subplots(figsize = (15,8))
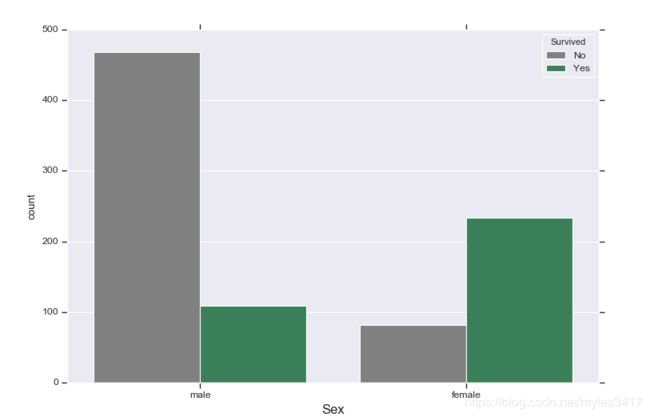
ax = sns.countplot(x = "Sex", hue="Survived",data = train,linewidth=1, palette = pal)
plt.xlabel("Sex", fontsize = 15)
leg = ax.get_legend()
leg.set_title("Survived")
legs = leg.texts
legs[0].set_text("No")
legs[1].set_text("Yes")
plt.show()
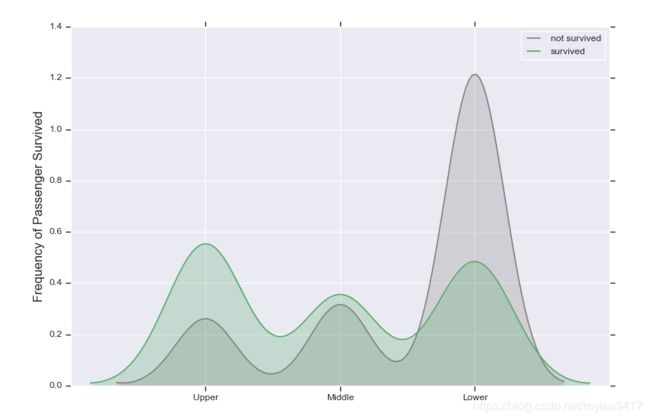
# pclass分布
fig = plt.figure(figsize=(15,8),)
ax = sns.kdeplot(train["Pclass"][train["Survived"] == 0],color="gray",shade=True,label="not survived")
ax = sns.kdeplot(train["Pclass"][train["Survived"] == 1],color="g",shade=True,label="survived")
labels = ['Upper', 'Middle', 'Lower']
plt.xticks((1,2,3), labels)
plt.show()
fig = plt.figure(figsize=(15,8),)
ax=sns.kdeplot(train.loc[(train["Survived"] == 0),"Fare"] , color='gray',shade=True,label='not survived')
ax=sns.kdeplot(train.loc[(train["Survived"] == 1),"Fare"] , color='g',shade=True, label='survived')
plt.xlabel("Fare", fontsize = 15)
plt.show()
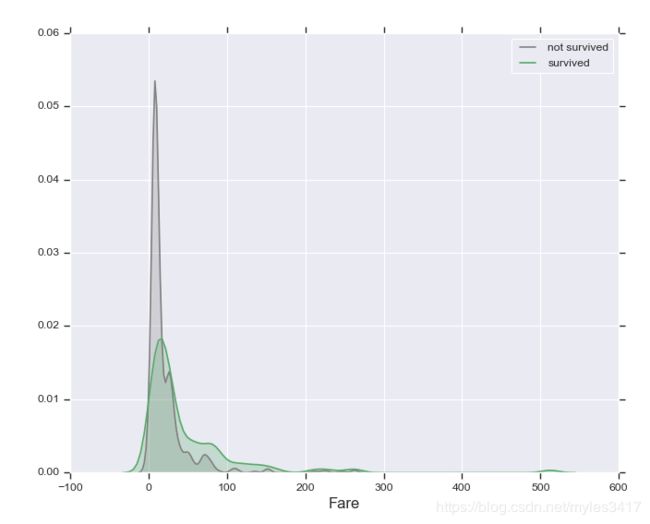
图表显示100美元以下的乘客生存概率低,同时有几个超过400美元的离群点
print train[train['Fare']>400]
PassengerId Pclass Name Sex Age \
258 259 1 Ward, Miss. Anna female 35.0
679 680 1 Cardeza, Mr. Thomas Drake Martinez male 36.0
737 738 1 Lesurer, Mr. Gustave J male 35.0
SibSp Parch Ticket Fare Cabin Embarked Survived
258 0 0 PC 17755 512.3292 B C 1
679 0 1 PC 17755 512.3292 B C 1
737 0 0 PC 17755 512.3292 B C 1
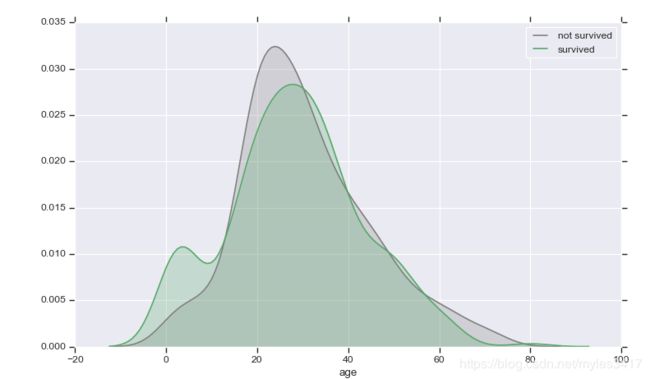
# age分布图
fig = plt.figure(figsize=(15,8),)
ax=sns.kdeplot(train.loc[(train['Survived'] == 0),'Age'] , color='gray',shade=True,label='not survived')
ax=sns.kdeplot(train.loc[(train['Survived'] == 1),'Age'] , color='g',shade=True, label='survived')
plt.xlabel('age')
plt.show()
# fare、sex、age分布图
pal = {1:"seagreen", 0:"gray"}
g = sns.FacetGrid(train, size=5,hue="Survived", col ="Sex", margin_titles=True,palette=pal,)
g.map(plt.scatter, "Fare", "Age",edgecolor="w").add_legend()
plt.show()
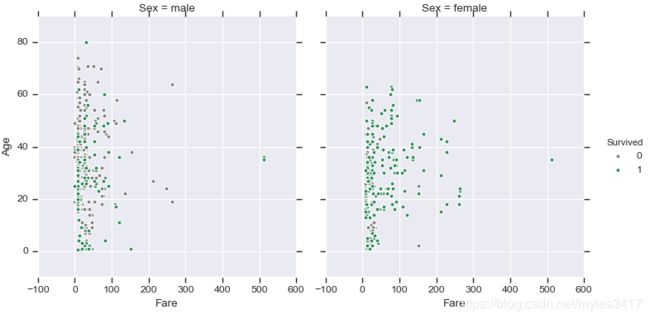
# 根据图表可知:1、女性存活率比男性高
# 2、上层阶级存活率最高,其次是中层阶级,其次下层
# 3、费用100以下的占大多数,但存活率低,200以上的存活率高,有3个512费用的离群点
# 4、0-15岁左右的存活率高,其他年龄无明显特点
# 四、统计概览
train['Sex'] = train.Sex.apply(lambda x: 0 if x == "female" else 1)
test['Sex'] = test.Sex.apply(lambda x: 0 if x == "female" else 1)
将sex文本数据替换为数值,female为0,male为1
print(train[['Pclass', 'Survived']].groupby("Pclass").mean())
Survived
Pclass
1 0.629630
2 0.472826
3 0.242363
for i in ["Survived","Sex","Pclass"]:
print(train.groupby(i).mean())
PassengerId Pclass Sex Age SibSp Parch \
Survived
0 447.016393 2.531876 0.852459 30.626179 0.553734 0.329690
1 444.368421 1.950292 0.318713 28.343690 0.473684 0.464912
Fare
Survived
0 22.117887
1 48.395408
PassengerId Pclass Age SibSp Parch Fare Survived
Sex
0 431.028662 2.159236 27.915709 0.694268 0.649682 44.479818 0.742038
1 454.147314 2.389948 30.726645 0.429809 0.235702 25.523893 0.188908
PassengerId Sex Age SibSp Parch Fare \
Pclass
1 461.597222 0.564815 38.233441 0.416667 0.356481 84.154687
2 445.956522 0.586957 29.877630 0.402174 0.380435 20.662183
3 439.154786 0.706721 25.140620 0.615071 0.393075 13.675550
Survived
Pclass
1 0.629630
2 0.472826
3 0.242363
rint(pd.DataFrame(abs(train.corr()["Survived"]).sort_values()))
Survived
PassengerId 0.005007
SibSp 0.035322
Age 0.077221
Parch 0.081629
Fare 0.257307
Pclass 0.338481
Sex 0.543351
Survived 1.000000
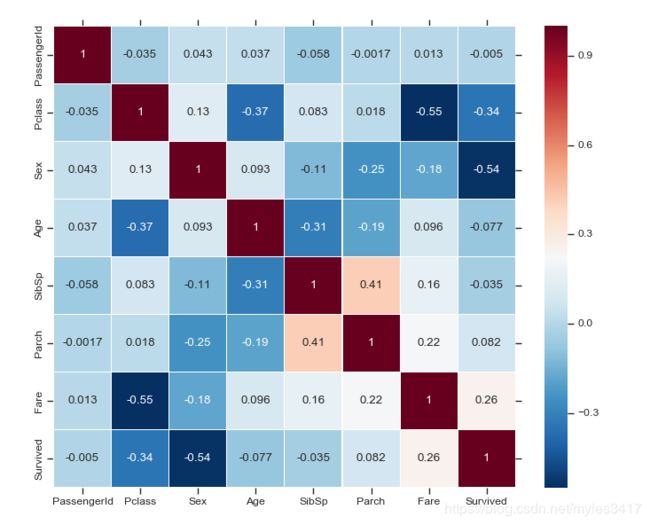
plt.subplots(figsize = (15,12))
sns.heatmap(train.corr(),annot=True,cmap = 'RdBu_r',linewidths=0.1,linecolor='white',vmax = 1,square=True)
plt.show()
# 使用t检验,验证sex与生存是否存在明显关联。H0:sex与生存间没有明显关联,H1:有明显关联
import scipy.stats as sts
import random
male = train[train['Sex'] == 1]
female = train[train['Sex'] == 0]
male_sample = random.sample(list(male['Survived']),50)
female_sample = random.sample(list(female['Survived']),50)
print (sts.ttest_ind(male_sample, female_sample))
Ttest_indResult(statistic=-6.819712206264365, pvalue=7.550631455261786e-10)
# p值小于显著性水平0.05,H1成立,sex与生存存在明显关系
# 五、特征处理
train = pd.get_dummies(train, columns=['Pclass','Cabin','Embarked','SibSp'],drop_first=False)
train = train.drop(['Name','Ticket'],axis=1)
test = pd.get_dummies(test, columns=['Pclass','Cabin','Embarked','SibSp'],drop_first=False)
test = test.drop(['Name','Ticket'],axis=1)
将所有文本特征经过OneHotEncoder转化
# 使用随机森林预测age中的空值,把age中的空值填上
train = pd.concat([train[[ "Age", "Sex"]], train.loc[:,"Fare":]], axis=1)
test = pd.concat([test[["Age", "Sex"]], test.loc[:,"Fare":]], axis=1)
from sklearn.ensemble import RandomForestRegressor
def filling_age(df):
age_df = df.loc[:, "Age":]
temp_train = age_df.loc[age_df.Age.notnull()]
temp_test = age_df.loc[age_df.Age.isnull()]
y = temp_train.Age.values
x = temp_train.loc[:, "Sex":].values
rfr = RandomForestRegressor(n_estimators=1500, n_jobs=-1)
rfr.fit(x, y)
predicted_age = rfr.predict(temp_test.loc[:, "Sex":])
df.loc[df.Age.isnull(), "Age"] = predicted_age
return df
filling_age(train)
filling_age(test)
x = train.drop(['Survived'], axis=1)
y = train["Survived"]
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x,y,test_size = .33, random_state = 0)
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
x_train = sc.fit_transform(x_train)
x_test = sc.transform(x_test)
test = sc.transform(test)
将train数据分为训练集与测试集两部分,并将其进行标准化处理。test文件进行同样操作。
# 六、建模
from sklearn.metrics import mean_absolute_error, accuracy_score,recall_score,f1_score
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import AdaBoostClassifier
models = []
models.append(('LogisticRegression',LogisticRegression()))
models.append(('KNN',KNeighborsClassifier()))
models.append(('GaussianNB',GaussianNB()))
models.append(('SVC',SVC(kernel = 'rbf', probability=True, random_state = 1, C = 3)))
models.append(('DecisionTree',DecisionTreeClassifier()))
models.append(('RandomForestClassifier',RandomForestClassifier(n_estimators=100,max_depth=9,min_samples_split=6, min_samples_leaf=4)))
models.append(('AdaBoostClassifier',AdaBoostClassifier()))
for mod_name, mod in models:
mod.fit(x_train,y_train)
xy_lst=[(x_train,y_train),(x_test,y_test)]
for i in range(len(xy_lst)):
x_part = xy_lst[i][0]
y_part = xy_lst[i][1]
y_pred =mod.predict(x_part)
if i ==0:
a = 'train'
else:
a = 'test'
print(a)
print(mod_name, '-ACC',round(accuracy_score(y_part,y_pred),3))
print(mod_name, '-REC', round(recall_score(y_part, y_pred),3))
print(mod_name, '-F1', round(f1_score(y_part, y_pred),3))
train
('LogisticRegression', '-ACC', 0.834)
('LogisticRegression', '-REC', 0.753)
('LogisticRegression', '-F1', 0.779)
test
('LogisticRegression', '-ACC', 0.817)
('LogisticRegression', '-REC', 0.73)
('LogisticRegression', '-F1', 0.75)
train
('KNN', '-ACC', 0.837)
('KNN', '-REC', 0.723)
('KNN', '-F1', 0.775)
test
('KNN', '-ACC', 0.793)
('KNN', '-REC', 0.658)
('KNN', '-F1', 0.705)
train
('GaussianNB', '-ACC', 0.43)
('GaussianNB', '-REC', 0.996)
('GaussianNB', '-F1', 0.575)
test
('GaussianNB', '-ACC', 0.403)
('GaussianNB', '-REC', 0.964)
('GaussianNB', '-F1', 0.549)
train
('SVC', '-ACC', 0.866)
('SVC', '-REC', 0.797)
('SVC', '-F1', 0.821)
test
('SVC', '-ACC', 0.797)
('SVC', '-REC', 0.721)
('SVC', '-F1', 0.727)
train
('DecisionTree', '-ACC', 0.992)
('DecisionTree', '-REC', 0.978)
('DecisionTree', '-F1', 0.989)
test
('DecisionTree', '-ACC', 0.797)
('DecisionTree', '-REC', 0.712)
('DecisionTree', '-F1', 0.725)
train
('RandomForestClassifier', '-ACC', 0.867)
('RandomForestClassifier', '-REC', 0.736)
('RandomForestClassifier', '-F1', 0.811)
test
('RandomForestClassifier', '-ACC', 0.82)
('RandomForestClassifier', '-REC', 0.676)
('RandomForestClassifier', '-F1', 0.739)
train
('AdaBoostClassifier', '-ACC', 0.842)
('AdaBoostClassifier', '-REC', 0.775)
('AdaBoostClassifier', '-F1', 0.792)
test
('AdaBoostClassifier', '-ACC', 0.803)
('AdaBoostClassifier', '-REC', 0.748)
('AdaBoostClassifier', '-F1', 0.741)
综合判断随机森林的准确率相对较高,故使用随机森林预测test文件
# 八、利用test数据预测
rf = RandomForestClassifier(n_estimators=100,max_depth=9,min_samples_split=6, min_samples_leaf=4)
rfc = rf.fit(x_train,y_train)
test_pred = rfc.predict(test)
results = pd.DataFrame({"PassengerId": testPassID, "Survived":test_pred})
print results
results.to_csv("titanic_pred.csv",index=False)
PassengerId Survived
0 892 0
1 893 0
2 894 0
3 895 0
4 896 0
5 897 0
6 898 0
7 899 0
8 900 1
9 901 0
10 902 0
11 903 0
12 904 1
13 905 0
14 906 1
15 907 1
16 908 0
17 909 0
18 910 0
19 911 0
20 912 0
21 913 0
22 914 1
23 915 0
24 916 1
25 917 0
26 918 1
27 919 0
28 920 0
29 921 0
.. ... ...
388 1280 0
389 1281 0
390 1282 1
391 1283 1
392 1284 0
393 1285 0
394 1286 0
395 1287 1
396 1288 0
397 1289 1
398 1290 0
399 1291 0
400 1292 1
401 1293 0
402 1294 1
403 1295 0
404 1296 1
405 1297 0
406 1298 0
407 1299 1
408 1300 1
409 1301 0
410 1302 0
411 1303 1
412 1304 0
413 1305 0
414 1306 1
415 1307 0
416 1308 0
417 1309 0