数学基础(四):支持向量机SVM数学推导(硬间隔,软间隔,核函数)
数学基础系列博客是自己在学习了稀牛学院&网易云课堂联合举办的《人工智能数学基础》微专业后的课程笔记总结。怀着对授课讲师Jason博士无限的敬佩与感激之情,我在完整听了两遍课程之后,对这门进行了笔记整理。Jason博士用深入浅出的方式把数学知识真的是讲透彻了,我的笔记显然无法完整传达Jason博士的精彩授课内容,在此非常推荐每一个打算进入或了解AI的同学去学习这门课程!
一:机器学习中的两类问题
1.1 回归问题
1.2 分类问题
- 分类问题预测的是离散值
今天我们来整理学习一下支持向量机,这么多天都没有更新机器学习算法系列,就是因为一直在学习SVM,但是,感觉我还是没有领悟支持向量机这个经典算法的精髓。只能在此将自己的理解整理一下,供各位朋友参考。在学习过程中也参考了很多优秀的博客,其中寒小阳的博客对自己帮助最大,在此表示非常感谢!在这篇文章中,我们着重从数学的角度来理解学习SVM。希望能够对真正理解算法有帮助。
二:支持向量机简介
首先,我们要说强调以下两点内容,可能现在还不清楚,但是当你读完博文之后,自然就能够理解这两句话的意思了。
- 支持向量机是一类分类算法。
- 我们需要使用有标签的数据进行训练,所以说SVM是有监督学习算法。
三:线性分类器和最优线性分类器
我们来说一下线性分类器。什么是线性分类器?顾名思义,数学表达为线性方程的分类器,我们就称之为线性分类器。从数学上来讲,形如 w T x + b = 0 \mathbf{w^Tx}+b=0 wTx+b=0的平面被称为超平面,在一维空间中,超平面就是一个点;在二维空间中,超平面就是一条直线;在三维空间中,超平面是一个平面;在更高维空间中,由于无法直观展现出来,因此我们称之为超平面。
其实,我们前面的算法中学习过这种分类器,那就是逻辑回归算法。大家仔细回忆一下,或者回顾一下前面的博客文章 机器学习算法系列(二):逻辑回归,逻辑回归本质上是通过判断一个样本点在分类直线的哪一侧来判定样本的类别,所以说逻辑回归的分类器就是一个线性分类器。但是能够区分两个样本的分类器只有一个吗?大家可以观察下边这幅图,从图中可以看出,能够区分两类样本点的直线其实有很多,那么这些直线的分类效果都一样吗?哪一条直线的分类效果最好呢?这也就引出了SVM算法。
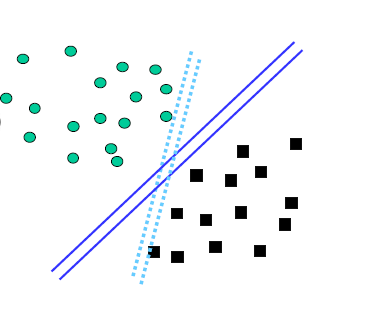
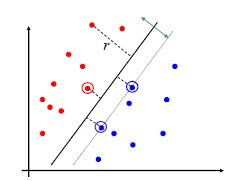
SVM算法本质上就是要找到一条直线(二维空间中为直线,高维空间中统称为超平面)将两类样本点尽可能地分开,使得直线离两类样本点的距离最大。这样的分类器鲁棒性最好。什么是鲁棒性?鲁棒性用土话说就是“皮实”,在预测的时候不容易出错,容错性更好。举个例子:
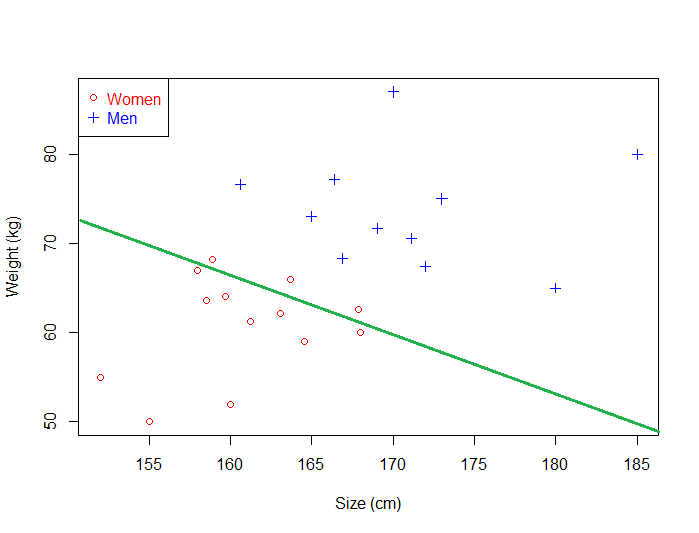
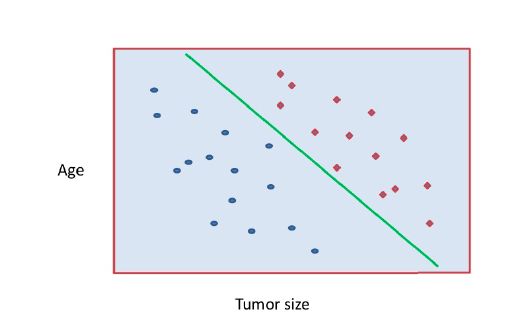
下图中有两类样本点(women和men),分别用“圆圈”和“十字”表示。我们仔细观察就会发现,图中的四条直线其实都可以把两类样本点分开,那么这四条直线都可取吗?
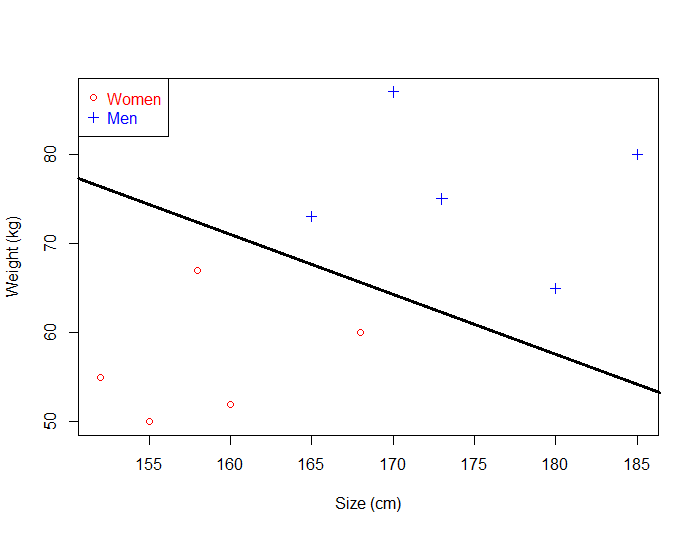
假如我们选取图中的绿色直线,然后用一些数据点来进行测试,如下图所示。很容易就会发现,红色样本点被分错了好多,这说明什么呢?说明这条直线的鲁棒性不好。很容易分类错误。究其原因,就是因为这条直线离红色样本点太近了。这种离某一个类别太近的分类器的分类效果就不是很好。那么,我们自然就能想到好的分类器应该满足的标准:离两类样本尽可能地远!
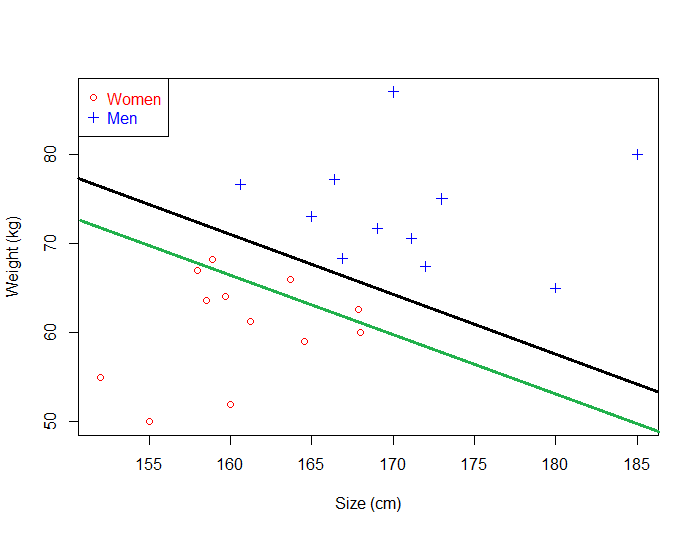
比如下图中的黑色分类器,离两类样本都比较远,当进行分类时,鲁棒性就很好,不容易分错。写到这里,我想读者朋友应该能够明白SVM的目标了吧。就是要找到一条离两类样本都尽可能远的直线!很容易可以理解,当分类器在两类样本正中间的时侯最合适。如果不在中间,那么肯定就偏向了某一类样本,因此,按照svm的目标,最优的线性分类器一定是在两类样本点的正中间。
四:SVM建模
4.1 点到超平面的距离
- 超平面 { x ∣ w T x + b = 0 } \{\mathbf{x}|\mathbf{w^Tx}+b=0\} {x∣wTx+b=0}
- 空间中任意一点p到该点的距离
r = ∣ w T p + b ∣ ∣ ∣ w ∣ ∣ 2 r = \frac{|\mathbf{w^Tp}+b|}{||\mathbf{w}||_2} r=∣∣w∣∣2∣wTp+b∣
推导:
4.2 SVM目标函数
-
几何间隔:(找出到超平面距离最小的那个点,然后计算出这个距离)
M = min i r i = min i ∣ w T x i + b ∣ ∥ w ∥ 2 M=\min _{i} r_{i}=\min _{i} \frac{\left|\mathbf{w}^{T} \mathbf{x}_{i}+b\right|}{\|\mathbf{w}\|_{2}} M=iminri=imin∥w∥2∣∣wTxi+b∣∣ -
SVM目标函数
max w , b M max w , b { min i ∣ w T x i + b ∣ ∥ w ∥ 2 } \begin{array}{c}{\max _{\mathbf{w}, b} M} \\ {\max _{\mathbf{w}, b}\left\{\min _{i} \frac{\left|\mathbf{w}^{T} \mathbf{x}_{i}+b\right|}{\|\mathbf{w}\|_{2}}\right\}}\end{array} maxw,bMmaxw,b{mini∥w∥2∣wTxi+b∣}
4.3 简化目标函数
-
分子部分 w T x i + b \mathbf{w^Tx_i}+b wTxi+b可以改写为:
y i ( w T x i + b ) y_i(\mathbf{w^Tx_i}+b) yi(wTxi+b)- y i y_i yi是人为定义的 y i ∈ { 1 , − 1 } y_i \in \{1,-1\} yi∈{1,−1}
- 如果 w T x i + b > 0 \mathbf{w^Tx_i}+b>0 wTxi+b>0,则 y i = 1 y_i=1 yi=1;
- 如果 w T x i + b < 0 \mathbf{w^Tx_i}+b<0 wTxi+b<0,则 y i = − 1 y_i=-1 yi=−1;
- 目标函数由 max w , b { min i ∣ w T x i + b ∣ ∥ w ∥ 2 } {\max _{\mathbf{w}, b}\left\{\min _{i} \frac{\left|\mathbf{w}^{T} \mathbf{x}_{i}+b\right|}{\|\mathbf{w}\|_{2}}\right\}} maxw,b{mini∥w∥2∣wTxi+b∣}变为:
max w , b { min i y i ( w T x i + b ) ∥ w ∥ 2 } {\max _{\mathbf{w}, b}\left\{\min _{i} \frac{ y_i(\mathbf{w}^{T} \mathbf{x}_{i}+b)}{\|\mathbf{w}\|_{2}}\right\}} w,bmax{imin∥w∥2yi(wTxi+b)}
- 上述目标函数中,大括号里边是对i进行遍历,与w无关,因此目标函数可以写成:
max w , b { 1 ∥ w ∥ 2 min i y i ( w T x i + b ) } \max _{\mathbf{w}, b}\left\{\frac{1}{\|\mathbf{w}\|_{2}} \min _{i} y_{i}\left(\mathbf{w}^{T} \mathbf{x}_{i}+b\right)\right\} w,bmax{∥w∥21iminyi(wTxi+b)}
-
进行scaling, w → k w \mathbf{w} \rightarrow k\mathbf{w} w→kw和 b → k b b \rightarrow kb b→kb,将这两个参数分别缩放后,我们可以知道点到平面的距离不变。(分子分母同时提出一个k)
-
因此,我们可以设计距离最近的一个点,使得 y i ( w T x i + b ) = 1 y_i(\mathbf{w}^{T} \mathbf{x}_{i}+b)=1 yi(wTxi+b)=1
-
同时有
y i ( w T x i + b ) ≥ 1 i = 1 , 2 , 3... N y_i(\mathbf{w}^{T} \mathbf{x}_{i}+b) \ge1 \quad i=1,2,3...N yi(wTxi+b)≥1i=1,2,3...N -
因此目标函数变为
-
max w , b { 1 ∥ w ∥ 2 ∗ 1 } → max w , b { 1 ∥ w ∥ 2 } → min w , b { 1 2 ∣ w ∥ 2 2 } s . t . y i ( w T x i + b ) ≥ 1 i = 1 , 2 , 3... N \max _{\mathbf{w}, b}\left\{\frac{1}{\|\mathbf{w}\|_{2}} *1\right\} \rightarrow \max _{\mathbf{w}, b}\left\{\frac{1}{\|\mathbf{w}\|_{2}}\right\} \rightarrow \min _{\mathbf{w}, b}\{{\frac{1}{2}|\mathbf{w}\|_{2}^{2}}\}\\s.t. \quad y_i(\mathbf{w}^{T} \mathbf{x}_{i}+b) \ge1 \quad i=1,2,3...N w,bmax{∥w∥21∗1}→w,bmax{∥w∥21}→w,bmin{21∣w∥22}s.t.yi(wTxi+b)≥1i=1,2,3...N
-
约束条件的解释:对于距离最近的点,取等号;其余点均取大于号
五:SVM求解
回想QP问题的标准型:
minimize 1 2 x T P x + c T x + d subject to G x ≤ h A x = b \begin{array}{cl}{\operatorname{minimize}} & {\frac{1}{2} \mathbf{x}^{T} \mathbf{P} \mathbf{x}+\mathbf{c}^{T} \mathbf{x}+d} \\ {\text { subject to }} & {\mathbf{G} \mathbf{x} \leq \mathbf{h}} \\ {} & {\mathbf{A x}=\mathbf{b}}\end{array} minimize subject to 21xTPx+cTx+dGx≤hAx=b
那么SVM问题就是一个典型的QP问题:
minimize 1 2 ∥ w ∥ 2 2 + C ∑ i = 1 N ξ i subject to y i ( w T x i + b ) ≥ 1 − ξ i , i = 1 , ⋯ , N ξ i ≥ 0 \begin{array}{ll}{\text { minimize }} & {\frac{1}{2}\|\mathbf{w}\|_{2}^{2}+C \sum_{i=1}^{N} \xi_{i}} \\ {\text { subject to }} & {y_{i}\left(\mathbf{w}^{T} \mathbf{x}_{i}+b\right) \geq 1-\xi_{i}, i=1, \cdots, N} \\ {} & {\xi_{i} \geq 0}\end{array} minimize subject to 21∥w∥22+C∑i=1Nξiyi(wTxi+b)≥1−ξi,i=1,⋯,Nξi≥0
其中,存在$ \xi_{i} 是 软 间 隔 ( 此 时 可 以 假 设 是软间隔(此时可以假设 是软间隔(此时可以假设\xi_i=0$。此时需要注意的是,我们并不知只有一个约束条件,而是存在N个约束条件。也就是说,有多少个样本点,我们就有多少个约束条件。当样本点特别大时,计算会变得非常慢。因此,我们考虑他的对偶问题。目标函数是凸函数,约束条件为线性,所以是一个凸优化问题,因此是一个强对偶问题。也就是说对偶问题的最大值就是原问题的最小值。
5.1 SVM对偶问题
-
拉格朗日函数:
L ( w , b , λ ) = 1 2 ∥ w ∥ 2 2 + ∑ i = 1 N λ i ( 1 − y i ( w T x i + b ) ) L(\mathbf{w}, b, \boldsymbol{\lambda})=\frac{1}{2}\|\mathbf{w}\|_{2}^{2}+\sum_{i=1}^{N} \lambda_{i}\left(1-y_{i}\left(\mathbf{w}^{T} \mathbf{x}_{i}+b\right)\right) L(w,b,λ)=21∥w∥22+i=1∑Nλi(1−yi(wTxi+b)) -
对偶问题为:
g ( λ ) = min w , b L ( w , b , λ ) g(\boldsymbol{\lambda})=\min_{\mathbf{w},b} L(\mathbf{w}, b, \boldsymbol{\lambda}) g(λ)=w,bminL(w,b,λ) -
所以对偶问题的最优值为:
d ∗ = max λ g ( λ ) = max λ { min w , b L ( w , b , λ ) } d^*=\max_{\boldsymbol{\lambda}}g(\boldsymbol{\lambda})=\max_{\boldsymbol{\lambda}}\{\min_{\mathbf{w},b} L(\mathbf{w}, b, \boldsymbol{\lambda})\} d∗=λmaxg(λ)=λmax{w,bminL(w,b,λ)}
令 L ( w , b , λ ) L(\mathbf{w}, b, \boldsymbol{\lambda}) L(w,b,λ)对 w , b \mathbf{w},b w,b分别求导,可以得到:
L ′ ( w ) = w − ∑ i = 1 N λ i y i x i = 0 所 以 w = ∑ i = 1 N λ i y i x i L'(\mathbf{w}) = \mathbf{w} -\sum_{i=1}^{N}\lambda_iy_i\mathbf{x}_i=0\\所以\mathbf{w} =\sum_{i=1}^{N}\lambda_iy_i\mathbf{x}_i L′(w)=w−i=1∑Nλiyixi=0所以w=i=1∑NλiyixiL ′ ( b ) = ∑ i = 1 N λ i y i = 0 L'(b)=\sum_{i=1}^{N} \lambda_{i} y_{i}=0 L′(b)=i=1∑Nλiyi=0
将以上两个式子代入对偶问题:则对偶问题的最优值变为:
max λ ∑ i = 1 N λ i − 1 2 ∑ i = 1 N ∑ j = 1 N λ i λ j y i y j x i T x j subject to ∑ i = 1 N λ i y i = 0 , λ i ≥ 0 , i = 1 , ⋯ , N \begin{array}{cl}{\max _{\lambda}} & {\sum_{i=1}^{N} \lambda_{i}-\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \lambda_{i} \lambda_{j} y_{i} y_{j} \mathbf{x}_{i}^{T} \mathbf{x}_{j}} \\ {\text { subject to }} & {\sum_{i=1}^{N} \lambda_{i} y_{i}=0, \lambda_{i} \geq 0, i=1, \cdots, N}\end{array} maxλ subject to ∑i=1Nλi−21∑i=1N∑j=1NλiλjyiyjxiTxj∑i=1Nλiyi=0,λi≥0,i=1,⋯,N
我们假设能够解出 λ ∗ \lambda_* λ∗,根据KKT条件有:
y i ( w ∗ T x i + b ∗ ) ≥ 1 λ i ∗ ≥ 0 λ i ∗ ( y i ( w ∗ T x i + b ∗ ) − 1 ) = 0 w ∗ = ∑ i = 1 N λ i ∗ y i x i , ∑ i = 1 N λ i ∗ y i = 0 \begin{array}{l}{y_{i}\left(\mathbf{w}^{* T} \mathbf{x}_{i}+b^{*}\right) \geq 1} \\ {\lambda_{i}^{*} \geq 0} \\ {\lambda_{i}^{*}\left(y_{i}\left(\mathbf{w}^{* T} \mathbf{x}_{i}+b^{*}\right)-1\right)=0} \\ {\mathbf{w}^{*}=\sum_{i=1}^{N} \lambda_{i}^{*} y_{i} \mathbf{x}_{i}, \sum_{i=1}^{N} \lambda_{i}^{*} y_{i}=0}\end{array} yi(w∗Txi+b∗)≥1λi∗≥0λi∗(yi(w∗Txi+b∗)−1)=0w∗=∑i=1Nλi∗yixi,∑i=1Nλi∗yi=0
仔细观察上述条件:我们可以得出以下结论:-
如果 λ ∗ = 0 \lambda^* =0 λ∗=0,那么 λ \lambda λ对 w \mathbf{w} w没有贡献。
-
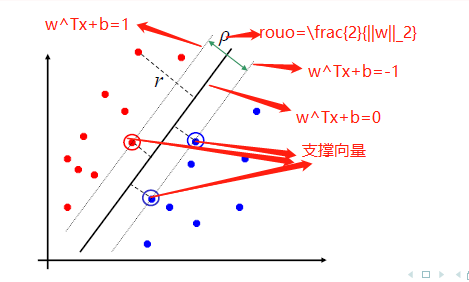
如果 λ ∗ > 0 \lambda^* >0 λ∗>0,那么 y i ( w ∗ T x i + b ∗ ) = 1 y_{i}\left(\mathbf{w}^{* T} \mathbf{x}_{i}+b^{*}\right)=1 yi(w∗Txi+b∗)=1,称这些点为支撑向量。
-
所以 w ∗ \mathbf{w}^* w∗只与那些 λ ≠ 0 , y i ( w ∗ T x i + b ∗ ) = 1 \lambda \neq0,y_{i}\left(\mathbf{w}^{* T} \mathbf{x}_{i}+b^{*}\right)=1 λ̸=0,yi(w∗Txi+b∗)=1的点有关。把 w ∗ = ∑ i = 1 N λ i ∗ y i x i \mathbf{w}^{*}=\sum_{i=1}^{N} \lambda_{i}^{*} y_{i} \mathbf{x}_{i} w∗=∑i=1Nλi∗yixi代入 y i ( w ∗ T x i + b ∗ ) = 1 y_{i}\left(\mathbf{w}^{* T} \mathbf{x}_{i}+b^{*}\right)=1 yi(w∗Txi+b∗)=1中,可以得到 b ∗ = y i − ∑ i = 1 N λ i ∗ y i ( x i T x i ) b^{*}=y_{i}-\sum_{i=1}^{N} \lambda_{i}^{*} y_{i}\left(\mathbf{x}_{i}^{T} \mathbf{x}_{i}\right) b∗=yi−∑i=1Nλi∗yi(xiTxi)
-
从以上可以得出一点:
- 在求 λ \lambda λ的过程中,所有点都有作用。但是在求解之后,可以只保留支撑向量点。因为非支撑像向量点的 λ = 0 \lambda =0 λ=0,对 w \mathbf{w} w的求解没有帮助。
5.2 最优的分离超平面及决策函数
-
分离超平面:
w ∗ T x + b ∗ = 0 ∑ i = 1 N λ i ∗ y i x i T x + b ∗ = 0 \begin{array}{c}{\mathbf{w}^{* T} \mathbf{x}+b^{*}=0} \\ {\sum_{i=1}^{N} \lambda_{i}^{*} y_{i} \mathbf{x}_{i}^{T} \mathbf{x}+b^{*}=0}\end{array} w∗Tx+b∗=0∑i=1Nλi∗yixiTx+b∗=0 -
决策函数
f ( x ) = sign ( ∑ i = 1 N λ i ∗ y i x i T x + b ∗ ) f(\mathbf{x})=\operatorname{sign}\left(\sum_{i=1}^{N} \lambda_{i}^{*} y_{i} \mathbf{x}_{i}^{T} \mathbf{x}+b^{*}\right) f(x)=sign(i=1∑Nλi∗yixiTx+b∗)
需要注意的是:支持向量机无法像逻辑回归那样,给出一个分类的概率,只能告诉你,样本被分为哪一类。
六:软间隔问题
在上述的SVM求解问题当中,我们要求所有的样本点都要划分正确,不允许出现错误,但是在实际的分类任务中,我们可以适当地允许一些样本点犯错,牺牲了在某些样本点上必须分类正确地限制,来换取更大的分类间隔。软间隔SVM问题的表示形式如下:
minimize 1 2 ∥ w ∥ 2 2 + C ∑ i = 1 N ξ i subject to y i ( w T x i + b ) ≥ 1 − ξ i , i = 1 , ⋯ , N ξ i ≥ 0 \begin{array}{ll}{\operatorname{minimize}} & {\frac{1}{2}\|\mathbf{w}\|_{2}^{2}+C \sum_{i=1}^{N} \xi_{i}} \\ {\text { subject to }} & {y_{i}\left(\mathbf{w}^{T} \mathbf{x}_{i}+b\right) \geq 1-\xi_{i}, i=1, \cdots, N} \\ {} & {\xi_{i} \geq 0}\end{array} minimize subject to 21∥w∥22+C∑i=1Nξiyi(wTxi+b)≥1−ξi,i=1,⋯,Nξi≥0
在上述的表示当中,我们把错误记录在一个 ξ i \xi_i ξi中,这个变量记录了样本点 ( x i , y i ) (x_i,y_i) (xi,yi)犯了多大的错。然后在目标函数中优化 ∑ i = 1 n ξ i \sum_{i=1}^{n}\xi_i ∑i=1nξi,以使得所犯的错误最小。
那么为什么 ξ i \xi_i ξi可以用来表示样本点犯错的大小呢?如果 y i ( w T x i + b ) ≥ 1 y_{i}\left(\mathbf{w}^{T} \mathbf{x}_{i}+b\right) \geq 1 yi(wTxi+b)≥1,那么说明样本点没有分类错误,对应的 ξ i = 0 \xi_i=0 ξi=0,如果 y i ( w T x i + b ) < 1 y_{i}\left(\mathbf{w}^{T} \mathbf{x}_{i}+b\right) < 1 yi(wTxi+b)<1,说明样本点被分类错误,分类错误的程度 ξ i = 1 − y i ( w T x i + b ) \xi_i = 1-y_{i}\left(\mathbf{w}^{T} \mathbf{x}_{i}+b\right) ξi=1−yi(wTxi+b)。比如:某个样本点的 y i ( w T x i + b ) = − 10 y_{i}\left(\mathbf{w}^{T} \mathbf{x}_{i}+b\right) = -10 yi(wTxi+b)=−10,则相应的 ξ i = 1 − ( − 10 ) = 11 \xi_i=1-(-10)=11 ξi=1−(−10)=11.
参数C的作用:
- C大,说明我们更在意分类的准确性,间隔可以小一点,但是划分错误的点要少一些。
- C小,则表明我们可以要“胖”一点的间隔,划分错误的点多一些没有关系。
七:核函数
需要注意的是,在实际的分类任务中,并不是所有任务都是线性可分的,如下图所示:
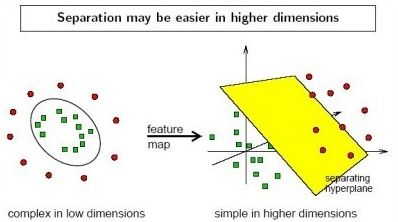
我们可以通过特征映射的方式,将样本点映射到高维空间中,找到一个超平面进行切分。映射方式为 x → ψ ( x ) x \rightarrow \psi(x) x→ψ(x)。则支持向量机的目标变为:
m i n 1 2 ∥ w ∥ 2 2 subject to y i ( w T ϕ ( x i ) + b ) ≥ 1 , i = 1 , ⋯ , N \begin{array}{ll}min & {\frac{1}{2}\|\mathbf{w}\|_{2}^{2}} \\ {\text { subject to }} & {y_{i}\left(\mathbf{w}^{T} \phi\left(\mathbf{x}_{i}\right)+b\right) \geq 1, \quad i=1, \cdots, N}\end{array} min subject to 21∥w∥22yi(wTϕ(xi)+b)≥1,i=1,⋯,N
特征映射 x → ψ ( x ) x \rightarrow \psi(x) x→ψ(x),所以对偶问题是:
max λ ∑ i = 1 N λ i − 1 2 ∑ i = 1 N ∑ j = 1 N λ i λ j y i y j ϕ ( x i ) T ϕ ( x j ) subject to ∑ i = 1 N λ i y i = 0 , λ i ≥ 0 , i = 1 , ⋯ , N \begin{array}{ll}{\max _{\lambda}} & {\sum_{i=1}^{N} \lambda_{i}-\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \lambda_{i} \lambda_{j} y_{i} y_{j} \phi\left(\mathbf{x}_{i}\right)^{T} \phi\left(\mathbf{x}_{j}\right)} \\ {\text { subject to }} & {\sum_{i=1}^{N} \lambda_{i} y_{i}=0, \lambda_{i} \geq 0, i=1, \cdots, N}\end{array} maxλ subject to ∑i=1Nλi−21∑i=1N∑j=1Nλiλjyiyjϕ(xi)Tϕ(xj)∑i=1Nλiyi=0,λi≥0,i=1,⋯,N
直接计算 ϕ ( x i ) T ϕ ( x j ) \phi\left(\mathbf{x}_{i}\right)^{T} \phi\left(\mathbf{x}_{j}\right) ϕ(xi)Tϕ(xj)是非常困难的,因此我们设定一个函数:
κ ( x i , x j ) = ϕ ( x i ) T ϕ ( x j ) \kappa\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)=\phi\left(\mathbf{x}_{i}\right)^{T} \phi\left(\mathbf{x}_{j}\right) κ(xi,xj)=ϕ(xi)Tϕ(xj)
这样便可以解决上述问题,因此决策函数变为:
f ( x ) = sign ( ∑ i = 1 N λ i ∗ y i ϕ ( x i ) T ϕ ( x ) + b ∗ ) = sign ( ∑ i = 1 N λ i ∗ y i κ ( x i , x ) + b ∗ ) f(\mathbf{x})=\operatorname{sign}\left(\sum_{i=1}^{N} \lambda_{i}^{*} y_{i} \phi(\mathbf{x}_{i})^{T} \phi(\mathbf{x})+b^{*}\right)\\=\operatorname{sign}\left(\sum_{i=1}^{N} \lambda_{i}^{*} y_{i}\kappa\left(\mathbf{x}_{i}, \mathbf{x}\right) +b^{*}\right) f(x)=sign(i=1∑Nλi∗yiϕ(xi)Tϕ(x)+b∗)=sign(i=1∑Nλi∗yiκ(xi,x)+b∗)
常用的核函数:
-
线性核: κ ( x i , x j ) = x i T x j \kappa\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)=\mathbf{x}_{i}^{T} \mathbf{x}_{j} κ(xi,xj)=xiTxj
-
多项式核: κ ( x i , x j ) = ( x i T x j ) d , d ≥ 1 \kappa\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)=\left(\mathbf{x}_{i}^{T} \mathbf{x}_{j}\right)^{d}, d \geq 1 κ(xi,xj)=(xiTxj)d,d≥1
-
高斯核: κ ( x i , x j ) = exp ( − ∥ x i − x j ∥ 2 2 σ 2 ) \kappa\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)=\exp \left(-\frac{\left\|\mathbf{x}_{i}-\mathbf{x}_{j}\right\|^{2}}{2 \sigma^{2}}\right) κ(xi,xj)=exp(−2σ2∥xi−xj∥2)
八:参考资料
- https://blog.csdn.net/han_xiaoyang/article/details/52678373
- https://blog.csdn.net/robin_xu_shuai/article/details/76946333
- 稀牛学院&网易云课堂《人工智能数学基础》