【论文笔记】FCN
《Fully Convolutional Networks for Semantic Segmentation》,CVPR 2015
文章目录
- 1. 概览
- 2. 主要亮点
- 2.1 全卷积化
- 2.2 反卷积 / 上采样
- 2.3 跃层结构
- 3. 网络结构
- 3.1 voc-fcn-alexnet
- 3.2 voc-fcn32s
- 3.3 fcn16s
- 3.4 fcn8s
- 4. 关于细节的解释
- 4.1 全连接层到卷积层
- 4.2 关于跃层结构
1. 概览
论文核心思想: 建立全卷积网络,使其可以输入任意大小的图片,并输出一个与原图像大小相同的像素级分类结果,即 dense prediction。
论文所采用的经典分类网络:
- AlexNet
- VGGNet
- GoogLeNet
将这三种网络改造成全卷积网络,将它们学习的特征表示经过 fine-tuning 转换到分割任务上来。
【论文中提到,经过改造后,达到最高分类精度的是 VGG-16】
论文所采用的数据集:
- PASCAL VOC
- NYUDv2
- SIFT Flow
什么是 spatially dense prediction task?就是需要对图像中所有像素点进行分类的任务。图像的语义分割 简而言之就是对一张图片上的所有像素点进行分类,所以这就属于 spatially dense prediction task。
FCN 的优势和不足
FCN 的优势在于:
- 可以接受任意大小的输入图像(没有全连接层)
- 更加高效,避免了使用邻域带来的重复计算和空间浪费的问题。
其不足也很突出:
- 结果不够精细 ,进行8倍上采样虽然比32倍的效果好了很多,但是上采样的结果还是比较模糊,对图像中的细节不敏感。
- 是对各个像素进行分类,没有充分考虑像素与像素之间的关系,缺乏空间一致性。
2. 主要亮点
2.1 全卷积化
用卷积层替换全连接层
经典 CNN 在卷积层之后接上若干全连接层,全连接层将卷积产生的特征图映射成一个固定长度的特征向量,期望用这个特征向量得到一个对整张图像的数值描述(分类概率)。
比如:AlexNet 最后就会输出一个 1000 维的向量表示图像属于每一类的概率(full connection + softmax,用 softmax 进行归一化)
改进的 FCN 做出了如下操作:
1)FCN 将 CNN 最后的全连接层替换为卷积层,可以接受任意尺寸的输入图像;
2)利用反卷积层对最后一个卷积层的特征图(heatmap)进行上采样,使它恢复到与原图相同的尺寸,这样就保留了原始图像的空间信息,然后可以在上采样得到的特征图上逐像素进行分类,从而能够对原图的每一个像素都进行预测,最后再逐个像素计算 softmax 分类的损失;
FCN 对图像实际进行了像素级别的分类,将每个像素都看作一个训练样本,不仅要预测其类别,还要计算其 softmax 分类的损失。这一进展解决了语义级别的图像分割问题。
注意:计算损失时是对每个像素使用 softmax loss,最终总的 loss 是所有像素的 loss 和
在论文中用这张图表示传统 CNN 的输出与 FCN 的输出对比:
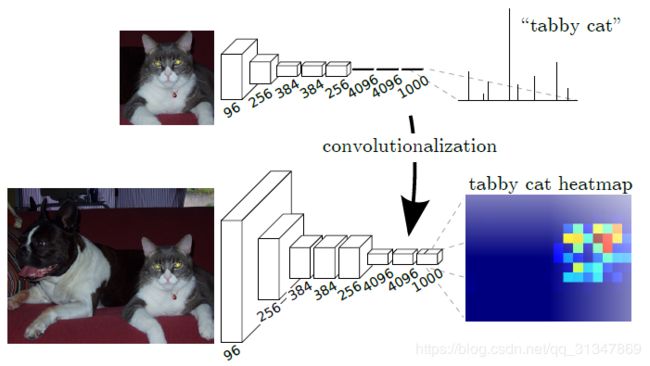
2.2 反卷积 / 上采样
顺用 VGG 的结构,先下采样后再上采样,恢复到原图大小。
2.3 跃层结构
将来自深层(粗层)的语义信息和来自浅层(细层)的外观信息结合起来,得到更加精确和鲁棒的分割结果。

使用跃层结构融合多层输出,使得网络能够预测更多的位置信息。因为在浅层网络位置信息等保留的比较好,将他们加入到深层输出中,就可以预测到更精细的信息。
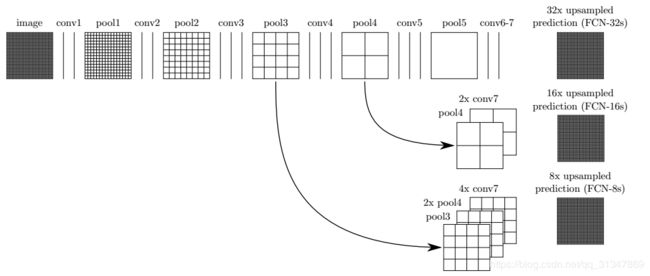
3. 网络结构
3.1 voc-fcn-alexnet
由 AlexNet 改造得到该网络,从 conv1 到 pool5 照搬 AlexNet,将 fc6 和 fc7 改造为卷积层,该网络不包含跃层结构。
网络定义文件参考:caffe/fcn-master/voc-fcn-alexnet/train.prototxt
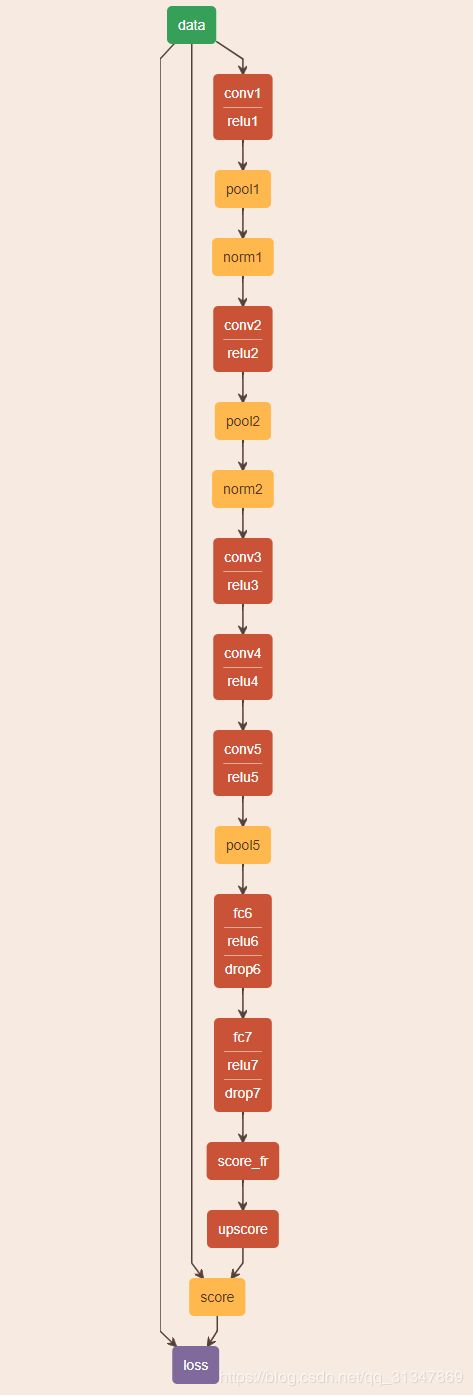
假设输入一张大小为 500 * 500 的图像,那么经过网络处理的过程如下:(省略掉了不使尺寸发生改变的 relu、norm 和 dropout 层)

3.2 voc-fcn32s
voc-fcn32s 的网络结构定义参考源代码:caffe/fcn-master/voc-fcn32s/train.prototxt

- 从
conv1_1到pool5都是照搬 VGG16 的网络结构 - 将
fc6-4096和fc7-4096都改成了卷积层,而且还各自加了一个Dropout层 score_fr是最后一个卷积层,该层的输出叫 heatmap(热图),其实就是 feature map,但它是最重要的高维特征图,在得到这个高维特征图后,就要对其进行反卷积,将图像进行放大- 看到网络结构里
score_fr的输出通道数是 21,这是因为 VOC 数据集有 21 类,所以实际上最后一个卷积层score_fr输出的是 21 个通道的高维特征图
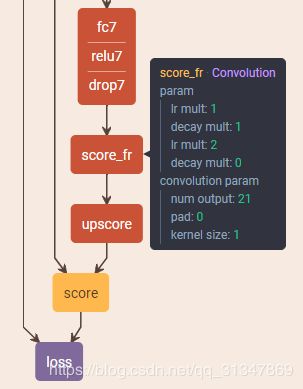
- 将
score_fr的输出特征图通过反卷积层upscore放大 32 倍

- 最后通过 crop 层将放大了 32 倍的特征图裁剪到与原图相同的大小,参考:Crop层的作用
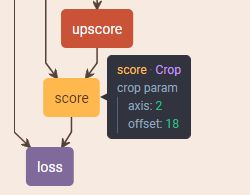
- 得到与原图大小相同的特征图后,就要为每个像素计算分别属于 21 个类的概率,这里使用的是 softmax,最后通过 label 计算 loss,从网络结构上看出 caffe 将 softmax 和 loss 的计算合并为了一层
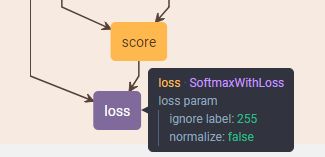
假设输入一张大小为 500 * 500 的图像,那么经过网络处理的过程如下(conv层不使特征图大小发生改变,所以合并了同属一组的conv层):
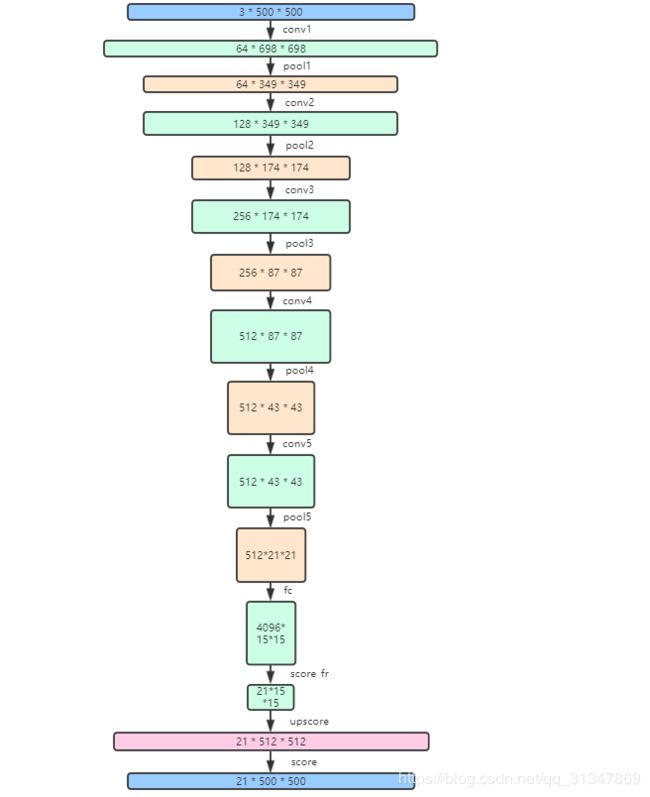
- fc 的输出特征图大小是原始图像的 1/32,通过上采样 upscore 将其放大,最后由 crop 裁剪到原图大小
3.3 fcn16s
- fcn16s 和 fcn32s 类似,只是加入了跃层结构,
score_fr得到最终的 heatmap,这一点和 fcn32s 相同

- upscore2 对 heatmap 进行反卷积,将其放大 2 倍,为了下面和 pool4 的输出进行连接

- 在 pool4 后输出一张特征图,并额外添加一层
score_pool4用于生成 pool4 的输出 heatmap,这一层是 32s 没有的 score_pool4c为 Crop 层,它将score_pool4输出的特征图 crop 到与upscore2相同的形状fuse_pool4为 Eltwise 层,其作用是融合数据,也就是论文中说的将 pool4 的输出特征图与 heatmap 做融合,执行的操作是score_pool4c + upscore2参考:Caffe layer:Eltwise
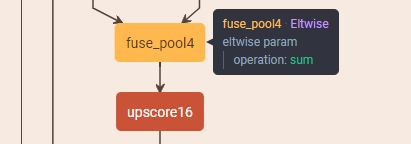
upscore16层又是反卷积,将融合的特征图放大 16 倍(前面已经放大了 2 倍,这里再放大 16 倍就相当于放大了 16 * 2 = 32 倍,和 32s 效果一样,都能回到原图大小)

score为 Crop 层,将上一层放大了的特征图 crop 到与原图大小相同的形状

- 最后 softmax 计算每个像素的概率,并计算 loss
3.4 fcn8s

和 16s 的原理一样,将 pool3 和 pool4 的输出特征图与最后的 heatmap 相融合,在下面三处反卷积层对特征图进行放大,放大倍数分别为 2,2,8。



4. 关于细节的解释
为什么 FCN 的输入图片可以是任意大小的?
因为卷积网络的参数只与卷积核的大小和输入输出的channel数有关,和图像的尺寸没关系。
卷积层和全连接层的唯一区别在于卷积层的神经元对输入是局部连接的,并且同一个通道(channel)内不同神经元共享权值(weights).
卷积层和全连接层都是进行了一个点乘操作, 它们的函数形式相同. 因此卷积层可以转化为对应的全连接层, 全连接层也可以转化为对应的卷积层.
举个例子:
VGGNet中, 第一个全连接层的输入是77512, 输出是4096. 这可以用一个卷积核大小77, 步长(stride)为1, 没有填补(padding), 输出通道数4096的卷积层等效表示, 其输出为11*4096, 和全连接层等价. 后续的全连接层可以用1x1卷积等效替代。
全连接层转化为卷积层的规则是: 将卷积核大小设置为输入的空间大小.这样做的好处在于卷 积层对输入大小没有限制, 因此可以高效地对测试图像做滑动窗式的预测。
如何生成 dense prediction?
作者对比了 3 种方案:
- shift and stitch
- decreasing subsampling
- deconvolution
最终作者采用了第三种方法:deconvolution
shift and stitch:fileds 无法感受更精细的信息
decreasing subsampling:filters 可以看到更精细的信息,但同时 receptive fields 感受野也更小,可能损失全局 信息,而且计算花费大
deconvolution:反卷积其实就是 upsampling(上采样)
为什么要上采样?
上采样其实就是为了得到一张和原图大小相同的输出图
为什么要将 CNN 改进为 FCN?
首先 CNN 本身就很强大,它的多层结构不仅能自动学习特征,还能学到很多层次的特征。其中:
较浅的卷积层感受野较小,学习局部特征;
较深的卷积层感受野较大,学习更全局的特征,即更加抽象的特征。
1)参数量太大
假如输入10001000像素的图片,即输入层有10001000个节点。假设第一个隐藏层有100个节点(这个数量并不多),那么仅这一层就有(1000*1000+1)*100=1亿参数,这实在是太多了!我们看到图像只扩大一点,参数数量就会多很多,因此它的扩展性很差。
2)没有利用像素之间的位置信息
对于图像识别,每个像素和其周围的像素的联系都是比较紧密的,和离得远的像素的联系可能就很小。如果一个神经元和上一层所有神经元相连,那么就相当于对于一个像素来说,把图像的所有像素都等同看待,这不符合前面的假设。当我们完成每个连接权重的学习之后,最终可能会发现,有大量的权重,它们的值都是很小的(也就是这些连接其实无关紧要)。努力学习大量并不重要的权重,这样的学习必将是非常低效的。
3)网络层数限制
一般而言网络层数越多表达能力越强。但是通过梯度下降的方法训练神全连接神经网络很困难,因为全连接神经网络的梯度很难传递超过3层。因此,我们不可能得到一个很深的全连接神经网络,也就限制了它的能力。
对于卷积神经网络解决以上三个问题,主要有三个思路:
- 局部连接
这个是最容易想到的,每个神经元不再和上一层的所有神经元相连,而只和一小部分神经元相连。这样就减少了很多参数。 - 权值共享
一组连接可以共享同一个权重,而不是每个连接有一个不同的权重,这样又减少了很多参数。 - 下采样
可以使用Pooling来减少每层的样本数,进一步减少参数数量,同时还可以提升模型的鲁棒性。
学习抽象特征有什么好处?
抽象特征对物体的大小、位置、方向的敏感性低,也就是这些因素对特征的影响不大,有助于识别性能的提高。
不过学习抽象特征也有劣势,就是丢掉了物体的细节,不能很好地给出物体的具体轮廓、支出每个像素具体地属于哪个物体,所以不太适合精细的分割任务。
所以传统的分割方法虽然有 CNN,但不是基于特征的:
为了对一个像素分类,使用该像素周围的一个图像块作为CNN的输入用于训练和预测。这种方法有几个缺点:一是存储开销很大。例如对每个像素使用的图像块的大小为15x15,然后不断滑动窗口,每次滑动的窗口给 CNN 进行判别分类,因此则所需的存储空间根据滑动窗口的次数和大小急剧上升。二是计算效率低下。相邻的像素块基本上是重复的,针对每个像素块逐个计算卷积,这种计算也有很大程度上的重复。三是像素块大小的限制了感知区域的大小。通常像素块的大小比整幅图像的大小小很多,只能提取一些局部的特征,从而导致分类的性能受到限制。
但是,既然抽象的特征对分类一整张图片有好处,那么对于分类像素应该也是有帮助的。
所以提出基于特征的分割方法:全卷积网络
FCN 从抽象的特征中恢复出每一个像素所属的类别,实现从图像级别的分类到像素级别的分类。
4.1 全连接层到卷积层
全连接层和卷积层的唯一不同之处在于:
全连接层的每个神经元会和上一层所有神经元相连
而卷积层中的每个神经元只和上一层的一个局部区域相连
但是,两种层都是在神经元之间计算点积,函数形式其实是一样的,所以两者是可以互相转换的。
卷积层 -> 全连接层:
全连接层 -> 卷积层:
输入数据尺寸 7*7*512,经过一个全连接层得到 1*1*4096 的输出,此时全连接层就能看作是一个 kernel size = 7,stride = 1,padding = 0,channel = 512,number = 4096 的卷积层
也就是卷积核尺寸 = 输入数据尺寸
AlexNet 最后是两个尺寸为 4096 的全连接层,再加一个尺寸为 1000 的全连接层用于计算类别得分。可以将这 3 个全连接层的任意一层转换为卷积层:
- 对第一个连接域是 7*7*512 的全连接层,令替代的卷积操作 kernel size = 7*7*512,共 4096 个滤波器,就能得到输出尺寸为 1*1*4096 的输出数据
- 对于第二个全连接层,令替代的卷积操作 kernel size = 1*1*4096,共 4096 个滤波器,就能得到输出尺寸为 1*1*4096 的输出数据
- 对于第三个全连接层,令替代的卷积操作 kernel size = 1*1*4096,共 1000 个滤波器,就能得到输出尺寸为 1*1*1000 的输出数据
所以将全连接层换成卷积层有什么好处?
卷积网络可以在一张更大的输入图片上滑动,得到多个输出
比如:
对于一张 384384 的输入图像,用 CNN 的全连接层以 kernel size = 224224,stride = 32
也就是说,用卷积得到的结果与全连接是一样的,但是优点在于…
CNN 需要将输入图像的尺寸固定为 227227,第一层 pooling 后为 5555,第二层 pooling 后为 2727,…,第五层 pooling 后为 1313
而 FCN 输入图像的大小任意,第一层 pooling 后变为原图大小的 1/4,第二层 pooling 后变为原图大小的 1/8,…,第五层 pooling 后变为原图大小的 1/16,第八层 pooling 后变为原图大小的 1/32。(在实际代码中第一层其实是 1/2,后面一次类推)
经过多次卷积和 pooling 以后,得到的图像越来越小,分辨率越来越低。pooling 到 H/32∗W/32 的时候是最小的一层时,所产生图叫做heatmap,热图就是最重要的高维特征图,得到高维特征的heatmap 之后就是最重要的一步,也是最后一步:对 heatmap 进行 upsampling,把图像放大到原图像的大小。
最后的输出是 1000 张 heatmap 经过 upsampling 变为原图大小的图片,对每个像素进行类别预测,通过逐个像素地求其在 1000 张图像该像素位置的最大数值描述(概率)作为该像素的分类。
跃层结构:
- 对原图进行 conv1、pool1 后图像缩小为原图的 1/2
- 进行 conv2、pool2,图像缩小为原图的 1/4
- 进行 conv3、pool3,图像缩小为原图的 1/8,此时保留 pool3 的输出结果(特征图)
- 进行conv4、pool4,图像缩小为原图的 1/16,此时保留 pool4 的输出结果(特征图)
- 进行 conv5、pool5,图像缩小为原图的 1/32
- 将原全连接层变成卷积操作的 conv6、conv7,输出的特征图大小仍为原图的 1/32,这时输出不叫 feature map 而叫 heat map
为什么要这样做?
直接将第 pool5 的输出反卷积到原图大小不是很精确,一些细节无法恢复,所以将其前一层 pool4 的输出和 pool3 的输出也都反卷积一下,分别需要 16 倍和 8 倍的上采样,这样将它们连接起来得到的结果就能更精细一些,同时兼顾了局部和全局。

反向传播:
FCN 网络的输入 batch size = 1,因为分割任务一张图片中每个像素点都有 ground truth,相当于每一个像素点就是一个分类任务,那么一张图像中的样本数量就是像素点总数
所以分割任务的 batch 就是一张图片,将一张图片在所有像素点上分类的 loss 加起来后,计算一次梯度的更新,进行反向传播。
训练过程:
来自文章:https://blog.csdn.net/qq_36269513/article/details/80420363
训练过程分为 4 个阶段:
第一阶段

以经典的分类网络为基础进行初始化,这里给出的是 AlexNet 模型,最后两层为全连接层(红色部分),参数丢掉不用。
第二阶段
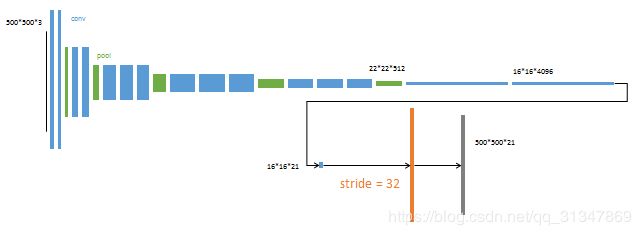
pool5 的输出尺寸为 22*22*512,再经过改造的两个卷积层输出 16*16*4096 的特征图,用该特征图预测一个分割的小图 16*16*21(因为用的是 PASCAL VOC 数据集,所以有 20 个类外加一个背景类),再将这个小图上采样为与原图大小相同的分割结果。
由于反卷积(橙色部分)的 stride 为 32,所以该网络叫做 FCN-32s。
第二阶段使用单 GPU 训练约需要 3 天
第三阶段

上采样分为两次完成(橙色部分)
第一次上采样的结果保持不变
将 pool4 的输出结果也进行上采样,得到一个预测结果(蓝色)
,将这个预测结果融合进第一次上采样的结果。
使用该跃层结构能够提升精确性
由于第二次反卷积的 stride 为 16,所以该网络叫做 FCN-16s
第三阶段使用单 GPU 训练约需要 1 天
第四阶段

上采样分三次完成(橙色部分 * 3)
第一步融合了三个 pooling 层的预测结果
由于第三次反卷积步长为 8,所以该网络叫做 FCN-8s
第四阶段使用单 GPU 训练约需要 1 天
所以说,跃层结构就是在结合浅层信息,逐步生成更精细的结果。
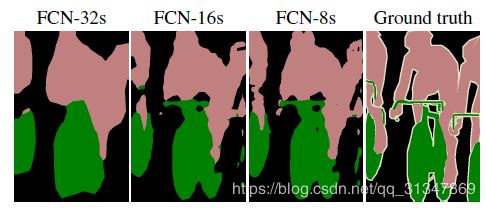
后续的一个发展:
采用条件随机场建立类别的关系。
举个简单的例子,"天空"和"鸟"这样的像素在物理空间是相邻的概率,应该要比"天空"和"鱼"这样像素相邻的概率大,那么天空的边缘就更应该判断为鸟而不是鱼(从概率的角度)

