分类/回归/聚类——模型评估

1. 基本概念

模型在训练集上的误差通常称为 训练误差 或 经验误差，而在新样本上的误差称为 泛化误差。显然，机器学习的目的是得到泛化误差小的学习器。然而，在实际应用中，新样本是未知的，所以只能使训练误差尽量小。
在模型评估过程中，分类问题、排序问题、回归问题往往需要使用不同的指标进行评估。在诸多的评估指标中，大部分指标只能片面地反映模型的一部分性能。如果不能合理地运用评估指标，不仅不能发现模型本身的问题，而且会得出错误的结论。

2. 分类模型评估

2.1 混淆矩阵

误差矩阵	预测正值	预测负值
真实正值	TP	FN
真实负值	FP	TN

True Positive(真正, TP)：将正类预测为正类数。
True Negative(真负 , TN)：将负类预测为负类数。
False Positive(假正, FP)：将负类预测为正类数。–> 误报(Type I error)：假的正样本（实际是负样本）。
False Negative(假负 , FN)：将正类预测为负类数。–> 漏报(Type II error)：假的负样本（实际是正样本）。

2.2 准确率（Accuracy）

准确率是指分类正确的样本占总样本个数的比例。
$$ACC=\frac{TP+TN}{TP+TN+FP+FN}$$
准确率是分类问题中最简单也是最直观的评价指标，但存在明显的缺陷。比如，当负样本占99%时，分类器把所有样本都预测为负样本也可以获得99%的准确率。所以，当不同类别的样本占比十分不平衡时，占比较大的样本对准确率影响较大。

2.3 精确率（Precision）

精确率是指分类正确的正样本个数占分类器判定（预测值）为正样本的样本个数的比例，又叫查准率。
$$P=\frac{TP}{TP+FP}$$
TP+FP代表无论真与假，报出来(预测值)数据都是正样本。

医学模型判断癌症病人我们希望Recall高一点（无病诊断为有病去治疗总比漏掉癌症病人好(所有真实患病的人里，检测出患病)），而自己买西瓜的话希望甜瓜的Precision高一点（我们买到的是预测为1(甜瓜)的样本，希望有限的买瓜次数下甜瓜更多）。

2.4 召回率（Recall）

召回率是指分类正确的正样本个数占真正的正样本个数的比例，又叫查全率。
$$R=\frac{TP}{TP+FN}$$

precision与recall小例子:
金融诈骗分类中，正样本P代表是金融诈骗；负样本N代表不是金融诈骗。假设正样本P有100个，负样本N有100个。取threshold=0.5得TP=80，FP=20，问precision和recall分别是多少？如果取threshold=0.9，precision和recall将有什么变化？
解：
$Precision=TP/(TP+FP)=0.8$,也可算误报率0.2，1-0.2 =0.8；
$Recall=TP/(TP+FN)=0.8$,也可计算漏报率0.2，1-0.2=0.8；
若threshold=0.9，则TP减小，TP+FP减小，precision不确定；极端情况下FP为0，precision会上升。TP+FN不变，因此recall会减小。
通过上面的例子我们发现：实际上precision和recall没什么关系。

2.5 P-R（Precision-Recall）曲线

不同情况下我们希望在查准和查全上有个权衡。
因为我们二分类器输出的是预测为正样本的概率，是个[0,1]范围内的数值。那我们可以选择不同的阈值（比如我们的模型预测癌症的概率是0.2, 但是我们为了保守起见，高于0.1就认为是预测的正例）。
P-R曲线的横轴是召回率，纵轴是精确率。
改变阈值就能获得一系列的pair并绘制出曲线。对于不同的模型在相同数据集上的预测效果，我们可以画出一系列的PR曲线。一般来说如果一个曲线完全“包围”另一个曲线，我们可以认为该模型的分类效果要好于对比模型。

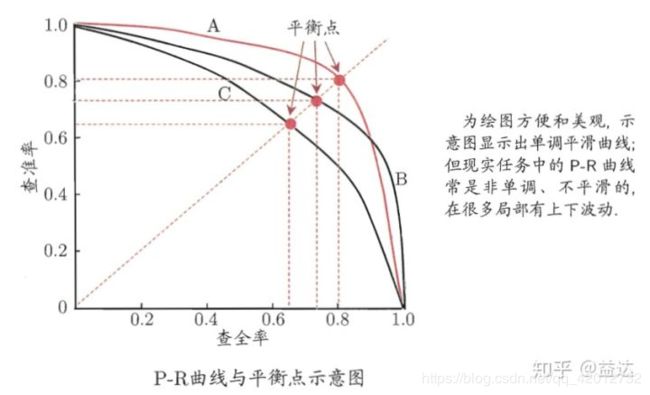
PR曲线越靠近右上越好。

2.6 F1 Score

F1值就是精准率和召回率的调和平均值的2倍。
$$F1=\frac{2\times Precision\times Recall}{Precision+Recall}$$
$$\frac{2}{F_1}=\frac{1}{P}+\frac{1}{R}$$
$$F_1=\frac{2TP}{2TP+FP+FN}$$

上述 $F1$ 值只是在二分类中，我们可以轻易扩展到多分类中。多分类中我们可以使用OneVsRest的策略，判断第i类的分类时，把不属于第i类的看做另一类，就能对每一类都算出一个F值了。使用宏平均（Macro）或者微平均（Micro）来考量多分类的效果。宏平均是多个分类F1值相加，而微平均是多个F1分子分母分别相加。

2.7 ROC曲线

ROC曲线的全称是“受试者曲线”，与PR曲线类似。它相比PR曲线能够在样本不均衡的条件下给出更加合理的结果。先看一下ROC的纵轴和横轴：纵轴是真阳性率（True Positive Rate，TPR），横轴是假阳性率（False Positive Rate，FPR），对应的计算方式是：
$$TPR=\frac{TP}{TP+FN}$$
$$FPR=\frac{FP}{FP+TN}$$
TPR就是召回率（分母为正样本），FPR（分母为负样本）是负样本角度的召回率，即误召率(召回的是负样本的概率)。与PR曲线一样，我们可以通过调整阈值，来改变TPR和FPR。
AUC指的是ROC曲线下的面积大小，该值能够量化地反映基于ROC曲线衡量出的模型性能。计算AUC值只需要沿着ROC横轴做积分就可以了。由于ROC曲线一般都处于y=x这条直线的上方（如果不是的话，只要把模型预测的概率反转成1−p就可以得到一个更好的分类器），所以AUC的取值一般在0.5～1之间。AUC越大，说明分类器越可能把真正的正样本排在前面，分类性能越好。

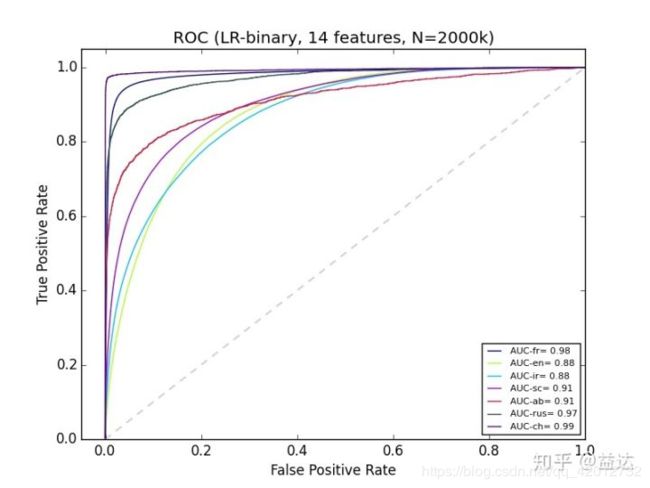
ROC曲线越靠近左上越好。 如果一个模型ROC曲线完全cover另一个，说明该模型优于另一模型。

2.8 AUC(area-under-curve)

AUC一般指的是ROC曲线与横轴构成的面积。
计算方法:

1. 近似法
   
   
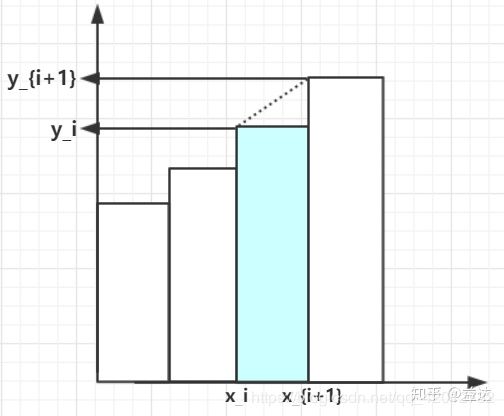
   显然这是个近似的方法，因为我们会多算虚线处三角形面积的一半。并且我们需要改变阈值并绘制出所有的矩形，计算复杂，故这种方法不推荐。
2. 曼 - 惠特尼法
   
   我们构造M*N个正负样本对。然后看看正例样本的predict值大于负例样本的情况，即$P_p>P_n$，计数为1. 如果predict概率相等则需要乘以0.5
   
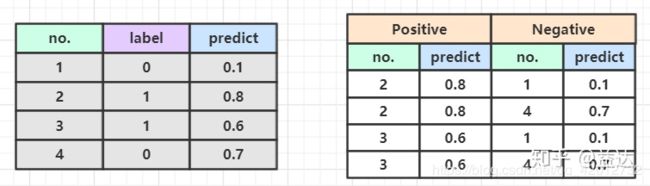
   如上图，我们有4个样本，2正例2负例（M=2，N=2），模型分别输出不同的predict概率。然后我们像上图右侧一样构建正负样本对。所以按照方法2，我们计算出最终的auc为3/4.
3. 排序法
   
   这种属于上面“曼 - 惠特尼法”的优化版本，通过排序避免了 O(MN) 时间的正负样本对构造。我们先看一下怎么算。将数据按照predict从小到大排列，然后得到一个rank。然后计算正样本所在的rank的总和（如下图，总和为2+4=6），然后要减去M(M+1)/2 . 这一个公式可以这样理解：我们取排在第i位的正样本，那它可以构成多少符合条件的 $P_p>P_n$ 样本对呢？
   
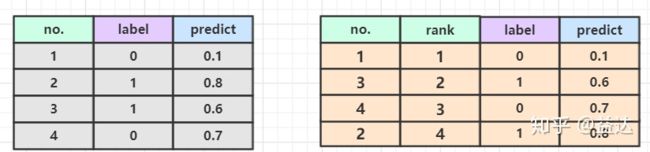
   构成样本对的思路可以这样想：第1正样本，如果它排在 $i_1$ 的位置，那它前面一定有$i_1-1$个负样本；第2个正样本，它排在 $i_2$ 的位置，那它前面一定有$i_2-1-1=i_2-2$ 个负样本（额外的-1是因为前面已经有个正样本了我们不做计算），以此类推我们可以得到递推公式， ${\sum }_{i\in positive}Ran{k}_i-{\sum }_{i=1}^{m}i$ 我们发现这个式子和上面式子的分子是等价的。
   
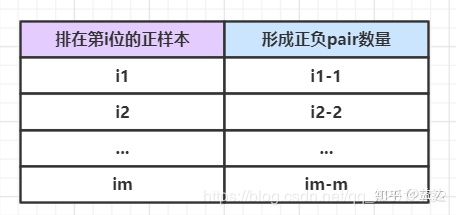
   这样一来，通过排序我们将算法复杂度从 O(MN) 降低到了O(log(M+N)) ，并且经过上面的证明它们是等价的。
   转自：https://zhuanlan.zhihu.com/p/78182116

3. 回归模型评估

3.1 均方误差（MSE）

$$\frac{1}{m}\sum _{i=1}^m(\widehat{y_i}-y_i{)}^2$$
这也是线性回归的损失函数。

3.2 均方根误差（RMSE）

$$\sqrt{\frac{1}{m}\sum _{i=1}^m(\widehat{y_i}-y_i{)}^2}$$
MSE开个根号。数据太大可以开根号。
RMSE能够很好地反映回归模型预测值与真实值的偏离程度。但在实际问题中，如果存在个别偏离程度非常大的离群点（Outlier）时，即使离群点数量非常少，也会让RMSE指标变得很差。
模型在95%的时间区间内的预测误差都小于1%，取得了相当不错的预测结果。那么，造成RMSE指标居高不下的最可能的原因是什么？–离群点。
解决办法？可以从三个角度来思考。
第一，如果我们认定这些离群点是“噪声点”的话，就需要在数据预处理的阶段把这些噪声点过滤掉。
第二，如果不认为这些离群点是“噪声点”的话，就需要进一步提高模型的预测能力，将离群点产生的机制建模进去（这是一个宏大的话题，这里就不展开讨论了）。
第三，可以找一个更合适的指标来评估该模型。关于评估指标，其实是存在比RMSE的鲁棒性更好的指标，比如平均绝对百分比误差（Mean Absolute Percent Error，MAPE），MAPE相当于把每个点的误差进行了归一化，降低了个别离群点带来的绝对误差的影响。

3.3 平均绝对百分比误差（MAPE）

$$MAPE=\frac{100\%}{n}\sum _{i=1}^n|\frac{y_i-\overline{y_i}}{y_i}|$$
范围[0,+∞)，MAPE 为0%表示完美模型，MAPE 大于 100 %则表示劣质模型。
可以看到，MAPE跟MAE很像，就是多了个分母。
注意点：当真实值有数据等于0时，存在分母0除问题，该公式不可用！

3.4 平均绝对误差（MAE）

Mean Absolute Error ，是绝对误差的平均值，能更好地反映预测值误差的实际情况.
$$\frac{1}{m}\sum _{i=1}^m|\widehat{y_i}-y_i|$$

3.5 对称平均绝对百分比误差（SMAPE）

Symmetric Mean Absolute Percentage Error

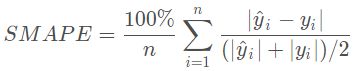
注意点：当真实值有数据等于0，而预测值也等于0时，存在分母0除问题，该公式不可用！

3.6 可决系数（R-Squared）

$$R^2=1-\frac{{\sum }_{i=1}(\widehat{y_i}-y_i{)}^2}{{\sum }_{i=1}(\overline{y_i}-y_i{)}^2}$$
其中，$\widehat{y_i}$是预测值，$\overline{y_i}$是真实值的平均值。$0<=R^2<=1$且越大越好。
三个 sum of squares：

• 总体离差平方和(Total sum of squares) $S{S}_{tot}$ ，它描述的是所有观测点 y 的波动程度:
  $$S{S}_{tot}=\sum _{i=1}^n(y_i-\bar{y}{)}^2$$
• 回归平方和(Explained sum of squares) $S{S}_{reg}$，它是回归模型能够解释的观测点的波动大小：
  $$S{S}_{reg}=\sum _{i=1}^n(\widehat{y_i}-\bar{y}{)}^2$$
• 残差平方和(Residual sum of squares) $S{S}_{res}$ ，是残差的波动大小：
  $$S{S}_{res}=\sum _{i=1}^n(y_i-\widehat{y_i}{)}^2$$
  $$S{S}_{tot}=S{S}_{res}+S{S}_{reg}$$
  $$R^2=1-\frac{S{S}_{res}}{S{S}_{tot}}=\frac{S{S}_{reg}}{S{S}_{tot}}$$
  可决系数反应了线性回归模型能够解释的离差占总离差的比例，即模型的好坏。
  在一元回归中$R^2=r^2$，其中$R^2$为可决系数，r为相关系数。
  在多元回归中，可决系数称为多重可决系数(Maltiple Coefficient of Determination)。

3.7 修正的可决系数（Adjusted R-Squared）

在多元回归中，当样本容量一定时，随着特征的增加可决系数R2总是上升的，即使新特征与因变量不相关，R2也是上升。所以研究人员通常使用修正的可决系数(adjusted R2)$R_a^2$。其定义如下：
$$\begin{array}{rl}{R}_a^2& =1-(1-R^2)\frac{n-1}{n-p-1}\\ & =1-\frac{S{S}_{res}/(n-p-1)}{S{S}_{tot}/(n-1)}\\ & =1-\frac{S{S}_{res}/d{f}_{res}}{S{S}_{tot}/d{f}_{tot}}\end{array}$$
样本量为n， 特征(自变量)数量为p， $S{S}_{tot}$的自由度(degrees of freedom)为 $S{S}_{tot}=n-1$， $S{S}_{res}$的自由度为$d{f}_{res}=n-p-1$。

修正的可决系数$R_a^2\le R^2$。
可能是负数，当样本量较少，特征数量较多时可能会出现负值。

4. 聚类模型评估

a. 外部法（基于有标注）：Jaccard系数、纯度
b. 内部法（无标注）：内平方和WSS和外平方和BSS
c. 此外还要考虑到算法的时间空间复杂度、聚类稳定性等

4.1 外部指标：将聚类结果与某个“参考模型”进行比较

数据集$D=\{x_1,x_2,..,x_m\}$，假定通过聚类给出的簇划分为$C=\{C_1,C_2,..,C_k\}$，参考模型给出的划分簇$C^{\ast }=\{C_1^{\ast },C_2^{\ast },..,C_s^{\ast }\}$，令$\lambda ,{\lambda }^{\ast }$分别表示$C,C^{\ast }$对应簇的标记向量。我们将样本两两配对考虑。
$$a=|SS|,SS=(x_i,x_j)|{\lambda }_i={\lambda }_j,{\lambda }_i^{\ast }={\lambda }_j^{\ast },i<j$$
$$b=|SD|,SD=(x_i,x_j)|{\lambda }_i={\lambda }_j,{\lambda }_i^{\ast }\ne {\lambda }_j^{\ast },i<j$$
$$c=|DS|,DS=(x_i,x_j)|{\lambda }_i\ne {\lambda }_j,{\lambda }_i^{\ast }={\lambda }_j^{\ast },i<j$$
$$d=|DD|,DD=(x_i,x_j)|{\lambda }_i\ne {\lambda }_j,{\lambda }_i^{\ast }\ne {\lambda }_j^{\ast },i<j$$
SS表示包含了在C中隶属于相同簇且在$C^{\ast }$中也隶属于相同簇的样本对。
SD表示包含了在C中隶属于相同簇且在$C^{\ast }$中也隶属于不同簇的样本对。
…以此类推
$$a+b+c+d=m(m-1)/2$$

4.1.1 Jaccard系数

$$JC=\frac{a}{a+b+c}$$

4.1.2 FM指数

$$FM=\sqrt{\frac{a}{a+b}\cdot \frac{a}{a+c}}$$

4.1.3 Rand指数

$$RI=\frac{2(a+d)}{m(m-1)}$$
RI取值范围为[0,1]，值越大意味着聚类结果与真实情况越吻合。
RI越大表示聚类效果准确性越高，同时每个类内的纯度越高。

4.1.4 纯度Purity

$$Purity(\Omega ,C)=\frac{1}{N}\sum _k\underset{j}{\max }|w_k\cap c_j|$$
N表示样本总数，$\Omega =\{w_1,..,w_K\}$ 聚类簇划分。$C=\{c_1,..,c_J\}$真实类标。上述过程即给每个「聚类簇」分配一个「类别」,且「为这个类别的样本」在该簇中「出现的次数最多」,然后计算所有 K 个聚类簇的这个次数之和再归一化即为最终值。
上诉性能度量在[0,1]，越大越好。

4.1.5 NMI标准互信息

Normalized Mutual Information，需要一直真实label。
先介绍互信息MI：
$$MI(U,V)=\sum _{i=1}^R\sum _{j=1}^C{p}_{i,j}log(\frac{p_{i,j}}{p_i\times p_j})$$
其中，$U$代表真实类标集合，$V$代表聚类结果集合。
例如:
对于真实类标集合 $[1,1,2,2]$，聚类类标集合$[1,1,1,2]$
此时$R=2$，$U_i$是index的集合，$U_1=1,2$，$U_2=3,4$
此时$C=2$，$V_j$是index的集合，$V_1=1,2,3$，$V_2=4$
$p_i=\frac{|U_i|}{N}$,$p_j=\frac{|V_j|}{N}$,$p_{i,j}=\frac{|U_i\cap V_j|}{N}$
标准化互信息:
$$NMI(U,V)=\frac{MI(U,V)}{f(H(U),H(V))}$$
其中$H$函数为信息熵，$H(U)=-{\sum }_{i=1}^R{p}_{i}log{p}_i$
$f$可以为$min/max$函数；或几何平均$f(x_i,x_j)=\sqrt{x_i{x}_j}$；或算数平均$f(x_i,x_j)=\frac{x_i+x_j}{2}$

4.2 内部指标：直接考察聚类结果而不利用任何参考模型

考虑聚类结果的簇划分$C=\{C_1,C_2,...,C_k\}$
$avg(C)$对应簇C内样本间的平均距离：$$avg(C)=\frac{2}{|C|(|C|-1)}\sum _{1\le i<j\le |C|}dist(x_i,x_j)$$
$diam(C)$对应簇C内样本间的最远距离：$$diam(C)=ma{x}_{1\le i<j\le |C|}dist(x_i,x_j)$$
$dmin(C_i,C_j)$对应簇$C_i,C_j$间最近样本间距离：$$dmin(C_i,C_j)=mi{n}_{x_i\in C_i,x_j\in C_j}dist(x_i,x_j)$$
$dcen(C_i,C_j)$对应簇$C_i.C_j$中心点的距离：$$dcen(C_i,C_j)=dist({\mu }_i,{\mu }_j)$$

4.2.1 DB指数，值越小越好

Davies-Bouldin Index(戴维森堡丁指数)(分类适确性指标)
$$DBI=\frac{1}{k}\sum _{i=1}^k\underset{j\ne i}{\max }(\frac{avg(C_i)+avg(C_j)}{dcen(C_i,C_j)})$$
含义：类内距离越小，同时类间（簇中心点）距离越大
缺点：因使用欧式距离 所以对于环状分布 聚类评测很差

4.2.2 DV指数,值越大越好

Dunn Validity Index (邓恩指数)
$$DI=\underset{1\le j\le k}{\min }\{\underset{j\ne i}{\min }(\frac{dmin(C_i,C_j)}{{\max }_{1\le l\le k}diam(C_l)})\}$$
任意两个簇元素的最短距离(类间)除以任意簇中的最大距离(类内)
含义：DVI越大意味着类间距离越大，同时类内距离越小
缺点：对离散点的聚类测评很高、对环状分布测评效果差

5. 面试题

5.1 Roc曲线与P-R曲线有何不同？

• 相比P-R曲线，ROC曲线有一个特点，当正负样本的分布发生变化时，ROC曲线的形状能够基本保持不变（稳定），而P-R曲线的形状一般会发生较剧烈的变化（敏感）。ROC曲线在样本不平衡数据集的结果比PR曲线更合理。
• 选择P-R曲线还是ROC曲线是因实际问题而异的，如果研究者希望更多地看到模型在特定数据集上的表现，P-R曲线则能够更直观地反映其性能。

5.2 $R^2$不能完全反映模型预测能力的高低

有很多不同的因素会导致$R^2$值偏高或偏低。仅凭R-Squared的值得出结论模型是好是坏就变得很危险 。例如：

• 当您的预测值是categorical 变量（例如，rating scales或计数时），R平方通常会低于真实数字数据。
• 数据中的真实噪声越多，$R^2$越低。例如，如果根据人们的喜好建立模型，则会产生很多噪音，因此很难实现较高的R平方 。相比之下，天文学现象的模型则相反。
• 当您有更多观察值时，R平方会降低。
• 预测值越多，则R平方 变得更高。
• 如果您的数据不是简单的随机样本，则可以对R平方 进行夸大。例如，考虑基于时间序列数据或地理数据的模型。这些很少是简单的随机样本，并且往往会获得更高的R平方 统计量。
• 当您的模型不包括重要特征时，R平方 将必定很小。例如，如果您有一个模型来研究品牌形象如何驱动品牌偏好，而您的模型却忽略了诸如价格，分销，风味和质量等实际情况，那么即使您的模型很棒，R-Squared也不可避免地会变小。
• 基于聚合数据（例如，状态级别数据）的模型比基于案例级别数据的模型具有更高的R平方 统计量。
  https://www.displayr.com/8-tips-for-interpreting-r-squared/

不能用$R^2$值高低来比较不同模型的好坏？

• 在很多情况下，$R^2$值会产生误导。例如比较基于aggregate数据/disaggregate数据的模型时，或者变量被transformed的模型
• 其他更好的指标，F-Tests, Bayes’ Factors, Information Criteria, and out-of-sample predictive accuracy.