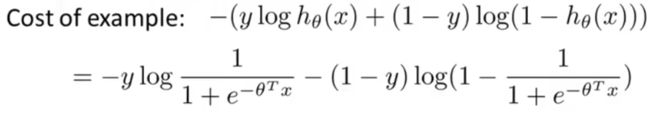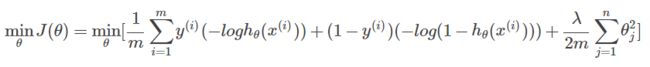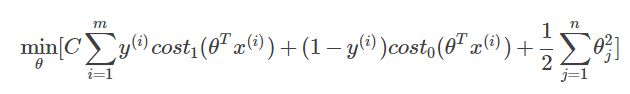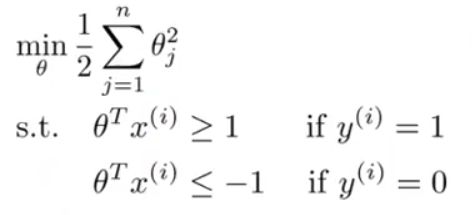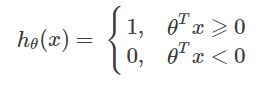Coursera 机器学习(by Andrew Ng)课程学习笔记 Week 7——支持向量机
此系列为 Coursera 网站机器学习课程个人学习笔记(仅供参考)
课程网址:https://www.coursera.org/learn/machine-learning
参考资料:http://blog.csdn.net/scut_arucee/article/details/50419229
一、支持向量机的引入
1.1 从逻辑回归引入SVM
支持向量机(Support Vector Machine,SVM)是一个广泛应于在工业界和学术界的分类算法。与逻辑回归和神经网络相比,它在学习非线性复杂方程上提供了一种更加清晰、更加有效的思路。这一部分我们就来介绍这一算法。
为了描述支持向量机,我们会先从逻辑回归开始讲起,再一点一点修正得到最后的支持向量机。
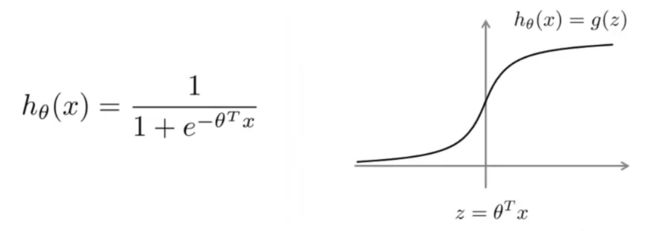
在逻辑回归中,我们已经熟悉了如下所示的假设函数 hθ(x) 和逻辑函数曲线:
在逻辑回归中,如果 y=1 ,我们希望 hθ(x)≈1 ,即 θTx≫0 ;如果 y=0 ,我们则希望 hθ(x)≈0 ,即 θTx≪0 。
逻辑回归中,单个样本(x,y)代价为:
我们对上面的式子分两种情况进行分析:
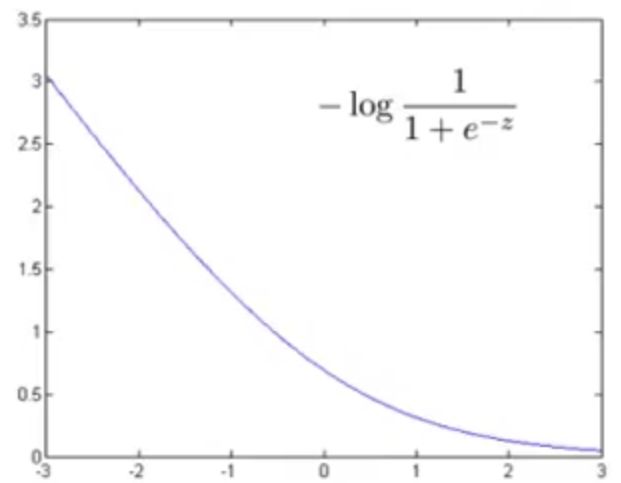
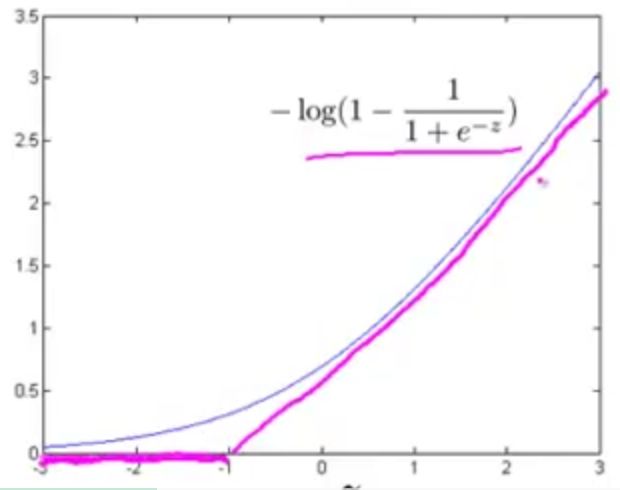
① 如果 y=1 ,上式中只有第一项起作用,第二项为 0 。此时,画出函数图像:
结合此图也可以看出对于正样本(即 y=1 ),为了使代价 −log11+e−z 最小,我们将尽可能将 z=θTx 设置得比较大,此时代价接近于 0 。
在支持向量机中这种情况可以用两条线段作为新的代价函数 cost1(z) ,如下图桃红色部分:
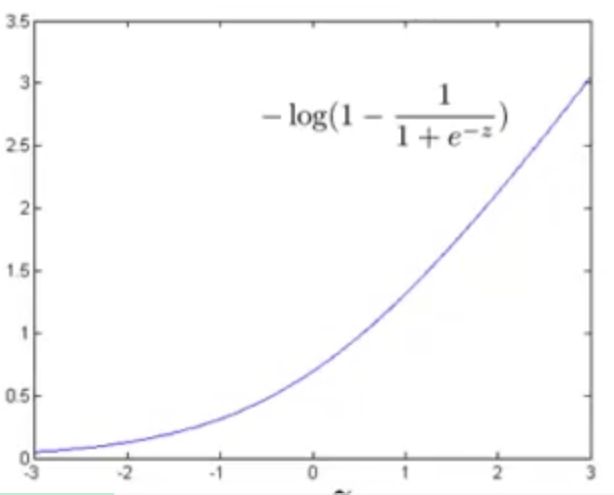
② 如果 y=0 ,上式中只有第二项起作用,第一项为 0 ,此时代价随 z 的变化曲线如下图所示:
此时,我们也可以用两条线段代替如上曲线,作为新的代价函数 cost0(z) ,如下图桃红色部分:
我们接下来就通过 cost1(z) 、 cost0(z) 构建支持向量机。
1.2 SVM的优化目标
对于逻辑回归,优化目标为:
可能看起来与以前的式子稍有不同,是因为我们将负号移到了括号里面。
接下来我们将 cost1(z) 、 cost0(z) 替换进去:
由于无论是否有 1m 都不会影响最小化的结果,在使用支持向量机时,我们常常忽略 1m 。
对于逻辑回归正则化代价函数,我们可以用 A+λB 来表示,其中 A 表示训练样本的代价, B 表示正则化项,通过设置 λ 的值来控制 A 和 B 之间的平衡 ,使拟合效果更好。
而支持向量机则采用另一个参数 C 来控制 A 和 B 之间的平衡,优化目标为: CA+B 。
所以,支持向量机(SVM)的优化目标为:
二、最大间距分类器
2.1 SVM的决策边界
有时,人们会将支持向量机称为最大间距分类器,这一部分会给大家解释其中原因,这样我们对SVM的假设得到一个更直观的理解。
上面的式子是SVM的优化目标(代价函数),中间左图是 cost1(z) 的图像,右侧是 cost1(z) 的图像。
我们来看怎样使得上面的代价函数最小:
① 对于一个正样本( y=1 ),要使 cost1(z)=0 ,我们希望 z=θTx⩾1 。
② 对于一个负样本( y=0 ),要使 cost0(z)=0 ,我们希望 z=θTx<−1 。
接下来,我们考虑一个特例:
如果 C 设置的非常大,例如: 100000 ,在最小化优化目标的过程中,我们会希望找到一个能够使 A=0 (中括号部分)的最优解。这就要求当 y=1 , θTx⩾1 ;当 y=0 , θTx<−1 。
现在再来考虑我们的优化问题,我们可以选择一个参数使得 A=0 ,SVM的优化目标就转化为:
SVM的这个要求会对决策边界有什么影响呢?
以一个线性可分数据集为例,有多条直线可以把正样本与负样本分开,如下图:
SVM会趋于以黑色决策边界来分离正、负样本,因为黑色线与训练样本之间有更大的最短距离,在分离正负样本上的表现会更好。而粉色线和绿色线离样本比较近,在分离样本时表现就会比较差。SVM总是努力用最大间距(margin)来分离样本,这也是它为什么被称为大间距分类器,同时这也是SVM具有鲁棒性的原因。
事实上,SVM比大间距分类器表现得更成熟,比如异常点的影响,如图:
参数 C 控制着对误分类的训练样本的惩罚,当我们将参数 C 设置的较大时,优化过程会努力使所有训练数据被正确分类,这会导致仅仅因为一个异常点决策边界就能从黑色线变成粉色线,这是不明智的。SVM可以通过将参数 C 设置得不太大而忽略掉一些异常的影响,这样以来,对于这个例子,我们仍然会得到黑线代表的决策边界。即使训练样本不是如上图那样线性可分,SVM也能将它们恰当地分开。这里, C 的作用类似于 1λ 。
2.2 SVM背后的数学原理
这一部分内容涉及到向量内积部分的知识,可以自行复习一下。
这是我们之前提到的SVM的优化目标:
为了简化,方便下面画示意图,令 θ0=0 ,特征数 n=2 ,那么上面的式子就可以改写为:
其中, ∥θ∥ 为向量 θ 的长度或称为 θ 的范数。
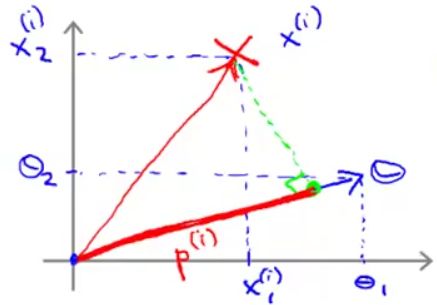
如果将 θTx(i) 看成是经过原点的两个向量相乘,如下图:
则 θTx(i) 等价于向量 x(i) 在向量 θ 上的投影 p(i) 与 θ 的范数 ∥θ∥ 相乘,即:
故SVM的优化目标就变为:
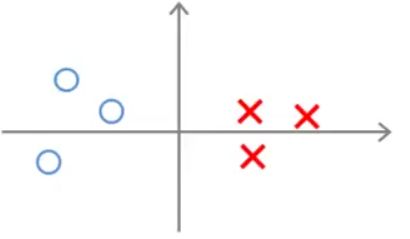
我们来看对于下面的数据集,SVM会选择哪种决策边界(假设 θ0=0 )。
① 小间距决策边界
如图,绿色直线为决策边界,这个决策边界离样本的距离很近。根据前面所说,SVM不会选择小间距决策边界,我们来看看为什么。
由于 θ0=0 ,所以向量 θ 过原点,又知道,向量 θ 的斜率为 θ2θ1 ,决策边界为 θTx=0 ,即 θ1x+θ2x=0 ,斜率为 −θ1θ2 ,也就是说向量 θ 过原点且与决策边界垂直(如上图蓝色直线所示)。,
取上图中最贴近决策边界的一个正样本(红叉)点 x(1) ,因为正样本点 y(1)=1 ,故要求 p(1)∥θ∥⩾1 。但事实是这种小间距决策边界, x(1) 在向量 θ 上的投影 p(1) 非常小,这就要求 ∥θ∥ 很大,显然这与优化目标 minθ12∑nj=1θ2j=minθ12∥θ∥2 不符。
同理,上图中最贴近决策边界的一个负样本(蓝圈)点 x(2) ,因为负样本点 y(2)=0 ,故要求 p(1)∥θ∥⩽−1 。 x(2) 在向量 θ 上的投影 p(2)<0 且 |p(2)| 也非常小,这也要求 ∥θ∥ 很大。
由于这种小间距决策边界的选择与SVM的优化目标不符,故SVM不会选择这种决策边界。
② 大间距决策边界
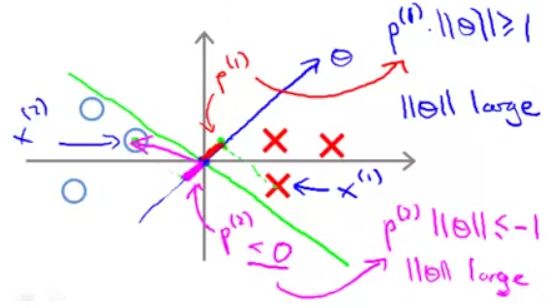
如果选用下图绿色线作为决策边界:
同样的,决策边界也是和向量 θ 垂直的。不同的是,对于正样本点 x(1) ,它在 θ 上的投影 p(1) 比小间距分类那里的要长多了;对于负样本点 x(2) ,它在 θ 上的投影 p(2) 的长度比小间距分类那里也要长很多。在满足SVM优化目标的要求时, ∥θ∥ 可以变小而不必很大。
反过来看,通过在优化目标里让 ∥θ∥ 不断变小,SVM就可以选择出上图所示的大间距决策边界。这也是SVM可以产生大间距分类器的原因。
以上我们都是假设 θ0=0 ,这会让决策边界通过原点,幸运的是即使 θ0≠0 ,SVM会产生大间距分类仍然是成立的,但这里我们不做证明。
三、核函数(Kernels)
SVM利用核函数可以构造出复杂的非线性分类器。如下图:
3.1 SVM的假设函数
注意这里是假设函数, θTx⩾0,hθ(x)=1 ,而前面的 θTx⩾1,, if y=1 是优化目标,不要搞混。
3.2 非线性决策边界特征变量的定义
例如假设函数:
f 为定义的特征变量,我们可以定义特征项 f1=x1,f2=x2,f3=x1x2,f4=x21,⋯ 。
之前在多项式回归中也提到,加入这些高阶项,我们可以得到更多的特征变量,但是我们并不知道这些高阶项是否是我们真正想要的,在计算机视觉中,输入是很多像素,如果用这些高阶项作为特征变量,运算量将会变得非常大。那么,对于SVM,有没有比这些高阶项更好的特征项?
3.3 高斯核函数
给定 x ,我们可以提前手动选取一些标记点,然后根据与这些标记点的接近程度来计算新的特征项。如下图手动选择了3个标记点 l(1),l(2),l(3) ,如下图:
定义:
这种相似度,用数学术语来说,就是核函数(Kernels)。核函数有不同的种类,其中常用的就是我们上述这种高斯核函数。
我们可以将上式改写为:
如果 x 的位置接近于 l(1) ,即 x≈l(1) ,则:
相反,如果 x 的位置远离于 l(1) ,则:
我们之前定义了三个标记点 l(1),l(2),l(3) ,从每个标记点可以根据上面的式子定义一个新的特征变量,也就是说,给定一个样本 x ,我们可以计算出三个特征变量 f1,f2,f3 。
我们假设现在有两个特征, x1 和 x2 ,第一个标记点 l(1)=[35] ,我们设置不同的 σ 的值并画出 f1 的图像:
中间一行为 f1 的3D图,纵轴高度为 f1 ,水平两个轴分别为 x1 和 x2 ,下面一行为对应的等高线图。
当 x=[35] 时,即 x=l(1) , f1=1 位于最高点。而当 x 远离 [35] 时,如下图的边缘位置,则 f1≈0 。
f 的值在 0 与 1 之间,具体取决于 x 与标记点 l 的接近程度。
第一列为 σ2=1 的情况,观察上图我们可以发现,当改变核函数中 σ2 的大小,如减小到 σ2=0.5 ,可看到突起变窄了,等高线图也收缩了,说明从 1 降到低处的速度变得更快,同样的,如果增大 σ2 的值,例如 σ2=3 ,则突起会变宽,新的特征值从大减小的速度会变慢。
3.4 通过核函数和标记点构造复杂的非线性边界
假设只考虑3个标记点,根据SVM假设函数的定义,若 θ0+θ1f1+θ2f2+θ3f3⩾0 ,则预测 y=1 。
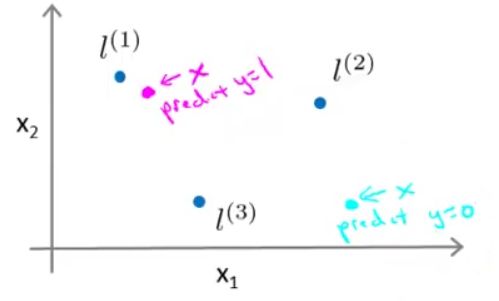
假设我们已经得到 θ0=−0.5,θ1=1,θ2=1,θ3=0 ,标记点和训练样本的位置如下图:
对于粉色样本点,根据前面定义的新特征项的图像, f1≈1,f2≈0,f2≈0 ,所以, θ0+θ1f1+θ2f2+θ3f3=0.5>0 ,预测 y=1 。
对于蓝绿色样本点,根据前面定义的新特征项的图像, f1≈0,f2≈0,f2≈0 ,所以, θ0+θ1f1+θ2f2+θ3f3=−0.5<0 ,预测 y=0 。
综上可以发现,对于接近标记点 l(1) 或 l(1) 的点,预测结果为 y=1 ,而对于那些远离标记点 l(1) 和 l(2) 的点,预测结果为 y=0 。
故,最终的决策边界会是非线性的,在边界内部预测 y=1 ,在边界外部预测 y=0 ,如下图:
3.5 标记点的选择及特征向量的构造
在实际应用中,如何选择这些标记点 l(1),l(2),l(3),⋯ 是机器学习必须解决的问题。
给定 m 个训练样本 (x(1),y(1)),(x(2),y(2)),(x(3),y(3)),⋯,(x(m),y(m)) ,可以选择 l(1)=x(1),l(2)=x(2),l(3)=x(3),⋯,l(m)=x(m) ,即选择与样本点重合的位置作为标记点。
给定一个样本x(可属于训练集,交叉验证集或测试集),则:
还可添加一个额外的特征 f0=1 ,得到特征向量:
假设有一个训练样本 (x(i),y(i)) ,可以得到它的特征向量:
四、SVM总结
4.1 假设函数及优化目标
在实现中,最后一项 12∑mj=1θ2j ( θ0 不进行正则化)不用 θTθ 表示,而是用 θTMθ , M 是一个矩阵,具体取决于核数,这样可以提高运行效率。
4.2 SVM的参数选择
参考上一讲的方差与偏差部分:
前面提到参数 C 相当于逻辑回归中的 1λ ,那么参数 C 对方差和偏差的影响如下:
C 太大,相当于 λ 太小,会产生高方差,低偏差;
C 太小,相当于λ λ 太大,会产生高偏差,低方差。
同时,参数 σ2 也会对方差和偏差产生影响:
σ2 大,则特征 f(i) 变化较缓慢,可能会产生高偏差,低方差;
σ2 小,则特征 f(i) 变化不平滑,可能会产生高方差,低偏差。
4.3 使用SVM
在具体实现时,我们不需要自己编写代码来最优化参数 θ ,而是使用SVM软件包(如:liblinear,libsvm等)来最优化参数 θ 。
当然了,在使用这些软件包时,我们需要自己选择参数 C 以及选择使用哪种核函数。
例如:选用线性核函数(即,没有使用核函数),若 θ0+θ1f1+θ2f2+θ3f3⩾0 ,则 hθ(x)=1 。最终这会产生一个线性分类器。liblinear就是使用线性核函数。
如果特征数 n 很大,而训练样本数 m 很小,使用线性核函数产生一个线性分类器就较为适合,不容易过拟合。
如果特征数 n 很小,而训练样本数 m 很大,就适合用一个核函数去实现一个非线性分类器,高斯核函数是个不错的选择。
如果使用的是高斯核函数: fi=exp(∥∥x−l(i)∥∥22σ2) ,其中 l(i)=x(i) ,则还需要选择参数 σ2 。
在写代码实现高斯核函数时,可以参考下列形式:
核函数还有一些其他选择,需要注意的是,不是所有的相似度函数都是有效的核函数,要成为有效的核函数,需要满足默塞尔定理(Mercer’s Theorem)这个技术条件。
还有一些其他核函数如:多项式核函数,字符串核函数、卡方核函数等等,但大多数时候我们用的还是高斯核函数。
4.4 用SVM解决多类别分类问题
对于 K 类分类问题,可以使用已经内置了多类别分类函数的SVM软件包,也可以用一对多(one-vs-all)的方法训练 K 个SVM分类器,把 y=i(i=1,2,⋯,K) 的类同其他类区别开来,得到 K 个参数向量 θ(1),θ(2),⋯,θ(K) 。
对于输入的 x ,选择 (θ(i))Tx 最大的那个类别 i 作为识别结果。
4.5 SVM和逻辑回归的选择
我们如何选择使用SVM还是逻辑回归来解决分类问题?
①如果特征数 n 相对于训练样本数 m 来说很大:
则应该使用逻辑回归或者线性核函数(无核)的SVM。 m 较小时,使用线性分类器效果就挺不错了,并且也没有足够的数据去拟合出复杂的非线性分类器。
②如果特征数 n 很小,训练样本数 m 中等大小:
则应该使用高斯核函数SVM。
③如果特征数 n 很小,训练样本数 m 很大:则高斯核函数的SVM运行会很慢。这时候应该创建更多的特征变量,然后再使用逻辑回归或者线性核函数(无核)的SVM。
对于以上这些情况,神经网络很可能做得很好,但是训练会比较慢。实际上SVM的优化问题是一种凸优化问题,好的SVM优化软件包总是能找到全局最小值或者是接近全局最小的值。
附课后测试题答案
答案:C
答案:BD
答案:BD