libsvm相关变量总结以及libsvm 参数粗调、微调技巧 和PCA主成分分析princomp函数的使用

libsvm搭建的支持向量机运行起来，在命令行里会蹦出很多变量，开始的时候，我不以为意。现在想想这样糊弄，到最后还是稀里糊涂，不如一次总结，当做日后的复习资料。

运行起来会出现这些：

1.变量总结

     *

optimization finished, #iter = 162

nu = 0.431029

obj = -100.877288, rho = 0.424462

nSV = 132, nBSV = 107

      Total nSV = 132

其中：

#iter为迭代次数

nu是选择的核函数类型的参数

obj为SVM文件转换为的二次规划求解得到的最小值

rho为判决函数的偏置项b

nSV 为标准支持向量个数(0

nBSV为边界上的支持向量个数(a[i]=c)

Total nSV为支持向量总个数（对于两类来说，因为只有一个分类模型Total nSV = nSV，但是对于多类，这个是各个分类模型的nSV之和）。

2.libsvm参数粗调与微调

先给出SVMcgForClass函数的代码（这个函数是《MATLAB神经网络30个案例分析》这本书里面用于对svm，c、g变量进行交叉验证的函数）

function [bestacc,bestc,bestg] = SVMcgForClass(train_label,train,cmin,cmax,gmin,gmax,v,cstep,gstep,accstep)
%SVMcg cross validation by faruto

%
% by faruto
%Email:[email protected] QQ:516667408 http://blog.sina.com.cn/faruto BNU
%last modified 2010.01.17
%Super Moderator @ www.ilovematlab.cn

% 若转载请注明：
% faruto and liyang , LIBSVM-farutoUltimateVersion 
% a toolbox with implements for support vector machines based on libsvm, 2009. 
% Software available at http://www.ilovematlab.cn
% 
% Chih-Chung Chang and Chih-Jen Lin, LIBSVM : a library for
% support vector machines, 2001. Software available at
% http://www.csie.ntu.edu.tw/~cjlin/libsvm

% about the parameters of SVMcg 
if nargin < 10
    accstep = 4.5;
end
if nargin < 8
    cstep = 0.8;
    gstep = 0.8;
end
if nargin < 7
    v = 5;
end
if nargin < 5
    gmax = 8;
    gmin = -8;
end
if nargin < 3
    cmax = 8;
    cmin = -8;
end
% X:c Y:g cg:CVaccuracy
[X,Y] = meshgrid(cmin:cstep:cmax,gmin:gstep:gmax);
[m,n] = size(X);
cg = zeros(m,n);

eps = 10^(-4);

% record acc with different c & g,and find the bestacc with the smallest c
bestc = 1;
bestg = 0.1;
bestacc = 0;
basenum = 2;
for i = 1:m
    for j = 1:n
        cmd = ['-v ',num2str(v),' -c ',num2str( basenum^X(i,j) ),' -g ',num2str( basenum^Y(i,j) )];
        cg(i,j) = svmtrain(train_label, train, cmd);
        
        if cg(i,j) <= 55
            continue;
        end
        
        if cg(i,j) > bestacc
            bestacc = cg(i,j);
            bestc = basenum^X(i,j);
            bestg = basenum^Y(i,j);
        end        
        
        if abs( cg(i,j)-bestacc )<=eps && bestc > basenum^X(i,j) 
            bestacc = cg(i,j);
            bestc = basenum^X(i,j);
            bestg = basenum^Y(i,j);
        end        
        
    end
end
% to draw the acc with different c & g
figure;
[C,h] = contour(X,Y,cg,70:accstep:100);
clabel(C,h,'Color','r');
xlabel('log2c','FontSize',12);
ylabel('log2g','FontSize',12);
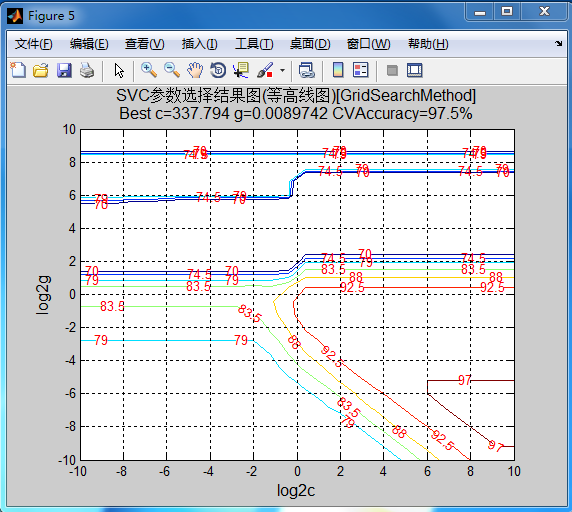
firstline = 'SVC参数选择结果图(等高线图)[GridSearchMethod]'; 
secondline = ['Best c=',num2str(bestc),' g=',num2str(bestg), ...
    ' CVAccuracy=',num2str(bestacc),'%'];
title({firstline;secondline},'Fontsize',12);
grid on; 

figure;
meshc(X,Y,cg);
% mesh(X,Y,cg);
% surf(X,Y,cg);
axis([cmin,cmax,gmin,gmax,30,100]);
xlabel('log2c','FontSize',12);
ylabel('log2g','FontSize',12);
zlabel('Accuracy(%)','FontSize',12);
firstline = 'SVC参数选择结果图(3D视图)[GridSearchMethod]'; 
secondline = ['Best c=',num2str(bestc),' g=',num2str(bestg), ...
    ' CVAccuracy=',num2str(bestacc),'%'];
title({firstline;secondline},'Fontsize',12);

然后应用这个函数对c、g参数进行交叉验证，会得到一个比较粗略的范围，一个是2维的logc,logg的等高图，一个是3维的准确率，logc，logg的图。通过先出的图得到一个比较粗略的c、g范围，然后在这个范围上进一步缩小范围，同时accstep变量是画出图像的步长，通过调节这个值可以方便地将图放大缩小。

3.PCA主成分分析princomp函数的使用

这个函数有一个比较变态的地方就是 行列变换容易把人搞糊涂。

基本形式就是这个了：[COEFF,SCORE,latent,tsquare] = princomp(X)

1、输入参数 X 是一个 n 行 p 列的矩阵。每行代表一个样本观察数据，每列则代表一个属性，或特征。

2、COEFF 就是所需要的特征向量组成的矩阵，是一个 p 行 p 列的矩阵，每列表示一个出成分向量，经常也称为（协方差矩阵的）特征向量。并且是按照对应特征值降序排列的。所以，如果只需要前 k 个主成分向量，可通过：COEFF(:,1:k) 来获得。

3、SCORE 表示原数据在各主成分向量上的投影。但注意：是原数据经过中心化后在主成分向量上的投影（the representation of X in the principal component space.  Rows of SCORE correspond to observations, columns to components.）。即通过：SCORE = x0*COEFF 求得。其中 x0 是中心平移后的 X（注意：是对维度进行中心平移，而非样本。），因此在重建时，就需要加上这个平均值了。

4、latent 是一个列向量，表示特征值，并且按降序排列。（the principal component   variances, i.e., the eigenvalues of the covariance matrix of X）。