2D多人关键点：《Realtime Multi-Person 2D Pose Estimation using Part Affinity Fields》

《Realtime Multi-Person 2D Pose Estimation using Part Affinity Fields》
 来源：CMU，OpenPose开源多人姿态模型
 源码：https://github.com/ZheC/Realtime_Multi-Person_Pose_Estimation

 本文虽然是2016年的论文，但其文中提出的方法还是很值得学习和借鉴的

0 摘要

 本文提出了一种局部关联场（PAF，Part Affinity Fields）方法，来实现自底向上（bottom-up）的多人2D姿态估计；
 PAF：它是一种将单个人的各个局部进行关联；即同一个人的相邻部位关联度强（更具亲和力），如肘部和腕部，不同人之间的部位关联度弱，甚至没有关联，并用一个２D向量场来表示；且将这种关联关系同关键点一起放入到CNN网络进行学习，从而达到端到端的自底向上的多人姿态估计
 在COCO 2016 keypoints challenge多人场景上，大大超越了之前的方法，效率和效果都取得非常大的进步

1介绍

 １）单人场景，略过
 ２）多人场景，难点
  Ａ）每张图像上的人数未知，位置不定，占比不定
  B）人与人之间，相互接触，相互遮挡，部分交叉等增加了关联难度
  C）人数越多，复杂度越大，实时性难保证
 ３）多人场景，自上向下（top-dwon）
  也就是先用目标检测手段，定位每个个体，将问题转化为单人场景；这种方法有2个隐患：
  A）对目标检测要求高，且有时间开销
  B）人数较多时，每个人都需要跑一次前向网络，时间开销太大
 4）多人场景，自底向上（bottom-up）
  类似于本文的方法，CNN网络可能复杂度高，但不会因人数多少增加时间开销，也不用目标检测

 文中对这两种方案进行了时间开销对比，如下图：

2 PAF

2.1 Overall pipeline

 首先，输入$w\ast h$图像Fig. 2a，2D关键点Fig. 2e；
 然后，two-branch CNN：
 1）一路预测身体关键点的2D置信度映射图集S（part confidence map），如Fig. 2b
$$S=(S_1,S_2,...,S_J)，S_j\in {\mathbb{R}}^{w\ast h}$$
  J表示映射图个数，一般为关键点个数+1（背景）
 2）另一路预测局部关联场对2D向量场集L（part affinity vector field），如Fig. 2c
$$L=(L_1,L_2,...,K_C)，S_c\in {\mathbb{R}}^{w\ast h\ast 2}$$
  L用来编码部位之间的关联程度，对于每个肢体（成对的部位）具有C个向量场；每个点编码成一个2D向量场Lc，如图：

  肢体：由关键点对组成，如右肘关节和右腕关节，尽管这里的某些肢体可能不是人的真正肢体；2D向量编码这个肢体的位置和方向
 最后，通过对置信度映射和关联场进行贪婪推理得出所有人的关键点，如Fig. 2d

2.2 Simultaneous Detection and Association

 如上述所说，本文采用two-branch multi-stage CNN作为最终CNN框架；如上图，上半部分为关联场预测网络，下半部分为关键点预测网络，并采用多级（stage）级联方法 ，每级之后，将图像和两个支流融合到一起供下一级使用；且在训练过程中，每级都会进行loss监督（中间监督）
 用数学式表达框架为：

2.3 Loss Function

 loss function：

 其中，t表示第几级，
 $S_j^{\ast }(p)$表示groundtruth part confidence map；
 $L_c^{\ast }(p)$表示groundtruth part affinity vector field；
 W表示二值mask，$W(p)=0$就表示当前点p缺失（不可见或不在图像中），用来避免训练时错误惩罚
 且在训练时，增加中间级监督，防止梯度消失（vanishing gradient problem）
 最终loss为：

2.4 Confidence Maps for Part Detection

 理论上每个confidence map是对应groundtruth位置单个像素响应（为1），其他像素点位0；但在实际应用中，我们是用高斯函数生成对应groundtruth位置，周围像素响应（高斯响应）
 对于单人场景来说，一个响应图只有一个峰值响应；
 而多人场景，就复杂得多了，一个响应图中，每个人k对应可见点j都应该有峰值响应：

 在预测阶段，通过对个体置信度响应进行max操作和非最大化抑制获取候选点：

2.5 Part Affinity Fields for Part Association

  如图：

 1）如上图中Fig. 5a，给定检测到身体的候选点（红色和蓝色点），在人数未知情况下，我们如何确定那些点是同一个人的呢？？？这就是自底向上（bottom-up）多人姿态估计面临的最大挑战
 2）面对这样一个问题，我们就需要一个描述部位（点）之间关系的一种度量，一种表示方法，来判定；
 3）测量关联的一种可能方法是检测肢体上每对点之间的额外中点，并检查候选点之间的关联，如图Fig. 5b所示；然而，当人们聚集在一起时，这些中点很可能支持错误的关联(如图Fig. 5b中的绿线所示)，这种错误的关联是由表示中两个局限引起的:
  (1)它只编码每一肢体的位置，而没有方向；
  (2)将肢体的支撑区域缩小到单点（中点）。
 4）针对一些局限，本文提出了一种新的表示方法，即局部关联场（PAF），它将整个肢体区域作为支撑域，并同时编码位置和方向信息，如图Fig. 5c；对于属于肢体的每个像素，PAF对从肢体的一点到另一点的方向进行编码，每种类型的肢体都有一个2D向量场来表示。

向量场表示

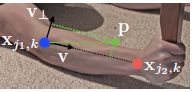
 1）上图表示一个肢体，$x_{j1,k}$，$x_{j2,k}$表示图像种第k个人的肢体c中的两个groundtruth点j1和j2
 2）点p是肢体上的点，当然它有界定范围：

  其中：
  $v=(x_{j2,k}-x_{j1,k})/||x_{j2,k}-x_{j1,k}|{|}_2$表示肢体单位方向向量
  $v_{\perp }$表示v的垂直向量
  $l_{c,k}=||x_{j2,k}-x_{j1,k}|{|}_2$表示肢体长度
  ${\sigma }_l$ 表示肢体宽度
 3）则肢体区域的向量场表示为：

 4）最终向量场groundtruth是平均图像中的所有个人：

  其中$n_c(p)$表示非0点数的平均值
 5）预测阶段，我们计算相应向量场上的线段积分来衡量关联关系；换句话说，我们计算PAF连接候选肢体的线队列，如候选点$d_{j1}$,$d_{j2}$

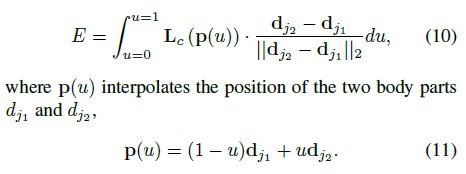
  在实际应用中，我们通过采样和等间距u值的累加来近似积分。

2.6 MultiPerson Parsing using PAFs

 我们对检测置信度映射进行非最大抑制操作，以获取候选点位置的离散集，如图：

 1）对于每个部位，可能有多个候选项，因为图像中有多个人或误报（Fig. 6b），这些候选部位定义来大量可能的分支；
 2）我们使用PAF来对这些分支进行评分，如式10，找到这个最有解问题是一个NP-Hard的K维匹配问题；本文中提出来一种贪婪松弛方法，它可以持续的产生高质量的匹配，这也得益于PAF进行全局上下文编码，拥有很大的接受域
 3）定义$Z_{j_1{j}_2}^{mn}\in \{0,1\}$来表示候选点$d_{j_1}^m$，$d_{j_2}^n$是否连接，从而我们优化目标就变成找到最优匹配，从可能连接中：$$Z=\{z_{j_1{j}_2}^{mn}:for{j}_1,j_2\in \{1,...,j\};m\in \{1,...,N_{j_1}\};n\in \{1,...,N_{j_2}\}\}$$
 4）在这种图匹配问题中，我们目标就是找到最大权重（式10）匹配

3 结果

 关于效果我不打算啰嗦太多，实测看Openpose视频：