一、为什么有CART回归树
以前学过全局回归,顾名思义,就是指全部数据符合某种曲线。比如线性回归,多项式拟合(泰勒)等等。可是这些数学规律多强,硬硬地将全部数据逼近一些特殊的曲线。生活中的数据可是千变万化。那么,局部回归是一种合理地选择。在斯坦福大学NG的公开课中,他也提到局部回归的好处。其中,CART回归树就是局部回归的一种。
二、CART回归树的算法流程

注意到,(1)中两步优化,即选择最优切分变量和切分点。(i)如果给定x的切分点。那么可以马上求得中括号内的最优。(ii)对于切分点怎么确定,这里是用遍历的方法。
三、CART分类树
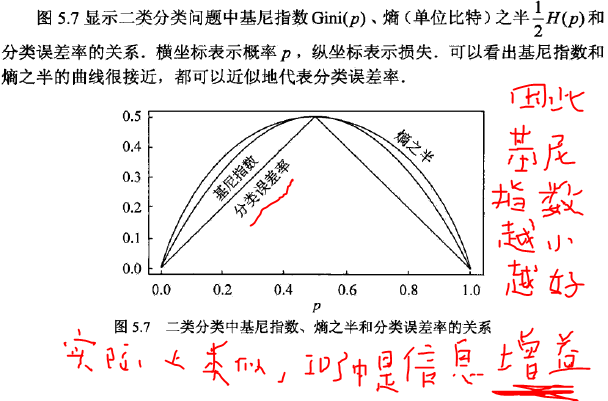
实际上,CART分类树的生成树和ID3方法类似,只是这里用基尼指数代替了信息增益,定义




四、CART剪枝算法流程

例子参考:http://www.cnblogs.com/zhangchaoyang/articles/2709922.html
比如:
当分类回归树划分得太细时,会对噪声数据产生过拟合作用。因此我们要通过剪枝来解决。剪枝又分为前剪枝和后剪枝:前剪枝是指在构造树的过程中就知道哪些节点可以剪掉,于是干脆不对这些节点进行分裂,在N皇后问题和背包问题中用的都是前剪枝,上面的χ2方法也可以认为是一种前剪枝;后剪枝是指构造出完整的决策树之后再来考查哪些子树可以剪掉。
在分类回归树中可以使用的后剪枝方法有多种,比如:代价复杂性剪枝、最小误差剪枝、悲观误差剪枝等等。这里我们只介绍代价复杂性剪枝法。
对于分类回归树中的每一个非叶子节点计算它的表面误差率增益值α。
是子树中包含的叶子节点个数;
是节点t的误差代价,如果该节点被剪枝;
r(t)是节点t的误差率;
p(t)是节点t上的数据占所有数据的比例。
是子树Tt的误差代价,如果该节点不被剪枝。它等于子树Tt上所有叶子节点的误差代价之和。
比如有个非叶子节点t4如图所示: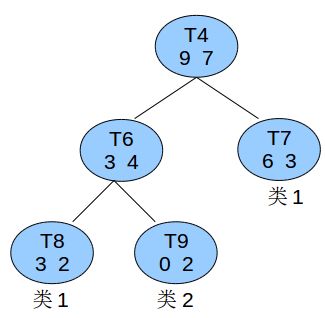
已知所有的数据总共有60条,则节点t4的节点误差代价为:
子树误差代价为:
以t4为根节点的子树上叶子节点有3个,最终:
找到α值最小的非叶子节点,令其左右孩子为NULL。当多个非叶子节点的α值同时达到最小时,取最大的进行剪枝。
#include
#include
#include
#include<string>
#include
参考文献:
http://blog.csdn.net/google19890102/article/details/32329823







