这篇博客是基于本人在美国堪萨斯大学的Introducion to machine learning的课件资料和课程笔记,进行整理与总结,也包含自己在做课程project过程中的经验
1.简介
机器学习有很多算法,有很多注意点都是相似的,拿最成熟和应用最广的分类(classification)来说。对于一个分类器(classifier), 输入值一般是包含离散或者是连续值特征值(feature values)的向量,输出是一个离散值,类(class)。
例如,一个用于垃圾邮件分类的过滤器,分类器将邮件分为垃圾邮件和非垃圾邮件,它的输入值可以是一个布尔向量x = (x1, . . . , xj, . . . , xd), xj = 1代表在字典的第j个单词出现在邮件中。学习过程是输入训练集样例xi,yi),其中 xi =(xi,1, . . . , xi,d)是输入
yi 是对应输出, 最终得到分类器(classifier)。 测试就是对测试得到的分类器是否能对没有见过的xt ,得到正确的yt。
(是否能准确判断新邮件是否是垃圾邮件)
2. Learning = Representation + Evaluation + Optimization
如果有一个情景你觉得很适合应用机器学习来解决,我们会面临的问题是我们到底先用哪种学习算法? 为了不会束手无措,我们应该抓住这三点,也是每种学习方法都具有的:
(1) Representation
一个分类器要可以被表示出来, 反过来讲为分类器选表达式, 要从一个集合中选,这个集合叫做假设空间(hypothesis space). 分类器的表达式不在假设空间, 我们就不会通过训练得到。 同时我们也会考虑一个相关的问题, 怎么表示我们的输入,也就是我们该用哪些feature?后面会阐述这个问题。
(2)Evaluation
评估函数(evaluation function, 也叫objective function or scoring function)用来区分好的分类器和坏的分类器。用在算法内部的评估函数和用在算法外部为了优化分类器的评估函数可能不一样。
(3) Optimization
选择合理的优化方法是提高学习效率的关键,常见的优化方法有Gradient descent algorithm和Stochastic gradient descent。
以下下表格是常见机器学习算法的以上三点:
Representation |
Evaluation |
Optimization |
Instances K-nearest neighbor Support vector machines Hyperplanes Naive Bayes Logistic regression Decision trees Sets of rules Propositional rules Logic programs Neural networks Graphical models Bayesian networks Conditional random fields |
Accuracy/Error rate Precision and recall Squared error Likelihood Posterior probability Information gain K-L divergence Cost/Utility Margin |
Combinatorial optimization Greedy search Beam search Branch-and-bound Continuous optimization Unconstrained Gradient descent Conjugate gradient Quasi-Newton methods Constrained Linear programming Quadratic programming |
3. 归纳(generalization)是关键
机器学习的重要目标就是从训练集中做归纳(generalize)。这是因为无论我们有多少数据, 我们碰到测试例和样本例相同的情况的几率是很小的,例如在字典中有 100000个单词,垃圾邮件的分类器就有2的100000次方的不同输入。对于刚学机器学习的人,常见的错误就是用训练集做测试,得到的结果好就认为成功了。其实这样再用新数据测试时,结果还不如随机的猜。所以我i们要留一些训练集之外的数据用来测试, 而不是所有数据用来训练得到我们的分类器。
有时我们会无意间用测试例污染我们的分类器,例如我们用测试集来大幅度调整参数。用一部分数据用来测试会导致训练集数据减少,我们用cross-validation来解决:随机把训练集分成十份,每一份都做测试集剩下的用来训练,最后取平均值。
4.仅仅有数据是不够的
把归纳作为目标,我们就要承认,仅仅有数据是不够的。例如从一百万的样本中学习一个100变量的布尔函数,仍然有个样本我们不知道他们的classes,在没有其他信息提供的情况下,最好的方法就是投掷硬币决定。这就是No FreeLunch theorems:无论学习算法a多聪明和学习算法b多笨拙,他们的期望性能相同。注意到,NFL定理有一个重要前提:所有“问题”出现的机会相同,或所有问题同等重要。NFL定理的简短论述过程中假设了我们要学习的函数是均匀分布但实际情况并不是这样。NFL定理最重要的寓意是:脱离具体问题,空谈什么学习算法更好毫无意义,因为若考虑所有潜在的问题,则所有的学习算法都一样好,要谈论算法的相对优劣,必须针对具体的学习问题,学习算法自身的归纳偏好与问题是否相配,往往会起到决定性作用。
5.过拟合(overfitting )的多角度
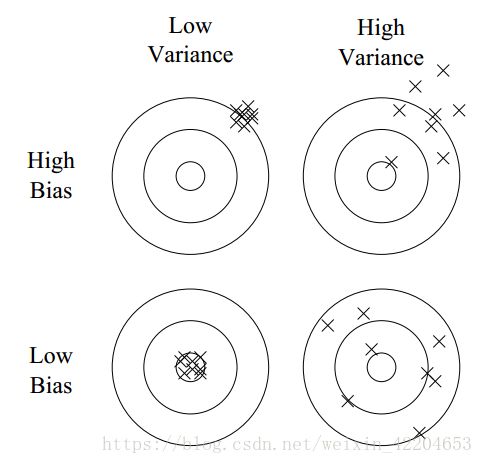
过拟合的概念不难,但是过拟合有很多并不明显的形式。 “偏差-方差分解”(bias and variance decomposing)是理解过拟合的一种方法。拿投掷飞镖的例子来说明:
线性learner具有高偏差,因为当两classes的边界不是超平面时(hyperplane),learner就不能推导。决策树就没有这个问题,因为决策树能表示任意布尔函数,但决策树有高方差:
(未完待续)