三叉树的题型
将有关二叉树的概念推广到三叉树,则一棵有244个结点的完全三叉树的高度为()
A.4
B.5
C.6
D.7
解析:
等比数列法:
等比数列求和 s=a1(1-q^n)/1-q
a1=1,q=3,∴s=(3^n-1)/2,得到n=6
注意按等比数列求和后得到的是满树的节点数,大于等于完全二叉树节点数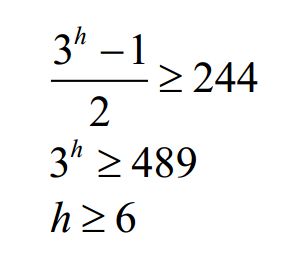
推导法:
考虑高度为1的,结点数为1 = 3^0
高度为2的,结点数最小为1+1=3^0+3^0 = 2,最大为1+3=3^0+3^1 = 4
.....3..............1 + 3 + 1 = 3^0+3^1+3^0 = 5,最大为1+3+9=3^0+3^1+3^2
高度为N的,结点数最小为1+3^1+3^2+...+3^(N-2)+3^0=(3^(N-1)+1)/2
最大为1+3^1+3^2+...+3^(N-2)+3^(N-1)=(3^N-1)/2
有n个结点时,则高度N满足
(3^(N-1)+1)/2<=n<=(3^N-1)/2
解之得到log3(2n+1)<=N<=log3(2n-1)+1
所以得到高度N为:
不小于log3(2n+1)的最小正整数或者不大于log3(2n-1)+1的最大正整数
再来一题
对N个结点深度为H的完全三叉树,N的最小值是多少?
解析:对于满三叉树每层结点个数:第一层3^0,第二层3^1,第三层3^2,.第h-1层3^(h-2).
第h层只有一个结点时是“对N个结点深度为H的完全三叉树,N值最小”
所以N=3^0+3^1+3^2+.+3^(h-2)+1=(3^(h-1)-1)/2+1
设某科三叉树中有40个结点,则该三叉树的最小高度为
解析:题意可以转化为一棵完全三叉树,此时根据上面提到的等比数列公式,马上能算出为4. 完美
来个难度高点的题
有一棵三叉树,度为1,2,3的节点数分别为n1,n2,n3,则该三叉数的叶子节点数n0为多少?
解析:设这棵树总节点数为n,边数为B,那么存在以下关系B=n-1,同时总节点数为n=n0+ n1+n2+n3,而树有这样的性质:有一个度为1的节点就有一条边,有一个度为2的节点就有两条边,依此类推,所以,B=n1+2*n2+3*n3(星号是乘,字母后面数字是下标),所以n0+n1+n2+n3=n1+2*n2+3*n3+1,所以n0=n2+2*n3+1,以此类推这个公式对度为m仍适用
总结:笔试时,博主我遇到的题是有深度求最多的节点数的,这时可以用等比数列求总数。
反想一下,完全三叉树深度为k的最多叶子节点数为多少呢?求第k-1层,再求k层,然后两者的总数相减。下次笔试再遇到三叉树的题就不虚了。
再来点二叉树的营养补补
(1) 在二叉树中,第i层的结点总数不超过2^(i-1);
(2) 深度为h的二叉树最多有2^h-1个结点(h>=1),最少有h个结点;
(3) 对于任意一棵二叉树,如果其叶结点数为N0,而度数为2的结点总数为N2,
则N0=N2+1;
(4) 具有n个结点的完全二叉树的深度为int(log2n)+1
(5)有N个结点的完全二叉树各结点如果用顺序方式存储,则结点之间有如下关系:
若I为结点编号则 如果I<>1,则其父结点的编号为I/2;
如果2*I<=N,则其左儿子(即左子树的根结点)的编号为2*I;若2*I>N,则无左儿子;
如果2*I+1<=N,则其右儿子的结点编号为2*I+1;若2*I+1>N,则无右儿子。
(6)给定N个节点,能构成h(N)种不同的二叉树。
h(N)为卡特兰数的第N项。h(n)=C(n,2*n)/(n+1)。