OpenGL与OpenCV实现增强现实

很久没有写博客了，最近在学习计算机视觉的相关知识，于是写了一个AR的小Demo。

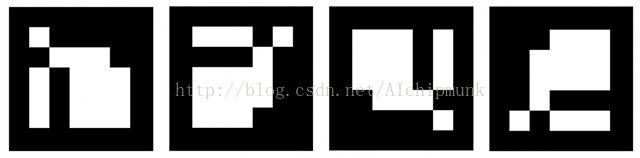
该程序通过OpenCV实现对Marker的识别和定位，然后通过OpenGL将虚拟物体叠加到摄像头图像下，实现增强现实。首先来看看我们使用的Marker：

这是众多Marker中的一个，它们都被一圈的黑色边框所包围，边框之中是编码信息，白色代表1，黑色代表0。将每一行作为一个字，那么每个字有5bits。其中，1、3、5位为校验位，2、4位为信息位。也就是说，整个Marker的信息位只有10bits，所以最多可表示1024个数（0~1023）。这种编码方式实际上是汉明码的变种，唯一区别在于它的首位是对应汉明码首位的反（比如汉明码是00000，那么Marker中的编码为10000）。这么做的目的是防止某一行全黑，从而提高识别率。汉明码还有另一大优势——不具有旋转对称性，因此程序能通过汉明码确定Marker的方向，因此从Marker中解码的信息是唯一的。

一、Marker的检测与识别

我们首先实现一个类，用于检测图像中的Marker，解码信息，并计算Marker相对于摄像头的坐标位置。

检测部分比较简单。首先将输入图像进行灰度变换，然后对灰度图像进行自适应二值化。之所以使用自适应二值化，是因为它能更好的适应光照的变化。但有一点要注意，很多朋友使用自适应二值化后表示得到的结果很像边缘检测的结果，那是因为自适应窗口过小造成的。使用自适应二值化时，窗口的大小应大于二值化目标的大小，否则得到的阈值不具有适应性。在自适应二值化之后，为了消除噪音或小块，可以加以形态学开运算。以上几部可分别得到下列图像（其中二值化的结果经过了反色处理，方便以后的轮廓提取）。

得到二值图像后，就可以使用OpenCV中的findContours来提取轮廓了。一副二值图像当中的轮廓有很多，其中有一些轮廓很小，我们通过一个阈值将这些过小的轮廓排除。排除过小轮廓后，就可以对轮廓进行多边形近似了。由于我们的Marker是正方形，其多边形近似结果应该满足以下条件：

1、只有4个顶点

2、一定是凸多边形

3、每一个边的长度不能过小

通过以上几个条件，我们可以排除绝大部分轮廓，从而找到最有可能为Marker的部分。找到这样的候选轮廓后，我们将它的多边形四个顶点保存下来，并做适当的调整，使所有顶点逆时针排序。代码如下：

 void MarkerRecognizer::markerDetect(Mat& img_gray, vector& possible_markers, int min_size, int min_side_length)
 {
     Mat img_bin;

     int thresh_size = (min_size/4)*2 + 1;
     adaptiveThreshold(img_gray, img_bin, 255, ADAPTIVE_THRESH_GAUSSIAN_C, THRESH_BINARY_INV, thresh_size, thresh_size/3);
     //threshold(img_gray, img_bin, 125, 255, THRESH_BINARY_INV|THRESH_OTSU);
     morphologyEx(img_bin, img_bin, MORPH_OPEN, Mat());  //use open operator to eliminate small patch

     vector> all_contours;
     vector> contours;
     findContours(img_bin, all_contours, CV_RETR_LIST, CV_CHAIN_APPROX_NONE);

     for (int i = 0; i < all_contours.size(); ++i)
     {
         if (all_contours[i].size() > min_size)
         {
             contours.push_back(all_contours[i]);
         }
     }

     vector approx_poly;
     for (int i = 0; i < contours.size(); ++i)
     {
         double eps = contours[i].size()*APPROX_POLY_EPS;
         approxPolyDP(contours[i], approx_poly, eps, true);

         if (approx_poly.size() != 4)
             continue;

         if (!isContourConvex(approx_poly))
             continue;

         //Ensure that the distance between consecutive points is large enough
         float min_side = FLT_MAX;
         for (int j = 0; j < 4; ++j)
         {
             Point side = approx_poly[j] - approx_poly[(j+1)%4];
             min_side = min(min_size, side.dot(side));
         }
         if (min_side < min_side_length*min_side_length)
             continue;

         //Sort the points in anti-clockwise
         Marker marker = Marker(0, approx_poly[0], approx_poly[1], approx_poly[2], approx_poly[3]);
         Point2f v1 = marker.m_corners[1] - marker.m_corners[0];
         Point2f v2 = marker.m_corners[2] - marker.m_corners[0];
         if (v1.cross(v2) > 0)    //由于图像坐标的Y轴向下，所以大于零才代表逆时针
         {
             swap(marker.m_corners[1], marker.m_corners[3]);
         }
         possible_markers.push_back(marker);
     }
 }

下一步，从这些候选区域中进一步筛选出真正的Marker。首先，由于摄像机视角的关系，图像中的Marker是经过透视变换的。为了方便提取Marker中的信息，要使用warpPerspective方法对候选区域进行透视变换，得到Marker的正视图。之后，由于Marker只有黑白两种颜色，其直方图分布是双峰的，所以用大津法（OTSU）对透视变换后的图像做二值化。

由于Marker都有一圈黑色的轮廓，这成为了我们进一步判定Marker的标准。获取正确的Marker图像后，可能有4个不同方向。这时我们就可以通过Marker中的汉明码确定Marker的正确朝向了，正确朝向的Marker，其汉明距离一定为零。得到Marker的朝向后，就可以提取Marker的信息（即ID），还可以调整Marker的4个顶点顺序，使其不随视角的变换而变换。在Demo中，我将正向放置的Marker的左上角作为1号顶点，逆时针旋转依次为2号、3号和4号。

代码如下：

 void MarkerRecognizer::markerRecognize(cv::Mat& img_gray, vector& possible_markers, vector& final_markers)
 {
     final_markers.clear();

     Mat marker_image;
     Mat bit_matrix(5, 5, CV_8UC1);
     for (int i = 0; i < possible_markers.size(); ++i)
     {
         Mat M = getPerspectiveTransform(possible_markers[i].m_corners, m_marker_coords);
         warpPerspective(img_gray, marker_image, M, Size(MARKER_SIZE, MARKER_SIZE));
         threshold(marker_image, marker_image, 125, 255, THRESH_BINARY|THRESH_OTSU); //OTSU determins threshold automatically.

         //A marker must has a whole black border.
         for (int y = 0; y < 7; ++y)
         {
             int inc = (y == 0 || y == 6) ? 1 : 6;
             int cell_y = y*MARKER_CELL_SIZE;

             for (int x = 0; x < 7; x += inc)
             {
                 int cell_x = x*MARKER_CELL_SIZE;
                 int none_zero_count = countNonZero(marker_image(Rect(cell_x, cell_y, MARKER_CELL_SIZE, MARKER_CELL_SIZE)));
                 if (none_zero_count > MARKER_CELL_SIZE*MARKER_CELL_SIZE/4)
                     goto __wrongMarker;
             }
         }

         //Decode the marker
         for (int y = 0; y < 5; ++y)
         {
             int cell_y = (y+1)*MARKER_CELL_SIZE;

             for (int x = 0; x < 5; ++x)
             {
                 int cell_x = (x+1)*MARKER_CELL_SIZE;
                 int none_zero_count = countNonZero(marker_image(Rect(cell_x, cell_y, MARKER_CELL_SIZE, MARKER_CELL_SIZE)));
                 if (none_zero_count > MARKER_CELL_SIZE*MARKER_CELL_SIZE/2)
                     bit_matrix.at(y, x) = 1;
                 else
                     bit_matrix.at(y, x) = 0;
             }
         }

         //Find the right marker orientation
         bool good_marker = false;
         int rotation_idx;   //逆时针旋转的次数
         for (rotation_idx = 0; rotation_idx < 4; ++rotation_idx)
         {
             if (hammingDistance(bit_matrix) == 0)
             {
                 good_marker = true;
                 break;
             }
             bit_matrix = bitMatrixRotate(bit_matrix);
         }
         if (!good_marker) goto __wrongMarker;

         //Store the final marker
         Marker& final_marker = possible_markers[i];
         final_marker.m_id = bitMatrixToId(bit_matrix);
         std::rotate(final_marker.m_corners.begin(), final_marker.m_corners.begin() + rotation_idx, final_marker.m_corners.end());
         final_markers.push_back(final_marker);

 __wrongMarker:
         continue;
     }
 }

得到最终的Marker后，为了之后计算精确的摄像机位置，还需对Marker四个顶点的坐标进行子像素提取，这一步很简单，直接使用cornerSubPix即可。

 void MarkerRecognizer::markerRefine(cv::Mat& img_gray, vector& final_markers)
 {
     for (int i = 0; i < final_markers.size(); ++i)
     {
         vector& corners = final_markers[i].m_corners;
         cornerSubPix(img_gray, corners, Size(5,5), Size(-1,-1), TermCriteria(CV_TERMCRIT_ITER, 30, 0.1));
     }
 }

为了检查算法的结果，将Marker的提取结果画到了图像上。其中蓝色边框标记了Marker的区域，空心圆圈代表Marker的1号顶点（正向放置时的左上角），较小的实心原点代表2号顶点，数字代表Marker的ID。

2、计算摄像机位置

计算摄像机的位置，首先需要对摄像机进行标定，标定是确定摄像机内参矩阵K的过程，一般用棋盘进行标定，这已经是一个很成熟的方法了，在这就不细说了。得到相机的内参矩阵K后，就可以使用solvePnP方法求取摄像机关于某个Marker的位置。摄像机成像使用小孔模型，如下：

x = K[R|T]X

其中，X是空间某点的坐标（相对于世界坐标系），[R|T]是摄像机外参矩阵，用于将某点的世界坐标变换为摄像机坐标，K是摄像机内参，用于将摄像机坐标中的某点投影的像平面上，x即为投影后的像素坐标。

对于一个确定的Marker，x是已知的，K是已知的，使用solvePnP求取相机位置实际上就是求取相机相对于Marker的外参矩阵[R|T]，但现在X还不知道，如何确定呢？

外参矩阵与世界坐标系的选取有关，而世界坐标系的选取是任意的，因此我们可以将世界坐标系直接设定在Marker上，如下图：

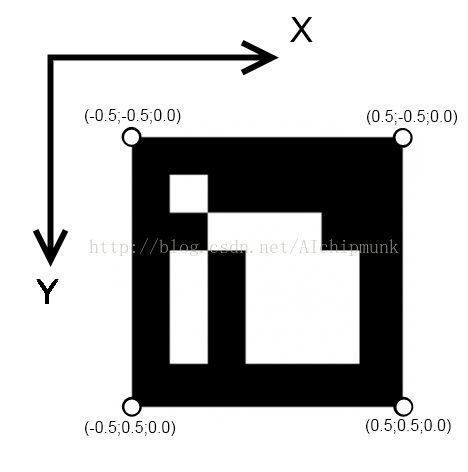
我们想象Marker位于世界坐标系的XY平面上（Z分量为零），且原点位于Marker的中心。由此，我们就确定了四个点的X坐标，将四个点的X坐标以及对应的像素坐标x传入solvePnP方法，即可得到相机关于该Marker的外参了。为了方便之后的使用，使用Rodrigues方法将旋转向量变为对应的旋转矩阵。

 void Marker::estimateTransformToCamera(vector corners_3d, cv::Mat& camera_matrix, cv::Mat& dist_coeff, cv::Mat& rmat, cv::Mat& tvec)
 {
     Mat rot_vec;
     bool res = solvePnP(corners_3d, m_corners, camera_matrix, dist_coeff, rot_vec, tvec);
     Rodrigues(rot_vec, rmat);
 }

那么现在问题来了！我们设定世界坐标系时，只设定了X轴与Y轴的方向，由于Z分量为零，它的方向并不影响求得的外参矩阵。但之后将虚拟物体放入该世界坐标时，却需要知道Z轴的方向，那么我们的Z轴方向到底是什么呢？

首先，solvePnP返回的结果是一个旋转向量和一个平移向量，两者构成一个刚体运动，刚体运动不会改变坐标系的手性（即右手坐标系经过刚体运动后还是右手坐标系），所以世界坐标系的手性应该和相机坐标系的手性一致。从相机的小孔成像模型中可以知道，相机坐标系的Z轴是指向像平面的，因此，通过下图我们可以断定，世界坐标系的Z轴是垂直于Marker向下的。

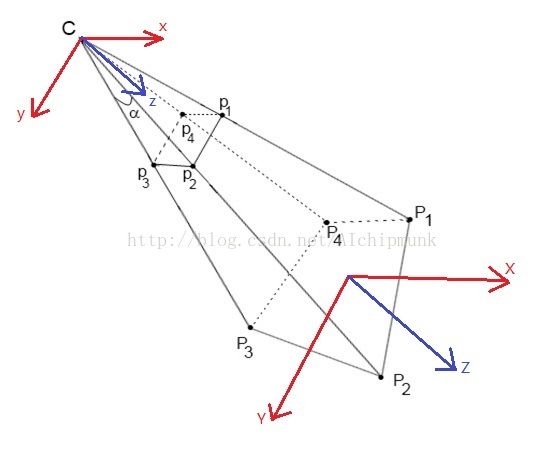
二、从OpenCV到OpenGL

得到摄像机的内参K和相对于每个Marker的外参[R|T]后，就可以开始考虑将虚拟物体添加进来了。老惯例，我还是使用OpenFrameworks。OpenFrameworks是在OpenGL基础上构建的一套框架，所以3D显示上，其本质还是OpenGL。

OpenGL的投影模型和普通相机的小孔投影模型是类似的，其PROJECTION矩阵对应与相机的内参K，MODELVIEW矩阵对应与相机的外参。但是，我们之前求得的K和[R|T]还不能直接使用，原因有二，其一，OpenGL投影模型使用的坐标系与OpenCV的不同；其二，OpenGL为了进行Clipping，其投影矩阵需要将点投影到NDC空间中。

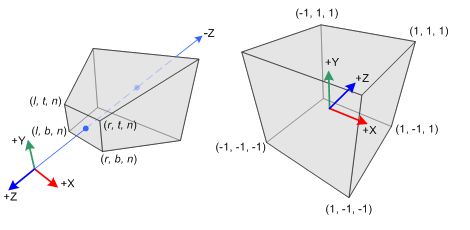
Perspective Frustum and Normalized Device Coordinates (NDC)

由上图（左边）可知，OpenGL的相机坐标系相当于OpenCV的相机坐标系绕着X轴旋转了180度，因此，我们使用外参矩阵[R|T]对世界坐标系中的某点进行变换后，还需要左乘一个旋转矩阵才能得到该点在OpenGL坐标系中的坐标。绕X轴旋转180度的旋转矩阵很简单，如下：

[ 1,  0,  0,

  0, -1,  0,

  0,  0, -1 ]

总之，外参矩阵[R|T]左乘以上矩阵后，即得OpenGL中的MODELVIEW矩阵，代码如下，注意OpenGL的矩阵元素是以列主序存储的。

 void ofApp::extrinsicMatrix2ModelViewMatrix(cv::Mat& rotation, cv::Mat& translation, float* model_view_matrix)
 {
     //绕X轴旋转180度，从OpenCV坐标系变换为OpenGL坐标系
     static double d[] =
     {
         1,  0,  0,
         0, -1,  0,
         0,  0, -1
     };
     Mat_<double> rx(3, 3, d);

     rotation = rx*rotation;
     translation = rx*translation;

     model_view_matrix[0] = rotation.at<double>(0,0);
     model_view_matrix[1] = rotation.at<double>(1,0);
     model_view_matrix[2] = rotation.at<double>(2,0);
     model_view_matrix[3] = 0.0f;

     model_view_matrix[4] = rotation.at<double>(0,1);
     model_view_matrix[5] = rotation.at<double>(1,1);
     model_view_matrix[6] = rotation.at<double>(2,1);
     model_view_matrix[7] = 0.0f;

     model_view_matrix[8] = rotation.at<double>(0,2);
     model_view_matrix[9] = rotation.at<double>(1,2);
     model_view_matrix[10] = rotation.at<double>(2,2);
     model_view_matrix[11] = 0.0f;

     model_view_matrix[12] = translation.at<double>(0, 0);
     model_view_matrix[13] = translation.at<double>(1, 0);
     model_view_matrix[14] = translation.at<double>(2, 0);
     model_view_matrix[15] = 1.0f;
 }

下一步是求PROJECTION矩阵。由于OpenGL要做Clipping，要求所有在透视椎体中的点都投影到NDC中，在NDC中的点能够显示在屏幕上，之外的点则不能。因此，我们的PROJECTION矩阵不仅要有与内参矩阵K相同的透视效果，还得把点投影到NDC中。

首先先看看内参矩阵K的形式：

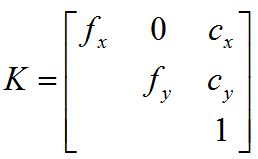
首先假设OpenGL的投影椎体是对称的，那么PROJECTION矩阵的形式如下：

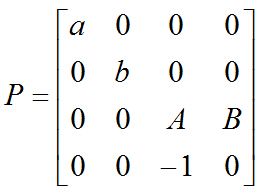
使用以上矩阵对某一点（X, Y, Z, 1）投影后，可以得到如下关系：

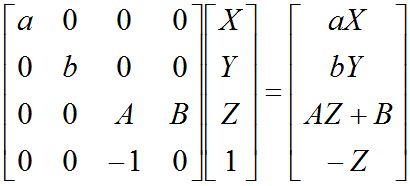
接下来，OpenGL会对该结果进行Clipping，具体方法是将四个分量都除以-Z，那么，要使我们的点最终显示到屏幕上，前三个分量在除以-Z后其变化范围必须在[-1, 1]内。如下：

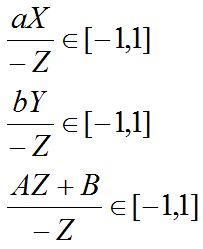
由摄像机投影模型（相似三角形）知：

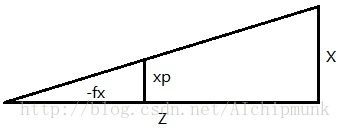
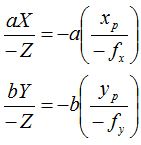
其中由于OpenGL相机的相面在Z轴负方向上，所以是-fx和-fy。xp和yp分别为某点在相面上的横坐标和纵坐标，这两个坐标的原点在图像的中心，图像的宽度和高度分别为w和h，因此xp和yp的取值范围分别为[-w/2, w/2]和[-h/2, h/2]，可得：

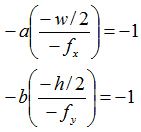
于是

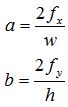
接下来，我们为OpenGL相机设定两个面，near和far，只有处于这两个面之间的点才能投影到NDC空间中，所以当 Z=-n 时，(AZ+B)/-Z = -1，当 Z=-f 时，(AZ+B)/-Z = 1，由此我们可以得到关于A和B的二元一次方程，从而解出A、B：

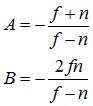
现在再来考虑OpenGL投影椎体不对称的情况，这种情况下，PROJECTION矩阵的形式为：

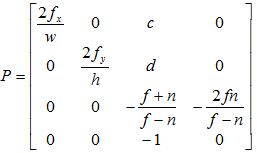
由于椎体不对称，这时xp和yp的变化范围分别为[l, r]和[b, t]，代表图像左侧（left）右侧（right），以及底部（bottom）顶部（top），用同样的方法，我们有：

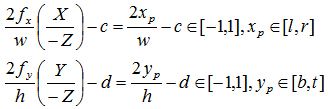
可得：

  ，  

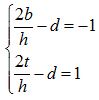
于是：

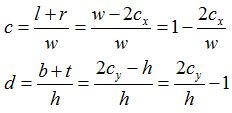
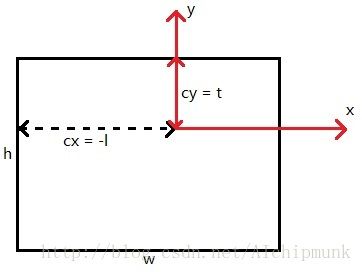
关于l+r和b+t是怎么计算的，可以参考下图：

综上所述，我们可以得到OpenGL投影矩阵的最终形式：

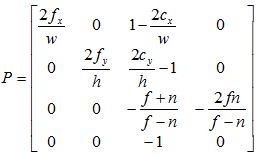
到此，我们就可以将这个矩阵的数据传递给PROJECTION矩阵了：

 void ofApp::intrinsicMatrix2ProjectionMatrix(cv::Mat& camera_matrix, float width, float height, float near_plane, float far_plane, float* projection_matrix)
 {
     float f_x = camera_matrix.at<float>(0,0);
     float f_y = camera_matrix.at<float>(1,1);

     float c_x = camera_matrix.at<float>(0,2);
     float c_y = camera_matrix.at<float>(1,2);

     projection_matrix[0] = 2*f_x/width;
     projection_matrix[1] = 0.0f;
     projection_matrix[2] = 0.0f;
     projection_matrix[3] = 0.0f;

     projection_matrix[4] = 0.0f;
     projection_matrix[5] = 2*f_y/height;
     projection_matrix[6] = 0.0f;
     projection_matrix[7] = 0.0f;

     projection_matrix[8] = 1.0f - 2*c_x/width;
     projection_matrix[9] = 2*c_y/height - 1.0f;
     projection_matrix[10] = -(far_plane + near_plane)/(far_plane - near_plane);
     projection_matrix[11] = -1.0f;

     projection_matrix[12] = 0.0f;
     projection_matrix[13] = 0.0f;
     projection_matrix[14] = -2.0f*far_plane*near_plane/(far_plane - near_plane);
     projection_matrix[15] = 0.0f;
 }

现在是时候放一些虚拟物体进来了，为了简单，我就放了几个立方体，由于OpenFrameworks绘制立方体时以立方体在中心为原点，所以为了使立方体的底面贴在Marker上，必须在Marker上方二分之一立方体边长的地方绘制，也就是绘制立方体的坐标为（0, 0, -0.5*size），为什么是负0.5呢？还记得之前所说的世界坐标系的Z轴是垂直于Marker并朝下的吗？所以要画在Marker上方，必须向Z轴负方向移动！

 void ofApp::draw(){

     ofSetColor(255);
     float view_width = ofGetViewportWidth();
     float view_height = ofGetViewportHeight();
     m_video.draw(0, 0, view_width, view_height);

     //Set camera matrix to the opengl projection matrix;
     intrinsicMatrix2ProjectionMatrix(m_camera_matrix, 640, 480, 0.01f, 100.0f, m_projection_matrix);
     ofSetMatrixMode(OF_MATRIX_PROJECTION);
     //Openframeworks里将(-1, -1)映射到屏幕左上角，而非一般的左下角，所以需要一个矩阵进行垂直镜像
     static float reflect[] =
     {
         1,  0, 0, 0,
         0, -1, 0, 0,
         0,  0, 1, 0,
         0,  0, 0, 1
     };
     ofLoadMatrix(reflect);
     //OpenGL默认为右乘
     ofMultMatrix(m_projection_matrix);

     //Reset model view matrix to identity;
     ofSetMatrixMode(OF_MATRIX_MODELVIEW);
     ofLoadIdentityMatrix();

     //Set opengl parameters
     ofSetColor(255);
         ofEnableBlendMode(OF_BLENDMODE_ALPHA);
     ofEnableDepthTest();
         glShadeModel(GL_SMOOTH); //some model / light stuff
         m_light.enable();
         ofEnableSeparateSpecularLight();

     vector& markers = m_recognizer.getMarkers();
     Mat r, t;
     for (int i = 0; i < markers.size(); ++i)
     {
         //求出的旋转矩阵r的行列式为+1，即为刚体变换，所以不改变坐标系的手性
         markers[i].estimateTransformToCamera(m_corners_3d, m_camera_matrix, m_dist_coeff, r, t);
         extrinsicMatrix2ModelViewMatrix(r, t, m_model_view_matrix);
         ofLoadMatrix(m_model_view_matrix);

         ofSetColor(0x66,0xcc,0xff);
         //由于Marker坐标系与OpenCV坐标系的手性一致，所以Marker坐标系的Z轴垂直于Marker向下
         //绘制Box时的Anchor在Box中心，所以需要-0.5*size的偏移才能使Box的底面在Marker上！！
         ofDrawBox(0, 0, -0.4f, 0.8f);
     }

     //Reset parameters
     ofDisableDepthTest();
         m_light.disable();
         ofDisableLighting();
         ofDisableSeparateSpecularLight();

     ofSetMatrixMode(OF_MATRIX_MODELVIEW);
     ofLoadIdentityMatrix();
     ofSetMatrixMode(OF_MATRIX_PROJECTION);
     ofLoadIdentityMatrix();
 }

注意，我在设置投影矩阵时，左乘了一个垂直方向的镜像矩阵，这是因为，我发现OpenFrameworks将NDC空间中（-1, -1）点映射到屏幕的左上角，而非一般OpenGL所映射的左下角，如果不乘这个镜像矩阵，得到的图像就是上下颠倒的。至于为什么OpenFrameworks是这样，由于没仔细研究它的代码，我只能猜测是其在初始化时对OpenGL做了一些设置所致。所以，如果我的理解或猜测有错误，还请大家指出^_^

最后给出代码的下载地址，程序用VS2012开发，解压后放到”OpenFrameworks安装目录\apps\myApps“下打开编译：

http://download.csdn.net/detail/aichipmunk/8207875