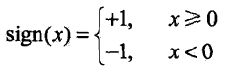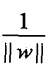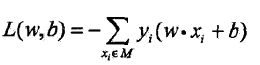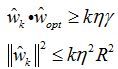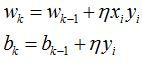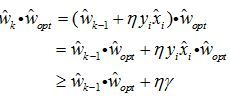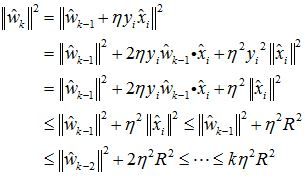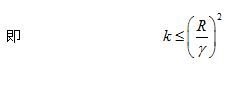【统计学习方法-李航-笔记总结】二、感知机（感知机的原始形式与对偶形式）

本文是李航老师《统计学习方法》第二章的笔记，欢迎大佬巨佬们交流。

主要包括以下几部分：

1. 感知机模型

2. 感知机策略

3. 感知机算法

 

1. 感知机模型

    感知机是二分类的线性分类模型，其输入为实例的特征向量，输出为实例的类别，取+1和-1两个值。感知机旨在求出将训练数据进行线性划分的超平面，为此利用基于误分类的损失函数，利用梯度下降对其极小化，求得感知机模型。

定义：假设输入空间（特征空间）是X∈,输出空间是Y={-1,+1}，输入x∈X表示实例的特征向量，对应于输入空间（特征空间）的点，输出y∈Y表示的实例类别，由输入空间到输出空间的如下函数成为感知机。

                                                      

其中：w为权值，b为偏置，wx表示w和x的内积，sign是符号函数，即：

                                                       

感知机模型的假设空间是定义在特征空间中的所有线性分类模型，即函数集合

感知机有如下解释：线性方程对应于特征空间中的一个超平面S，其中w是超平面的法向量，b是超平面的截距，这个超平面将特征空间划分为两个部分，位于两部分的点（特征向量）分别为正类和负类

                                                

感知机模型主要求w和b，从而对新的实例给出预测。

2. 学习策略

（1）线性可分数据集：给定一个数据集，其中，，如果存在某个超平面S，，能够将数据集的正实例点和负实例点完全正确地划分到超平面两侧，则称数据集T为线性可分数据集。

（2）损失函数：损失函数的一个自然的选择是误分类点总数，但是这样的损失函数不是参数w,b的连续可导函数，不易优化，因此考虑另一种选择，即计算误分类点到超平面S的总距离。

首先，已知点（x0,y0）到直线Ax+By+C=0的距离公式为：

那么输入空间中的任一点x0到超平面的距离为：，||w||是w的L2范数

其次，对于误分类的数据来说，有：，因为当时，yi = -1，而时，yi=+1

因此，误分类点xi到超平面S的距离为：

这样，假设超平面S的误分类点集合为M，那么所有误分类点到超平面S的总距离是：

不考虑，则感知机的损失函数为：

若没有误分类的点，损失函数值为0，误分类点越少，函数值越小，该函数是w,b的连续可导函数。

3. 感知机学习算法

（1）算法的原始形式（相对于对偶形式）：

优化感知机就是求其损失函数极小化的过程：

优化的过程是采用随机梯度下降法，任意选取一个超平面w0,b0（初始值，初始值不同时结果也不同）,每次随机选取一个误分类点使其梯度下降，直至所有的误分类点都被选取过。

假设误分类点集合M是固定的，那么损失函数L(w,b)的梯度为：

                                                                

随机选取一个误分类点（xi,yi），对w,b进行更新，直到yi(wxi+b)>0停止更新：

                                                                   

η是学习率，0≤η≤1

这里区分两个概念：

梯度下降：一次将误分类集合中所有误分类点的梯度下降；

 随机梯度下降：随机选取一个误分类点使其梯度下降。

算法流程描述如下：

上述过程的直观解释是：当一个实例点被误分类，也就是说它位于分类超平面的错误一侧时，调整w,b的值，使分类超平面向该误分类点的一侧移动，以减少该误分类点与超平面的距离，直至超平面越过该误分类点，使其被正确分类。

（2）算法的收敛性：

通俗的理解，模型优化算法收敛就是经过有限次迭代后，模型的损失函数趋近于0（或者接近0的值），也就是说，对于线性可分数据集，感知机模型算法收敛即是经过有限次迭代后，可以得到一个将训练数据集完全正确划分的分离超平面。

此处有Novikoff定理：

证明（1）由于数据集线性可分，据线性可分的定义，存在超平面可将训练集数据完全正确分开，取此超平面为：，由于有限的i = 1,2,...,N,均有，

所以存在，使

证明（2）

首先证明两个不等式：

                                                                    

证明第一个：

令感知机算法的初始值为

若存在实例误分类，则需要不断更新权重，令wk-1是进行第k个误分类之前的权重，即

                                                                      

                                                            

则第k步更新过程为

                                                                       

则

则

递推上述不等式，得

证明第二个不等式：

                                              

综合上述：

                                      

                                    

上述定理表明，误分类次数k是有上界的，即经过有限次搜索，可以找到将训练集数据完全正确分开的分类超平面，也就是说，当训练集数据线性可分时，感知学习算法的原始形式迭代是收敛的。我们对(2)中的R与γ进行理解。如果R越大，也就是max||x^i||越大，此时相当于有一个点距离原点很远，在初始化时，我们常常初始化w=0，b=0，所以我们要到达正确的分界面所需要的迭代次数也就越多，因此上界越大；如果γ越小，即min{yi(wopt⋅xi+bopt)}越小，也就是说，对于点xi，yi来说，虽然它被正确分类，但是它离最优分界面wopt，bopt很近，所以很容易就因为在对其它点进行更新时，导致这个点被误分类，因而迭代次数的上界越大。 

引申：由上述可知，感知机算法存在许多解，这些解即依赖于初值的选择，又依赖于迭代中误分类点的选择顺序，为了得到唯一的超平面，要对分类超平面增加约束条件，这就是后面支持向量机的想法。当训练集线性不可分时，感知机学习孙发不收敛，迭代结果将发生震荡。

（3）感知机的对偶形式

对偶形式的基本想法是，将w和b表示为实例xi和标记yi的线性组合的形式，通过求解其系数而求得w和b。

对于初值w0和b0,误分类点(xi,yi),通过逐步修改w,b，设修改n次，则w和b关于(xi,yi)的增量分别是，这里，则最后学到的w和b可以表示为：

算法流程描述如下：

   

α相当于把原始形式中的w写成展开形式，所以更新时只加η就够了，b还用的原始形式，没有变。

感知学习算法的对偶形式的迭代是收敛的，与原始形式一样，存在多个解。

对偶形式中的训练实例以内积出现，为了方便，可以先计算实例间两两的内积，存储为矩阵，即Gram矩阵，

 

感知机中的原始形式与对偶形式与支持向量机是对应的，接下来将更新支持向量机的部分。

参考文献：

《统计学习方法》，李航