拉格朗日乘数法(Lagrange multiplier)
先摆公式,再说推导。
求二元函数 z = f ( x , y ) z=f(x,y) z=f(x,y)在条件 φ ( x , y ) = 0 \varphi(x,y)=0 φ(x,y)=0下的极值。
(1)作Lagrange函数
F ( x , y , λ ) = f ( x , y ) + λ φ ( x , y ) ; F(x,y,\lambda)=f(x,y)+\lambda\varphi(x,y); F(x,y,λ)=f(x,y)+λφ(x,y);
(2)求 F ( x , y , λ ) F(x,y,\lambda) F(x,y,λ)的驻点 ( x 0 , y 0 , λ 0 ) (x_0,y_0,\lambda_0) (x0,y0,λ0)
F x = f x ( x , y ) + λ ⋅ φ x ( x , y ) = 0 ; F y = f y ( x , y ) + λ ⋅ φ y ( x , y ) = 0 ; F λ = φ ( x , y ) = 0 \begin{aligned} F_x&=f_x(x,y)+\lambda\cdot\varphi_x(x,y)=0; \\ F_y&=f_y(x,y)+\lambda\cdot\varphi_y(x,y)=0; \\ F_{\lambda}&=\varphi(x,y)=0 \end{aligned} FxFyFλ=fx(x,y)+λ⋅φx(x,y)=0;=fy(x,y)+λ⋅φy(x,y)=0;=φ(x,y)=0
(3) ( x 0 , y 0 ) (x_0,y_0) (x0,y0)便是可能的条件极值点
拉格朗日乘数法所得的极点会包含原问题的所有极值点,但并不保证每个极值点都是原问题的极值点。(维基百科)
例如,目标函数: z = x y z=xy z=xy,约束条件: x + y = 1 x+y=1 x+y=1
解: 作Lagrange函数
F ( x , y , λ ) = x y + λ ( x + y − 1 ) F(x,y,\lambda)=xy+\lambda(x+y-1) F(x,y,λ)=xy+λ(x+y−1)
求F的驻点:
F x = y + λ = 0 F y = x + λ = 0 F λ = x + y − 1 = 0 ⟹ x = 1 2 ; y = 1 2 ; λ = − 1 2 \begin{aligned} F_x&=y+\lambda=0\\ F_y&=x+\lambda=0\\ F_{\lambda}&=x+y-1=0\\ \implies &x=\frac{1}{2};y=\frac{1}{2};\lambda=-\frac{1}{2} \end{aligned} FxFyFλ⟹=y+λ=0=x+λ=0=x+y−1=0x=21;y=21;λ=−21
公式推导
条件极值: 在一定约束条件下(一般为方程)的极值就称为条件极值。
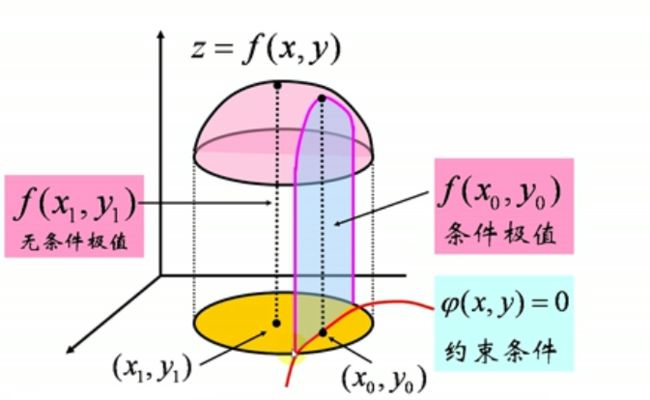
条件极值的几何解释:
约束条件 φ ( x , y ) = 0 \varphi(x,y)=0 φ(x,y)=0是指,在曲线 φ ( x , y ) \varphi(x,y) φ(x,y)上取一点,使得 f ( x , y ) f(x,y) f(x,y)有极值(由图可知为极大值)
条件极值的必要条件:
函数 z = f ( x , y ) z=f(x,y) z=f(x,y)在条件 φ ( x , y ) = 0 \varphi(x,y)=0 φ(x,y)=0,下的极值的必要条件是什么?
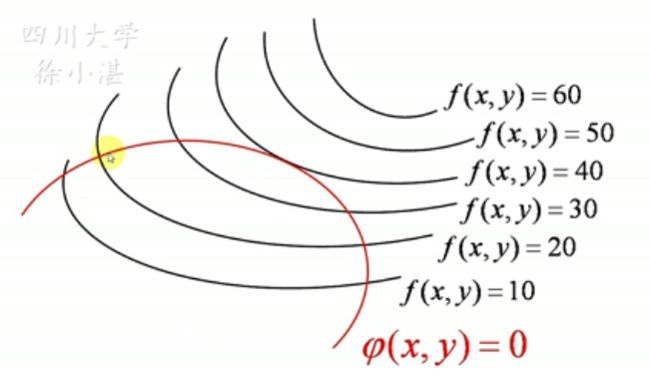
先看一个比较直观的图
图中黑色曲线为 z = f ( x , y ) z=f(x,y) z=f(x,y)的等值线,红色曲线为约束条件 φ ( x , y ) = 0 \varphi(x,y)=0 φ(x,y)=0,那么函数 f ( x , y ) f(x,y) f(x,y)在哪里取得条件最大值?
推导:
设 z 0 = f ( x 0 , y 0 ) z_0=f(x_0,y_0) z0=f(x0,y0)是 z = f ( x , y ) z=f(x,y) z=f(x,y)在条件 φ ( x , y ) = 0 \varphi(x,y)=0 φ(x,y)=0下的条件极值。设 y = y ( x ) y=y(x) y=y(x)是约束条件 φ ( x , y ) = 0 \varphi(x,y)=0 φ(x,y)=0所确定的隐函数。
则: z = f ( x , y ( x ) ) z=f(x,y(x)) z=f(x,y(x))此时就变成了一个一元函数,且在 x = x 0 x=x_0 x=x0处取得极值。
(1)由一元函数极值的必要条件可知:(若 f ( x ) f(x) f(x)在 x = x 0 x=x_0 x=x0处取得极值,且 f ′ ( x 0 ) f'(x_0) f′(x0)存在,则有 f ′ ( x 0 ) = 0 f'(x_0)=0 f′(x0)=0)
所以有:
d z d x = f x ⋅ 1 + f y ⋅ d y d x = 0 ⟹ f x ( x 0 , y 0 ) + f y ( x 0 , y 0 ) ⋅ y ′ ( x 0 ) = 0 ⟹ y ′ ( x 0 ) = − f x ( x 0 , y 0 ) f y ( x 0 , y 0 ) (1) \begin{aligned} \frac{dz}{dx}&=f_x\cdot1+f_y\cdot\frac{dy}{dx}=0 \\ \implies&f_x(x_0,y_0)+f_y(x_0,y_0)\cdot y'(x_0)=0 \\ \implies&y'(x_0)=-\frac{f_x(x_0,y_0)}{f_y(x_0,y_0)} \tag 1 \end{aligned} dxdz⟹⟹=fx⋅1+fy⋅dxdy=0fx(x0,y0)+fy(x0,y0)⋅y′(x0)=0y′(x0)=−fy(x0,y0)fx(x0,y0)(1)
(2)由隐函数求导公式可知
y ′ ( x 0 ) = − φ x ( x 0 , y 0 ) φ y ( x 0 , y 0 ) 由 ( 1 ) ( 2 ) ⟹ f x ( x 0 , y 0 ) f y ( x 0 , y 0 ) = φ x ( x 0 , y 0 ) φ y ( x 0 , y 0 ) ⟹ f x ( x 0 , y 0 ) φ x ( x 0 , y 0 ) = f y ( x 0 , y 0 ) φ y ( x 0 , y 0 ) (2) \begin{aligned} y'(x_0)&=-\frac{\varphi_x(x_0,y_0)}{\varphi_y(x_0,y_0)}\tag 2\\ \\ 由(1)(2) \implies&\frac{f_x(x_0,y_0)}{f_y(x_0,y_0)}=\frac{\varphi_x(x_0,y_0)}{\varphi_y(x_0,y_0)}\\\\ \implies&\frac{f_x(x_0,y_0)}{\varphi_x( x_0,y_0)}=\frac{f_y(x_0,y_0) }{\varphi_y(x_0,y_0)} \end{aligned} y′(x0)由(1)(2)⟹⟹=−φy(x0,y0)φx(x0,y0)fy(x0,y0)fx(x0,y0)=φy(x0,y0)φx(x0,y0)φx(x0,y0)fx(x0,y0)=φy(x0,y0)fy(x0,y0)(2)
那么此时我们可以理解成 { f x ( x 0 , y 0 ) , f y ( x 0 , y 0 ) } / / { φ x ( x 0 , y 0 ) , φ y ( x 0 , y 0 ) } \{f_x(x_0,y_0),f_y(x_0,y_0)\}//\{\varphi_x( x_0,y_0),\varphi_y( x_0,y_0)\} {fx(x0,y0),fy(x0,y0)}//{φx(x0,y0),φy(x0,y0)},即两个向量平行
⟹ Δ f ( x 0 , y 0 ) / / Δ φ ( x 0 , y 0 ) \implies\Delta f(x_0,y_0)//\Delta \varphi(x_0,y_0) ⟹Δf(x0,y0)//Δφ(x0,y0)
我们知道某一点的梯度就是,该点所在平面对应的一个法向量。(知道的可以略过这点,不知道的接着往下看)
证明:
设二元函数 F ( x , y ) = 0 F(x,y)=0 F(x,y)=0,则其在点 x = x 0 x=x_0 x=x0处的斜率 k = − F x ( x 0 , y 0 ) F y ( x 0 , y 0 ) k=-\frac{F_x(x_0,y_0)}{F_y(x_0,y_0)} k=−Fy(x0,y0)Fx(x0,y0).设 A ( x 1 , y 1 ) , B ( x 2 , y 2 ) A(x_1,y_1),B(x_2,y_2) A(x1,y1),B(x2,y2)为该切线上的两个点,则k又可以写成 k = y 2 − y 1 x 2 − x 1 k=\frac{y_2-y_1}{x_2-x_1} k=x2−x1y2−y1
⟹ A B → = ( x 2 − x 1 , y 2 − y 1 ) ⟹ 1 x 2 − x 1 ⋅ A B → = ( 1 , y 2 − y 1 x 2 − x 1 ) ⟹ λ ⋅ A B → = ( 1 , k ) = ( 1 , − F x ( x 0 , y 0 ) F y ( x 0 , y 0 ) ) ⟹ λ ⋅ F y ( x 0 , y 0 ) ⋅ A B → = ( F y ( x 0 , y 0 ) , − F x ( x 0 , y 0 ) ) ⟹ μ ⋅ A B → = ( F y ( x 0 , y 0 ) , − F x ( x 0 , y 0 ) ) \begin{aligned} \implies& \overrightarrow{AB}=(x_2-x_1,y_2-y_1)\\\\ \implies&\frac{1}{x_2-x_1}\cdot\overrightarrow{AB}=(1,\frac{y_2-y_1}{x_2-x_1})\\ \\ \implies&\lambda\cdot\overrightarrow{AB}=(1,k)=(1,-\frac{F_x(x_0,y_0)}{F_y(x_0,y_0)})\\ \\ \implies&\lambda\cdot F_y(x_0,y_0)\cdot\overrightarrow{AB}=(F_y(x_0,y_0),-F_x(x_0,y_0))\\ \\ \implies&\mu\cdot\overrightarrow{AB}=(F_y(x_0,y_0),-F_x(x_0,y_0)) \end{aligned} ⟹⟹⟹⟹⟹AB=(x2−x1,y2−y1)x2−x11⋅AB=(1,x2−x1y2−y1)λ⋅AB=(1,k)=(1,−Fy(x0,y0)Fx(x0,y0))λ⋅Fy(x0,y0)⋅AB=(Fy(x0,y0),−Fx(x0,y0))μ⋅AB=(Fy(x0,y0),−Fx(x0,y0))
于是我们可以得到的结论就是,若直线斜率为k,则他的一个方向向量为 a ⃗ = ( 1 , k ) \vec{a}=(1,k) a=(1,k)
我们又知道, F ( x , y ) = 0 F(x,y)=0 F(x,y)=0在点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)处,所在平面(曲面在某一点的切平面)的法向量,垂直于该点所在平面的任意直线,当然也就包括切于该点的所有切线。于是该点法线的斜率 k ′ = − 1 k k'=-\frac{1}{k} k′=−k1。
法 线 的 一 个 方 向 向 量 为 a ⃗ = ( 1 , − 1 k ) = ( 1 , F y ( x 0 , y 0 ) F x ( x 0 , y 0 ) ) a ⃗ ⋅ F x ( x 0 , y 0 ) = ( F x ( x 0 , y 0 ) , F y ( x 0 , y 0 ) ) \begin{aligned} 法线的一个方向向量为\vec{a}&=(1,-\frac{1}{k})=(1,\frac{F_y(x_0,y_0)}{F_x(x_0,y_0)})\\\\ \vec{a}\cdot F_x(x_0,y_0)&=(F_x(x_0,y_0),F_y(x_0,y_0))\\ \\ \end{aligned} 法线的一个方向向量为aa⋅Fx(x0,y0)=(1,−k1)=(1,Fx(x0,y0)Fy(x0,y0))=(Fx(x0,y0),Fy(x0,y0))
所以取 a ⃗ = ( F x ( x 0 , y 0 ) , F y ( x 0 , y 0 ) ) = Δ F ( x 0 , y 0 ) \vec{a}=(F_x(x_0,y_0),F_y(x_0,y_0))=\Delta F(x_0,y_0) a=(Fx(x0,y0),Fy(x0,y0))=ΔF(x0,y0), F x ( x 0 , y 0 ) F_x(x_0,y_0) Fx(x0,y0)为常数,不影响。
证毕
由 Δ f ( x 0 , y 0 ) / / Δ φ ( x 0 , y 0 ) \Delta f(x_0,y_0)//\Delta \varphi(x_0,y_0) Δf(x0,y0)//Δφ(x0,y0)可知:
∃ λ 0 , 使 得 Δ f ( x 0 , y 0 ) = − λ 0 ⋅ Δ φ ( x 0 , y 0 ) ⟹ Δ f ( x 0 , y 0 ) + λ 0 ⋅ Δ φ ( x 0 , y 0 ) = 0 ⃗ ⟹ Δ { f ( x 0 , y 0 ) + λ 0 ⋅ φ ( x 0 , y 0 ) } = 0 ⃗ ⟹ Δ ( f + λ 0 φ ) = 0 ⃗ \begin{aligned} \exists \lambda_0,使得&\Delta f(x_0,y_0)=-\lambda_0\cdot\Delta \varphi(x_0,y_0) \\ \\ \implies&\Delta f(x_0,y_0)+\lambda_0\cdot\Delta \varphi(x_0,y_0) =\vec{0}\\ \\ \implies&\Delta \{f(x_0,y_0)+\lambda_0\cdot\varphi(x_0,y_0)\} =\vec{0}\\ \\ \implies&\Delta(f+\lambda_0\varphi)=\vec{0} \end{aligned} ∃λ0,使得⟹⟹⟹Δf(x0,y0)=−λ0⋅Δφ(x0,y0)Δf(x0,y0)+λ0⋅Δφ(x0,y0)=0Δ{f(x0,y0)+λ0⋅φ(x0,y0)}=0Δ(f+λ0φ)=0
此时我们可以用最原始的定义来求解上面的例题,即:
Δ z ( x , y ) + λ ⋅ Δ φ ( x , y ) = 0 ⃗ ⟹ ( y , x ) + λ ( 1 , 1 ) = 0 ⃗ (分别求梯度) ⟹ y + λ = 0 , x + λ = 0 ⟹ x = y = − λ x + y = 1 , ⟹ x = y = 1 2 , λ = − 1 2 \begin{aligned} &\Delta z(x,y)+\lambda\cdot\Delta \varphi(x,y) =\vec{0}\\ \implies&(y,x)+\lambda(1,1)=\vec{0}\text{(分别求梯度)}\\ \implies&y+\lambda=0,x+\lambda=0\\ \implies&x=y=-\lambda\\ x+y=1,\implies&x=y=\frac{1}{2},\lambda=-\frac{1}{2} \end{aligned} ⟹⟹⟹x+y=1,⟹Δz(x,y)+λ⋅Δφ(x,y)=0(y,x)+λ(1,1)=0(分别求梯度)y+λ=0,x+λ=0x=y=−λx=y=21,λ=−21
由此我们可以得到的结论是:
令函数 F ( x , y , λ ) = f ( x , y ) + λ φ ( x , y ) F(x,y,\lambda)=f(x,y)+\lambda\varphi(x,y) F(x,y,λ)=f(x,y)+λφ(x,y),若 Δ F ( x 0 , y 0 , λ 0 ) = 0 ⃗ \Delta F(x_0,y_0,\lambda_0)=\vec{0} ΔF(x0,y0,λ0)=0,则 ( x 0 , y 0 , λ 0 ) (x_0,y_0,\lambda_0) (x0,y0,λ0)是函数 F ( x , y , λ ) F(x,y,\lambda) F(x,y,λ)的驻点,通过如下步骤,就可以就得驻点的值。
{ F x = 0 F y = 0 F λ = 0 \begin{aligned} \begin{cases}F_x=0\\ F_y=0\\ F_\lambda=0 \end{cases} \end{aligned} ⎩⎪⎨⎪⎧Fx=0Fy=0Fλ=0
F ( x , y , λ ) F(x,y,\lambda) F(x,y,λ)称为拉格朗日函数, λ \lambda λ称为拉格朗日乘数(Lagrange multiplier)
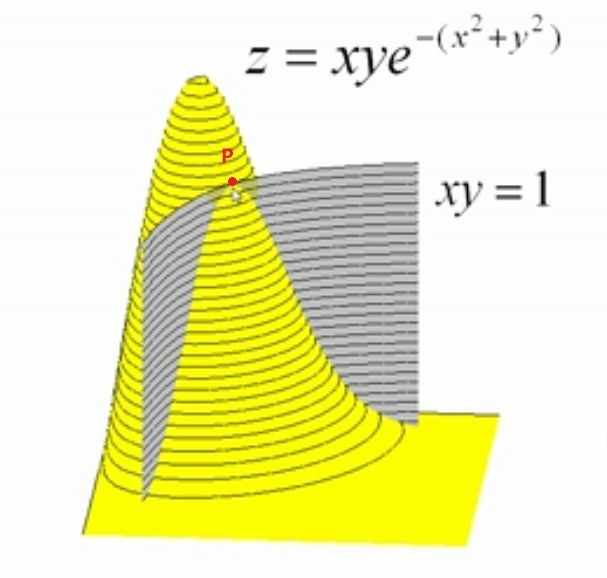
另外,由下图也可以直观的看出,在约束条件下, z = x y e − ( x 2 + y 2 ) z=xye^{-(x^2+y^2)} z=xye−(x2+y2)取得极值。且此时, z = x y e − ( x 2 + y 2 ) z=xye^{-(x^2+y^2)} z=xye−(x2+y2)在点P处的法向量与 x y = 1 xy=1 xy=1在P处的法向量平行。
更正:等值线 x y e − ( x 2 + y 2 ) = z 0 xye^{-(x^2+y^2)}=z_0 xye−(x2+y2)=z0在 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)(条件极值)处的法向量平行于 x y − 1 = 0 xy-1=0 xy−1=0在 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)处的法向量。
易知 z = x y e − ( x 2 + y 2 ) z=xye^{-(x^2+y^2)} z=xye−(x2+y2) 在 ( 1 , 1 , e − 2 ) (1,1,e^{-2}) (1,1,e−2)处取得极值另一个为( ( − 1 , − 1 , e − 2 ) (-1,-1,e^{-2}) (−1,−1,e−2)),则等值线 x y e − ( x 2 + y 2 ) = e − 2 xye^{-(x^2+y^2)}=e^{-2} xye−(x2+y2)=e−2 处的法向量为 ( − e − 2 , − e − 2 ) (-e^{-2},-e^{-2}) (−e−2,−e−2);且 x y − 1 = 0 xy-1=0 xy−1=0在 ( 1 , 1 ) (1,1) (1,1)处的法向量为 ( 1 , 1 ) (1,1) (1,1),显而可见两者平行。
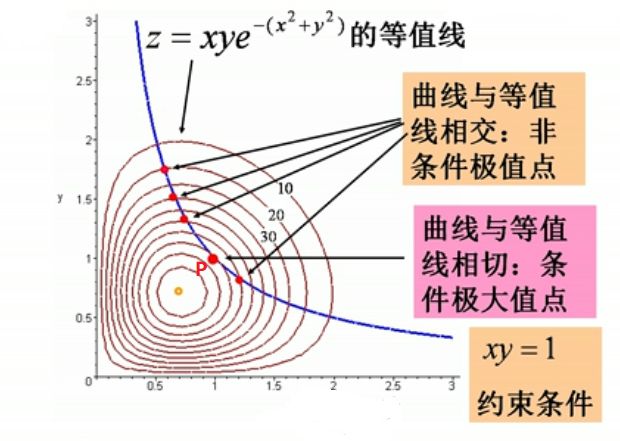
从等高线图来看:
总结一句话,拉格朗日乘除法就是根据在P点出两个法向量平行这个条件推导出来的。
感谢徐小湛老师的《高等数学》视频