SVM（一）：线性支持向量机

1.1 问题定义

（1） 划分超平面

二维样本空间中，划分平面可以表示为：$w_1{x}_1+w_2{x}_2+b=0$

在高维样本空间中，划分超平面定义如下：$${\mathbf{w}}^T\mathbf{x}+b=0$$
其中，$\mathbf{w}=(w_1,w_2,...,w_d)$为法向量，决定了超平面的方向；$b$为位移，决定了超平面与原点之间的距离。

设空间中任一点$\mathbf{x}$在超平面的投影为${\mathbf{x}}^{\prime }$，则$$\mathbf{x}=\mathbf{x}\prime +\lambda \mathbf{w}$$

$${\mathbf{w}}^T\mathbf{x}+b={\mathbf{w}}^T({\mathbf{x}}^{\prime }+\lambda w)+b={\mathbf{w}}^T{\mathbf{x}}^{\prime }+b+\lambda \mathbf{w}{\mathbf{w}}^T=\lambda {\mathbf{w}}^T\mathbf{w}$$

（2） 点到超平面的距离

样本空间中任意点$\mathbf{x}$到超平面的距离为
$$\begin{array}{rl}\gamma & =||\mathbf{x}-{\mathbf{x}}^{\prime }||\\ & =||\lambda \mathbf{w}||\\ & =\frac{\lambda {||\mathbf{w}||}^2}{||\mathbf{w}||}\\ & =\frac{|{\mathbf{w}}^T\mathbf{x}+b|}{||\mathbf{w}||}\end{array}$$

其中，$\left|\left|\mathbf{w}\right|\right|=\sqrt{{\sum }_{i=1}^n{w}_i^2}$为$w$的L2范数。

（3）支持向量、间隔

假设超平面能将训练样本正确分类，即对于$({\mathbf{x}}_i,y_i)\in D$，
$$\{\begin{array}{ll}{\mathbf{w}}^T{\mathbf{x}}_i+b>0,y_i=+1& \\ {\mathbf{w}}^T{\mathbf{x}}_i+b<0,y_i=-1& \end{array}$$

$$\begin{array}{rl}& \iff y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)>0\\ & \iff \exists r>0,s.t.\min y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)=r\end{array}$$

由于$\mathbf{w}与b$可任意缩放，令$r=1$
$$\begin{array}{rl}& \iff y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1\\ & \\ & \iff \{\begin{array}{ll}{\mathbf{w}}^T{\mathbf{x}}_i+b\ge +1,y_i=+1& \\ {\mathbf{w}}^T{\mathbf{x}}_i+b\le -1,y_i=-1& \end{array}\end{array}$$

如下图所示，距离超平面最近的训练样本点是得上式等号成立，称为支持向量（Support vector）。

支持向量到超平面的距离之和为$\gamma =\frac{2}{||\mathbf{w}||}$，称为间隔（margin）。

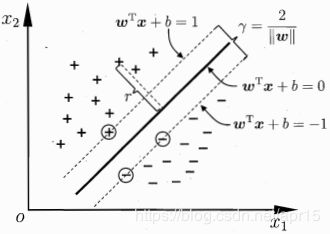
（4）最优超平面

能将两类样本划分的超平面有无数多个，具有最大分类间隔的超平面，称为最优超平面。
为找到具有最大间隔的划分超平面，需要$$\underset{\mathbf{w},b}{\max }\frac{1}{||\mathbf{w}||}s.t.y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1(i=1,2,...m)$$

即$$\underset{\mathbf{w},b}{\min }\frac{1}{2}||\mathbf{w}|{|}^{2}s.t.y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1(i=1,2,...m)$$

1.2 对偶问题

目标函数$\frac{1}{2}||\mathbf{w}|{|}_2^2$是凸函数，同时约束条件不等式是仿射的，是一个凸二次规划（convex quadratic programming）问题，可以用优化计算包求解（适用于维度较低的情况）。

另一种更高效的办法是，通过拉格朗日函数（对每条约束添加拉格朗日乘子${\alpha }_i\ge 0$）将的优化目标转化为无约束的优化函数:$$L(\mathbf{w},b,\mathbf{\alpha })=\frac{1}{2}||\mathbf{w}|{|}^2+\sum _{i=1}^m{\alpha }_i[1-y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)]\text{\hspace{1em}(1)}$$其中$\mathbf{\alpha }=({\alpha }_1,{\alpha }_2,...,{\alpha }_m)$

由于引入了朗格朗日乘子，优化目标变成：$$\underset{\mathbf{w},b}{\min }\underset{{\alpha }_i\ge 0}{\max }L(\mathbf{w},b,\mathbf{\alpha })\text{\hspace{1em}(2)}$$

该优化函数满足满足KTT条件，即
$$\{\begin{array}{l}{\alpha }_i\ge 0\\ \\ 1-y_{i}f({\mathbf{x}}_i)\le 0\\ \\ {\alpha }_i(y_{i}f({\mathbf{x}}_i)-1)=0\end{array}f({\mathbf{x}}_i)={\mathbf{w}}^T{\mathbf{x}}_i+b\text{\hspace{1em}(3)}$$

对于任意训练样本$({\mathbf{x}}_i,y_i)$，必有${\alpha }_i=0$或$y_{i}f({\mathbf{x}}_i)=1$。
若${\alpha }_i=0$，则该样本不会在求和式中出现，也就不会对$f(\mathbf{x})$有任何影响；
若${\alpha }_i>0$，则必有$y_{i}f({\mathbf{x}}_i)=1$，该样本点在最大间隔边界上，是一个支持向量。

这显示出支持向量基的一个重要性质：最终模型仅与支持向量有关

因此，根据拉格朗日对偶条件，原问题的对偶问题如下：

$$\underset{{\alpha }_i\ge 0}{\max }\underset{\mathbf{w},b}{\min }L(\mathbf{w},b,\mathbf{\alpha })\text{\hspace{1em}(4)}$$

极大极小问题：先求优化函数对于$w$和$b$的极小值，再求拉格朗日乘子$\alpha$的极大值

$L(\mathbf{w},b,\mathbf{\alpha })$关于$\mathbf{w}$和$b$极小值可以通过对$\mathbf{w}$和$b$分别求偏导得到：
$$\frac{\partial L}{\partial \mathbf{w}}=0\Rightarrow \mathbf{w}=\sum _{i=1}^m{\alpha }_i{y}_i{\mathbf{x}}_i\text{\hspace{1em}(5)}$$$$\frac{\partial L}{\partial b}=0\Rightarrow \sum _{i=1}^m{\alpha }_i{y}_i=0\text{\hspace{1em}(6)}$$将$w$的值代入$L(\mathbf{w},b,\mathbf{\alpha })$：

$$\begin{array}{rl}\underset{w,b}{\min }L(\mathbf{w},b,\mathbf{\alpha })& =\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{\mathbf{x}}_i^T{\mathbf{x}}_j\\ s.t.& \sum _{i=1}^m{\alpha }_i{y}_i=0,\\ & {\alpha }_i\ge 0,i=1,2,...m\end{array}\text{\hspace{1em}(7)}$$

原问题最终转换为如下形式的对偶问题：
$$\underset{{\alpha }_i\ge 0}{\max }\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{\mathbf{x}}_i^T{\mathbf{x}}_j\text{\hspace{1em}(8)}$$$$s.t.\begin{array}{rl}& \\ & \sum _{i=1}^m{\alpha }_i{y}_i=0,\\ & {\alpha }_i\ge 0,i=1,2,...m\end{array}$$此时，优化函数仅有$\mathbf{\alpha }$做为参数，可采用SMO（Sequential Minimal Optimization）求解。

1.3 问题求解

SMO算法则采用了一种启发式的方法，它每次只优化两个变量，将其他的变量都视为常数，将复杂的优化算法转化为一个简单的两变量优化问题.

由于$\sum _{i=1}^m{\alpha }_i{y}_i=0$.假如将${\alpha }_3,{\alpha }_4,...,{\alpha }_m$固定，那么${\alpha }_1,{\alpha }_2$之间的关系也确定了。初始化参数后，SMO不断执行以下两个步骤直至收敛：

• 选取一对需更新的变量${\alpha }_i$和${\alpha }_j$；
• 固定${\alpha }_i$和${\alpha }_j$以外的参数，求解获得更新后的${\alpha }_i$和${\alpha }_j$。

解出最优化对应的$\mathbf{\alpha }$的值${\mathbf{\alpha }}^{\ast }$后，可求出$$w^{\ast }=\sum _{i=1}^m{\alpha }_i^{\ast }{y}_i{\mathbf{x}}_i$$

对于任意支持向量$({\mathbf{x}}_s,y_s)$都有$y_{s}f({\mathbf{x}}_s)=1$，即$$y_s(\sum _{i\in S}{\alpha }_i{y}_i{\mathbf{x}}_i^T{\mathbf{x}}_s+b)=1$$

$S$为所有支持向量的集合，即满足${\alpha }_s>0$对应的样本$({\mathbf{x}}_s,y_s)$，理论上可任意选取支持向量通过上式，求得$b$。

一般采取一种更为鲁棒的方法，即计算出每个支持向量$({\mathbf{x}}_s,y_s)$对应的$b_s^{\ast }$，对其求平均值得到

$$b^{\ast }=\frac{1}{S}\sum _{i=1}^S(\frac{1}{y_s}-\sum _{i\in S}{\alpha }_i{y}_i{\mathbf{x}}_i^T{\mathbf{x}}_s)$$

最终得到分类超平面${\mathbf{w}}^{\ast T}\mathbf{x}+b^{\ast }=0$，分类决策函数为 $f(\mathbf{x})=sign({\mathbf{w}}^{\ast T}\mathbf{x}+b^{\ast })$