机器学习系列 04：梯度下降法及 Python 实现

  本内容将介绍 梯度下降法 以及其三种类型（ 批量梯度下降法（BGD）、随机梯度下降法（SGD） 和 小批量梯度下降法（MBGD））。最后将给出使用随机梯度下降法拟合一个线性回归模型的 Python 代码。

  在机器学习中，为了学得一个能够较好反映实际的模型，通常的方法：针对模型构建损失函数，然后使得损失函数最小化。在实际任务中，梯度下降法 是使用较多的一种方法。

一、梯度下降法

  梯度下降法（Gradient descent）是一个一阶最优化算法，是求解无约束最优化问题的常用算法，通常也称为最速下降法。要使用梯度下降法找一个函数的局部极小值，必须向函数上当前点对应梯度的反方向的规定步长距离点进行迭代搜索。如果相反地向梯度正方向迭代进行搜索，则会接近函数的局部极大值，这个过程被称为梯度上升法。

  更直观的理解：比如当前我们站在山上的某一点，环顾四周找到最陡的一个坡，沿此方向向下走一步；走到新的点后，再找到最陡的坡，向下走一步，按照此方法不断的往下走，直到走到“最低点”。

  假设损失函数为 $E(w)$，则参数 $w$ 的更新迭代公式为

$$\hat{w}=w-\eta \nabla E(w)\text{\hspace{1em}(1)}$$

其中，$\hat{w}$ 表示新求得的参数 $w$（与原来的 $w$ 进行区别），$\eta$ 为学习速率，$\nabla E(w)$ 表示 $E(w)$ 的梯度。

  在实际任务中，使用梯度下降法的流程如下：

• 首先对参数 $w$ 进行随机初始化，一般初始化为一个全零向量。
• 然后不断采用式（1）迭代更新参数 $w$，直到收敛或者达到设定的迭代次数。

  下面我们用线性回归模型来具体说明实际使用梯度下降法的过程。假设需要拟合的函数 $f_w(x)$ 为线性回归模型（如果不理解线性回归模型，可以参阅这里），即

$$f_w(x)=w_0{x}_0+w_1{x}_1+\cdots +w_n{x}_n=\sum _{j=0}^n{w}_j{x}_j\text{\hspace{1em}(2)}$$

其中，$n$ 为特征数量，$x_j$ 为特征值，$x_0=1$，$w_j$ 为需要求得的参数。损失函数 $E(w)$ 为平方损失函数，即

$$E(w)=\frac{1}{2m}\sum _{i=1}^m(f_w(x^{(i)})-y^{(i)}{)}^2\text{\hspace{1em}(3)}$$

其中，$m$ 为样本数量。这里乘以 $\frac{1}{2}$ 是为了后面计算更加方便，实际上是否乘以 $\frac{1}{2}$ ，对最终的最优解都不会产生影响。

  对 $E(w)$ 中的每个 $w_j$ 求偏导数（即梯度），得到

$$\nabla E(w_j)=\frac{\partial E(w)}{\partial w_j}=\frac{\partial }{\partial w_j}\frac{1}{2m}\sum _{i=1}^m(f_w(x^{(i)})-y^{(i)}{)}^2$$

$$=\frac{1}{2m}\sum _{i=1}^m\frac{\partial }{\partial w_j}(f_w(x^{(i)})-y^{(i)}{)}^2$$

$$=\frac{1}{2m}\sum _{i=1}^{m}2(f_w(x^{(i)})-y^{(i)})\frac{\partial }{\partial w_j}(f_w(x^{(i)})-y^{(i)})$$

$$=\frac{1}{m}\sum _{i=1}^m(f_w(x^{(i)})-y^{(i)})x_j^i\text{\hspace{1em}(4)}$$

  根据式（1）和式（4）可知，参数 $w_j$ 的迭代更新公式为

$$\widehat{w_j}=w_j-\eta \frac{1}{m}\sum _{i=1}^m(f_w(x^{(i)})-y^{(i)})x_j^i\text{\hspace{1em}(5)}$$

其中，$\eta$ 为学习速率。

  通过式（5）不断地迭代更新参数 $w$，将获得 $w$ 的最优解或者最优解附近的值。

二、梯度下降法的种类

  根据式（5）中的 $m$ 取值（即选择的样本数量）的不同，梯度下降法分为 批量梯度下降法（BGD）、随机梯度下降法（SGD） 和 小批量梯度下降法（MBGD）。

2.1 批量梯度下降法

  当 $m$ 为测试集中全部样本数量时，称为 批量梯度下降法（Batch Gradient Descent，BGD）。从式（5）可以看到，每迭代一次，会用到训练集中的所有样本，这样可以得到一个全局最优解；但是当 $m$ 很大时，计算量将会很大，迭代的速度会比较慢。

2.2 随机梯度下降法

  当 $m$ 为 1 时（即每次只选择一个样本），称为 随机梯度下降法（Stochastic Gradient Descent，SGD）。即每次只选择一个样本来迭代更新参数 $w$，在样本数量很大的情况下，可能只需要用到一部分样本就可以求得参数 $w$ 的最优解。因此随机梯度下降法相比批量梯度下降法，在计算量上会大大减少。

  当然，随机梯度下降法同样也存在一些缺点：相比批量梯度下降法，其噪音比较多；因此随机梯度下降法每次迭代时，并不都是向着整体最优化方向更新。但是大的整体方向是向着最优解的。

2.3 小批量梯度下降法

  当 $m$ 为远小于测试集中全部样本数量并且大于 1 时，称为 小批量梯度下降法（mini-batch Gradient Descent，MBGD）。比如测试集中全部样本数量为 10000，$m$ 为 20。在实际任务中，通常使用交叉验证法来选取 $m$。

总结：当测试集中样本数量比较少时，我们完全可以使用批量梯度下降法来迭代更新参数 $w$。但是当样本数量比较多时，我们可以选择使用随机梯度下降法或者小批量梯度下降法。

2.4 代码实现

  下面是使用随机梯度下降法拟合一个线性回归模型的代码（Python 3.x）：

import matplotlib.pyplot as plt
import numpy as np


class LinearRegression:
    """
    初始化线性回归模型，并初始化权值（weights）和偏置（bias）。

    feature_num：feature 数量
    """
    def __init__(self, feature_num):
        self.feature_num = feature_num
        self.weights = np.zeros(feature_num)

    def __str__(self):
        return 'Weights: %s\n' % self.weights

    """
    进行模型训练

    features：训练数据中的特征值（格式：（x0, x1, ... xn））
    labels：训练数据中的标签值
    learning_rate：学习速率
    threshold_values：损失阈值
    """
    def train(self, features, labels, learning_rate, threshold_value):
        cost01 = 0.0
        # 迭代更新参数 weights
        while True:
            for i in range(len(features)):
                # 每次使用一个样本更新参数 weights，即 SGD
                output = self.predict(features[i])
                delta = output - labels[i]
                # 梯度为 delta * features[i][j]
                for j in range(self.feature_num):
                    self.weights[j] -= learning_rate * delta * features[i][j]

            # 计算损失
            cost02 = 0.0
            for i in range(len(features)):
                cost02 += self.predict(features[i])

            # 当前后两次的损失小于设定的阈值时，停止训练
            if abs(cost02 - cost01) < threshold_value:
                break
            else:
                cost01 = cost02

    """
    进行预测
    """
    def predict(self, feature):
        return np.dot(feature, self.weights)


def get_training_data():
    x = [(1., 1.), (1., 2.), (1., 4.5), (1., 5.), (1., 9.), (1., 11.)]
    y = [5, 6, 12, 14, 21.5, 25]
    return x, y


if __name__ == "__main__":
    linear_regression = LinearRegression(2)
    features, labels = get_training_data()
    linear_regression.train(features, labels, 0.01, 0.0001)
    print(linear_regression)

    # 绘图
    xArr = [x[1] for x in features]
    yArr = [linear_regression.predict(x) for x in features]
    plt.plot(xArr, labels, 'bx', xArr, yArr, 'r')
    plt.show()

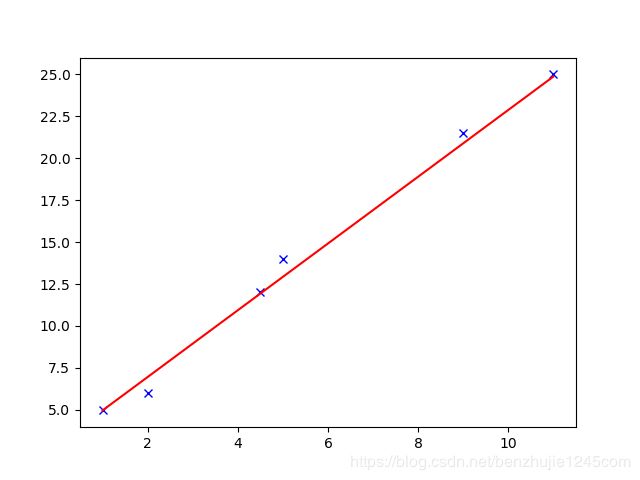
运行以上代码后，将打印如下信息及如下图形：

Weights: [2.97224167 1.99106495]

参考：
[1] https://zh.wikipedia.org/wiki/梯度下降法
[2] https://blog.csdn.net/cs24k1993/article/details/79120579
[3] https://blog.csdn.net/yhao2014/article/details/51554910