数据结构——二叉树知识总结

  

  二叉树不是树的一种特殊情形,尽管其与树有许多相似之处,但树和二叉树有两个主要差别:

树中结点的最大度数没有限制,而二叉树结点的最大度数为2;

树的结点无左、右之分,而二叉树的结点有左、右之分。

一、二叉树的逻辑结构

1、二叉树的定义

二叉树是n（n≥0）个结点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树的二叉树组成。

2、二叉树的特点：

⑴ 每个结点最多有两棵子树；

⑵ 二叉树是有序的，其次序不能任意颠倒。

3、特殊的二叉树

斜树

所有结点都只有左子树的二叉树称为左斜树；

所有结点都只有右子树的二叉树称为右斜树；

3.左斜树和右斜树统称为斜树。

斜树的特点：

在斜树中，每一层只有一个结点；

斜树的结点个数与其深度相同。

满二叉树

在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且所有叶子都在同一层上。

满二叉树的特点：

叶子只能出现在最下一层；

只有度为0和度为2的结点。

满二叉树在同样深度的二叉树中结点个数最多

满二叉树在同样深度的二叉树中叶子结点个数最多

完全二叉树

对一棵具有n个结点的二叉树按层序编号，如果编号为i（1≤i≤n）的结点与同样深度的满二叉树中编号为i的结点在二叉树中的位置完全相同。

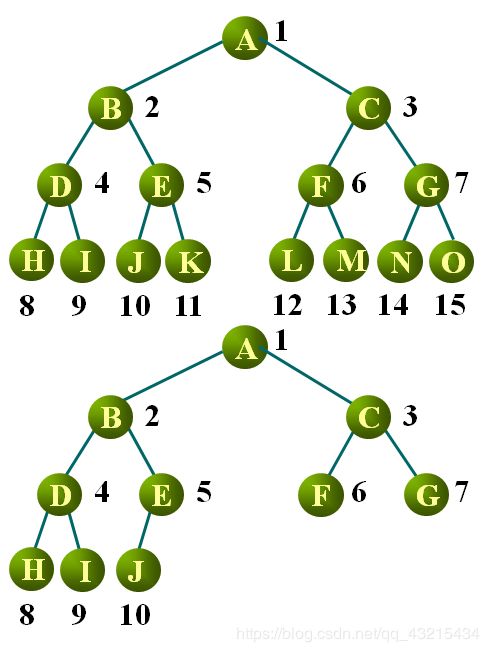在满二叉树中，从最后一个结点开始，连续去掉任意个结点，即是一棵完全二叉树。

完全二叉树的特点：

 叶子结点只能出现在最下两层，且最下层的叶子结点都集中在二叉树的左部；

完全二叉树中如果有度为1的结点，只可能有一个，且该结点只有左孩子。

深度为k的完全二叉树在k-1层上一定是满二叉树。

4、二叉树的基本性质

（1）二叉树的第i层上最多有2i-1个结点（i≥1）。

（2）棵深度为k的二叉树中，最多有2k-1个结点，最少有k个结点。

（深度为k且具有2k-1个结点的二叉树一定是满二叉树，

深度为k且具有k个结点的二叉树不一定是斜树。）

（3）在一棵二叉树中，如果叶子结点数为n0，度为2的结点数为n2，则有: n0＝n2＋1。

（4）的完全二叉树的深度为 log2n  +1。

（5）对一棵具有n个结点的完全二叉树中从1开始按层序编号，则对于任意的序号为i（1≤i≤n）的结点（简称为结点i），有：

①

如果i＞1，则结点i的双亲结点的序号为  i/2；

如果i＝1，则结点i是根结点，无双亲结点。

②

如果2i≤n，则结点i的左孩子的序号为2i；

如果2i＞n，则结点i无左孩子。

③

如果2i＋1≤n，则结点i的右孩子的序号为2i＋1；

如果2i＋1＞n，则结点 i无右孩子。

对一棵具有n个结点的完全二叉树中从1开始按层序编号，则

结点 i的双亲结点为   i/2；

结点 i的左孩子为2 i；

结点i的右孩子为2i＋1。

5、二叉树的抽象数据类型定义

ADT BiTree

Data

    由一个根结点和两棵互不相交的左右子树构成，

    结点具有相同数据类型及层次关系

Operation

   InitBiTree

      前置条件：无

      输入：无

      功能：初始化一棵二叉树

      输出：无

      后置条件：构造一个空的二叉树

DestroyBiTree

       前置条件：二叉树已存在

       输入：无

       功能：销毁一棵二叉树

       输出：无

       后置条件：释放二叉树占用的存储空间 

InsertL

      前置条件：二叉树已存在

      输入：数据值x，指针parent

      功能：将数据域为x的结点插入到二叉树中，作为结点parent的左孩子。如果结点parent原来有左孩子，则将结点parent原来的左孩子作为结点x的左孩子

      输出：无

      后置条件：如果插入成功，得到一个新的二叉树   

DeleteL

     前置条件：二叉树已存在

     输入：指针parent

     功能：在二叉树中删除结点parent的左子树

     输出：无

     后置条件：如果删除成功，得到一个新的二叉树

Search

      前置条件：二叉树已存在

      输入：数据值x

      功能：在二叉树中查找数据元素x

      输出：指向该元素结点的指针

      后置条件：二叉树不变  

PreOrder

前置条件：二叉树已存在

输入：无

功能：前序遍历二叉树

输出：二叉树中结点的一个线性排列

后置条件：二叉树不变

InOrder 

前置条件：二叉树已存在

输入：无

功能：中序遍历二叉树

输出：二叉树中结点的一个线性排列

        后置条件：二叉树不变

PostOrder

      前置条件：二叉树已存在

      输入：无

      功能：后序遍历二叉树

      输出：二叉树中结点的一个线性排列

      后置条件：二叉树不变   

LeverOrder

      前置条件：二叉树已存在

      输入：无

      功能：层序遍历二叉树

      输出：二叉树中结点的一个线性排列

      后置条件：二叉树不变

endADT

6、二叉树的遍历操作

前序：DLR

中序：LDR

后序：LRD

层序遍历：按二叉树的层序编号的次序访问各结点。

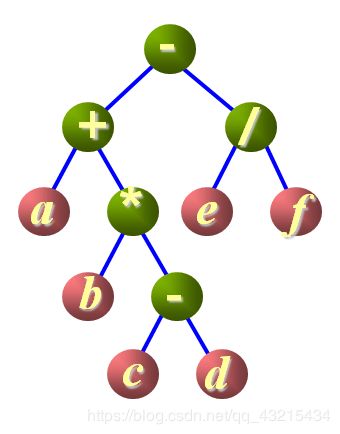
前序遍历结果：- + a * b - c d / e f

中序遍历结果：a + b * c - d - e / f后序遍历结果：a b c d - * + e f / -

二、二叉树的存储结构及实现

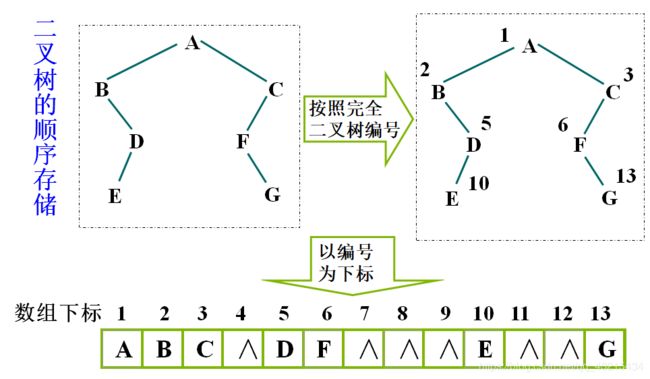
1、顺序存储结构

二叉树的顺序存储结构就是用一维数组存储二叉树中的结点，并且结点的存储位置（下标）应能体现结点之间的逻辑关系——父子关系。

遍历：

void Preorder(int root, char data[]){

  if(data[root]!='\0'){

  cout<

  Preorder(2*root,data);

  Preorder(2*root+1,data);

}

  return;

}

void InOrder(int root, char data[]){

  if(data[root]!='\0'){

  InOrder(2*root,data);

  cout<

   InOrder(2*root+1,data); 

  }

  return;

}

void PostOrder(int root, char data[]){

  if(data[root]!='\0'){

   PostOrder(2*root,data);

   PostOrder(2*root+1,data);

  cout<

  }

  return;

}

 

void create(char preorder[],char inorder[],int start_p, int end_p,int start_i,int end_i, char data[],int root){

  if(start_p>end_p)

  return ;

  else{

  int k;

  for(int i=start_i;i<=end_i;i++){

  if(inorder[i]==preorder[start_p]){

  k=i;

  break;

  }

  }

  data[root]=preorder[start_p];

  create(preorder,inorder,start_p+1,start_p+k-start_i,start_i,k-1,data, 2*root);

  create(preorder,inorder,start_p+k-start_i+1,end_p,k+1,end_i,data,2*root+1);

  }

  return ;

}

int main(){  

    char * data;

  int total=1;

  char preorder[100],inorder[100];

  cin>>preorder>>inorder;

  int length=0;

  while(preorder[length]!='\0')

  length++;

  data=new char[pow(2,length+1)];

  memset(data,'\0',pow(2,length+1));

  create(preorder,inorder,0,length-1,0,length-1,data,1);

  order(1,data);

  return 0;

}

2、二叉链表

基本思想：令二叉树的每个结点对应一个链表结点，链表结点除了存放与二叉树结点有关的数据信息外，还要设置指示左右孩子的指针。

其中，data：数据域，存放该结点的数据信息；

            lchild：左指针域，存放指向左孩子的指针；

            rchild：右指针域，存放指向右孩子的指针。

template

struct BiNode

{

    T data;

    BiNode *lchild, *rchild;

};

具有n个结点的二叉链表中，有n+1个空指针

3、二叉链表的存储结构的类声明

template

class BiTree

{   

  public:

       BiTree();

        ~BiTree( );           

        void PreOrder(){PreOrder(root);}

        void InOrder() {InOrder(root);}

        void PostOrder() {PostOrder(root);}

        void LevelOrder(){LeverOrder(root)};

  private:

        BiNode *root;

        BiNode * Creat( );

        void Release(BiNode *root);

        void PreOrder(BiNode *root);

        void InOrder(BiNode *root);

        void PostOrder(BiNode *root);

        void LevelOrder(BiNode *root);

 };
 

4、二叉树的建立

1.按前序扩展遍历序列输入输入节点的值

2.如果输入节点之为“#”,则建立一棵空的子树

3.否则，根结点申请空间，将输入值写入数据域中，

4.以相同方法的创建根节点的左子树

5.以相同的方法创建根节点的右子树

template

class BiTree{

public:

       BiTree();

        ~BiTree( );           

        void PreOrder(){PreOrder(root);}

        void InOrder() {InOrder(root);}

        void PostOrder() {PostOrder(root);}

        void LevelOrder();

  private:

        BiNode *root;

        void Creat(BiNode *& root);

        void Release(BiNode *root);

        void PreOrder(BiNode *root);

        void InOrder(BiNode *root);

        void PostOrder(BiNode *root);

        void LevelOrder(BiNode *root);

};

template

BiTree::BiTree( )

{

  Creat(root);

}

template

void BiTree::Creat(BiNode * &root  )

{

      T ch;

      cout<<"请输入创建一棵二叉树的结点数据"<

      cin>>ch;

         if (ch=="#") root = NULL;

         else{

             root = new BiNode;       //生成一个结点

                root->data=ch;

               Creat(root->lchild );    //递归建立左子树

               Creat(root->rchild);    //递归建立右子树

    }

}

template  

void   BiTree::PreOrder(BiNode *root)

{

        if (root ==NULL)  return;    

        else {

            cout<data;        

            PreOrder(root->lchild);   

            PreOrder(root->rchild);   

        }

 }

template

void BiTree::InOrder (BiNode *root)

{

         if (root==NULL) return;    

         else {

               InOrder(root->lchild);

               cout<data;

               InOrder(root->rchild);

         }

}

template

void BiTree::PostOrder (BiNode *root)

{

         if (root==NULL) return;    

         else {

               PostOrder (root->lchild);

               PostOrder (root->rchild);

               cout<data;

         }

}

 5、层序遍历

1.队列Q初始化；

2. 如果二叉树非空，将根指针入队；

3. 循环直到队列Q为空

      3.1 q=队列Q的队头元素出队；

      3.2 访问结点q的数据域；

      3.3 若结点q存在左孩子，则将左孩子指 针入队；

      3.4 若结点q存在右孩子，则将右孩子指针入队；

using namespace std;

template

void BiTree::LevelOrder(BinaryTreeNode* root){

  queue*> aQueue;

  if(root)

  aQueue.push(root);

//首先创建一个空队列；判断根节点是否为空，如果不空，根节点入队

  while(!aQueue.empty())

{

  root=aQueue.front(); //取队列首结点

  aQueue.pop();

  cout<data;//访问当前结点

  if(root->lchild)  //左子树进队列

  aQueue.push(root->lchild);

  if(root->rchild) //右子树进队列

  aQueue.push(root->rchild);  

  }//end while

}

1.队首出队（P），输出队首的值，将P的所有孩子（非0）入队

2.重复第二步的工作，直到队空

6、二叉树的析构

template

void BiTree::Release(BiNode* root){

  if (root != NULL){                 

      Release(root->lchild);   //释放左子树

      Release(root->rchild);   //释放右子树

      delete root;

  } 

}

template

BiTree::~BiTree(void)

{

  Release(root);

}

7、设计算法求二叉树的结点个数。

void Count(BiNode *root){

    if (root) {

         Count(root->lchild);

         number+ +;  //number为数据成员

         Count(root->rchild);

   }

}

8、统计叶子节点的数目

template

int BiTree::count(BiNode* root){

  int number=0;

 

  if (root==NULL)

  number=0;

  else

  number=count(root->lchild)+count(root->rchild)+1;

  return number;

}

9、计算树的高度

template

 int BiTree::cal_height(BiTreeNode * root){

  int lheight=0,rheight=0;

  if (root==0)     return 0; 

  lheight=cal_height(root->lchild);

  rheight=cal_height(root->rchild);

  if (lheight>rheight)  return lheight+1;

  else   return rheight+1;

}