数据结构（十六） -- C语言版 -- 树 - 二叉树的线索化及遍历 -- 左指针域线索化、顺序表线索化、链表线索化

  推荐大佬的内容，有兴趣的小伙伴可以去观摩观摩哦！真心很不错的呢，我也在学习中的哟！

Python数据分析与挖掘

零、读前说明

• 本文中所有设计的代码均通过测试，并且在功能性方面均实现应有的功能。
• 设计的代码并非全部公开，部分无关紧要代码并没有贴出来。
• 如果你也对此感兴趣、也想测试源码的话，可以私聊我，非常欢迎一起探讨学习。
• 由于时间、水平、精力有限，文中难免会出现不准确、甚至错误的地方，也很欢迎大佬看见的话批评指正。
• 嘻嘻。。。。 。。。。。。。。收！

一、什么是线索化、什么是线索二叉树

  线索：将二叉链表中的 空指针域 指向其在某种遍历次序（如先序、中序、后序或层次等）下该节点的 前驱节点 和 后继节点 的 指针 ，这些指针称为线索。

  线索化：在对二叉树以某种遍历次序（如先序、中序、后序或层次等）进行遍历的过程中使其节点的 空指针域指向其前驱节点或者后继节点的信息的过程 称为对二叉树进行线索化，也就是把二叉树变为线索二叉树的过程。

  线索链表：在二叉链表的节点上加上线索的二叉链表称为线索链表。

  线索二叉树：在二叉树的节点上加上线索的二叉树称为线索二叉树。

二、为什么要进行线索化二叉树

  当然是因为有需要了！！！！

  1、从占用内存方面考虑，可以发现在二叉链表表示的树的结构中，并不是每一个节点都能充分利用指针域，并且叶子节点直接空了两个指针域，所以，在这种情况下，如果一个二叉树节点比较多的话，那么叶子节点也会同步增多，那对于内存的浪费就会比较严重。

  比如说：对于一个个有 n 个节点的二叉链表， 每个节点有指向左右孩子的两个指针域，所以共是 2n 个指针域。而 n 个节点的二叉树一共有 n-1 条分支数，也就是说，其实是存在 2n-(n-1) = n+l 个空指针域，可见空间浪费比较严重。（摘自《大话数据结构》 P189 ）

  2、对于一些需要频繁进行二叉树遍历操作的场合，二叉树的非递归遍历操作过程相对比较复杂，递归遍历虽然简单明了，但是会有额外的开销，对于操作的时间和空间都比较浪费。

  3、在任何一种遍历中，都会得到了节点特定的序列，可以很清楚的看到任意一个节点的前驱节点和后继节点。但是在用二叉链表表示的树的结构中，并没有节点的前驱或者后继节点的信息，那么如需要查找某个节点的的前驱或者后继节点的时候，我们需要再重新进行一次遍历，节点少还好，万一节点很多哪。。。

  所以，为了各方面的考虑，在创建树的时候就记录节点的前驱和后继节点，那么是不是后面需要的时候就很愉快的满足呢。。。。

  综上所述：线索化二叉树的目的就是将非线性的结构的节点用线性的形式去去访问，也就是用链表或者顺序表的方式的进行二叉树节点的访问

  1、在链表中， 节点的先后顺序是没有什么实际意义的，但是在二叉树中，节点的先后顺序一般表示了其左右子树的关系
  2、线索化二叉树是将二叉树中的节点进行逻辑意义上的“重排列”，使其可以线性的方式访问每一个节点
  3、二叉树线索化之后每个节点都是一个线性下标，通过这个下标可以快速访问节点而不需要遍历二叉树

  二叉树的遍历有四种形式，所以就会有四种意义下的前驱节点和后继节点，相应的就有四种线索二叉树：

先序线索二叉树 中序线索二叉树 后序线索二叉树 层序线索二叉树   

  所以，对于下面提到的任何一种线索化的过程，均会有上面四种遍历顺序的对应的实现方式，其实对于每一种线索化的过程，其四种实现方式均大同小异，所以本文只提到详细说明其中一种线索化的遍历过程，对应的其他的方式可以自行按照遍历的过程进行研究。

三、线索化二叉树及其遍历

  以下面这个二叉树为例进行先序线索化的过程说明以及演示，其二叉链表的表示方法为右边图这样( ^ 表示为空)。
  

图3.1 二叉树以及二叉链表表示示意图

  
  为了方便下面的分析，首先根据上图中的树的结构形状，其四种遍历的结果为：

先序： A->B->D->G->E->C->F 中序： D->G->B->E->A->F->C 后序： G->D->E->B->F->C->A 层序： A->B->C->D->E->F->G   

  下面就一先序遍历的顺序进行先序线索化的说明。

3.1、利用空指针域线索化二叉树及其遍历 — 先序线索化

3.1.1、线索化分析说明

  前面已经提到。对于一个有 n 个节点的二叉链表，是存在 2n-(n-1) = n+l 个空指针域。那么可以利用二叉链表节点中的 空指针域，使其指向 后继节点 来线索化二叉树。

  由上图3.1中表示，节点 A、B 的左右孩子指针均已经被占用，节点 C、D 左孩子或者右孩子其中一个被占用，另一个为空，叶子节点 G、E、F 左右孩子指针均为空。

  根据先序遍历结果 A->B->D->G->E->C->F ，在访问过程中，首先需要访问 根节点，然后 左子树，然后再 右子树 依次进行访问。那么在此模式下进行线索化，我们可以将 每个节点的左指针域指向其后继节点。这样在访问的过程一直判断节点的 左指针域 即可完成二叉树节点的访问。

  所以，将二叉树进行先序线索化的效果如下图所示。
  

图3.2 二叉树线索化表示示意图   

  将上面图中的二叉树按照左指针依次进行访问（按照顺序 1、2、3、4、5、6、7 ），此时，顺序正好与先序遍历的结果相同。

  下面就进行分析一下，如何在先序遍历的过程中实现线索化。

  1、在进行遍历根节点 A 的时候，其左孩子和右孩子均存在，所以按照先序遍历的顺序，需要继续遍历访问其左孩子，此时存在左孩子满足线性的条件，也就是 A 的后继节点为 B 。

  2、遍历节点 A 的左子树（节点 B ）的时候，同样节点 B 存在左右孩子，操作方法与根节点 A 一致。也就是 B 的后继节点为 D 。

  此时，显示效果如下图所示。
  

图3.3 二叉树线索化过程示意图1   

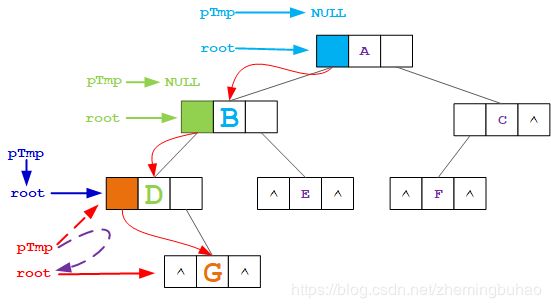
  3、在遍历节点 B 的左子树（节点 D ）的时候，此时节点 D 的左孩子为空，所以需要进行线索化的操作了，将节点 D 的左孩子指针指向其后继节点，根据先序遍历的顺序，此时需要判断右孩子了，可见存在右孩子节点 G ，所以遍历访问右孩子节点 G 。所以，节点 D 的后继节点为节点 G 。

  但是怎么将节点 G 和节点 D 的左指针域关联呢？

  我们需要一个辅助指针来保存左指针域为空的节点，假设定义为 pTmp 。

  那么在遍历节点 D 的时候，因为节点 D 的左孩子为空，所以我们需要给节点 D 的左指针域线索化成其后继节点，所以将辅助指针 pTmp 指向节点 D 。而其后继节点只能在接下来的遍历中获取了。

  4、遍历访问节点 D 的右子树（节点 G ），根据前面的说明我们已经清楚，节点 D 的左指针域需要线索化成节点 G ，但是代码应该怎么判断呢？

  有前面的节点 A ，节点 B 我们看出来，因为存在左孩子就没有提到到临时变量，但是在节点 D 的时候不存在左孩子反而需要保留节点 D 的值，所以，判断临时变量是否为空，应该可以实现判断是否需要将左指针域线索化。
  那么此时， pTmp 指向节点 D 并不为空，按照分析来说应该需要操作，那么操作的内容就是将 pTmp 的左指针域指向本节点（节点 G ），也就是 pTmp->lchild = root ，同时因为 pTmp 还用做了判断的条件，所以，在做完操作我们还需要清理当前的案发现场，也就是设置 pTmp = NULL 。

  但是根据上面的描述，在节点的左子树为空的时候，需要用 pTmp 来记录当前节点的值，以便于将应该的后继节点链接，所以， pTmp 又需要指向节点 G （当前节点 root ，下图中 pTmp 从 红色 变成 虚线紫色 ）。

  此时，显示效果如下图所示。

图3.4 二叉树线索化过程示意图2   

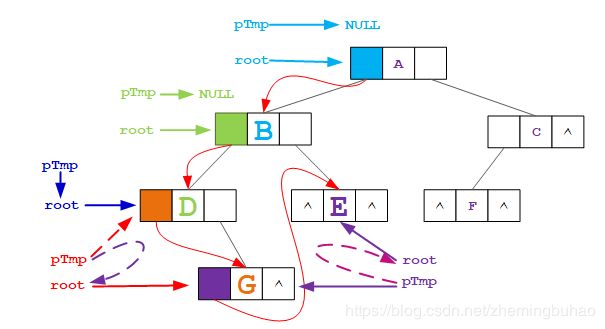
  5、按照先序遍历顺序，接下来需要遍历的是根节点 B 的右子树节点 E ，而节点 E 的情况与 G 一致，所以也没有什么例外的，根据上面描述，此时 pTmp 指向节点 G ，当前节点 root 指向节点 E ，所以，将 pTmp->lchild = E ，完成节点 G 的左指针域的线索化。
  并且节点 E 的左子树为空，所以 pTmp 又需要指向结点 E （当前节点 root ，下图中 pTmp 从 紫色 变成 虚线紫红色）。

  此时，显示效果如下图所示。

图3.5 二叉树线索化过程示意图3   

  6、接下来需要遍历的是根节点 A 的右子树节点 C ，而节点 C 存在左孩子，所以对于节点 C 来说不需要进行线索化，但是此时 pTmp 还是指向节点 E 并不为空，并且节点 E 的左孩子需要进行线索化为当前节点，所以在 pTmp 不为空的时候，需要更新 pTmp->lchild 的指向为当前节点（也即是将当前节点 C 线索化到前驱节点 E 的左指针域中），并且将 pTmp 重新指向 NULL （ pTmp 从 紫红色 变成 深蓝色 ）。并且当前节点的左子树不为空，所以继续遍历。

  7、接下来遍历的根节点 C 的左子树节点 F ，此时， pTmp 指向 NULL ，也就是当前节点F的前驱节点是确定的（节点 C ），但是当前节点 F 的左子树为空，所以 pTmp 重新指向当前节点 root ，以备链接器后继节点，但是其右子树也为空，所以此时所有节点均遍历完成，同时也完成了线索化。

  此时，显示效果如下图所示。

图3.6 二叉树线索化过程示意图4   

  此时，所有节点（除了节点 F ）的左指针域均指向其后继节点。我们已经可以按照 root->lchild 来完整的遍历整个树中的所有节点了。

  综上所述，程序算法的实现的过程大概可以描述为：

    初始化位置指针 pTmp= NULL
    先序遍历二叉树，然后判断 pTmp
    如果 pTmp 不为空，将 pTmp->lchild 指向 当前节点，并设置 pTmp = NULL
    如果 当前节点的左子树 为空，将 pTmp 指向 当前节点

3.1.2、线索化代码实现

  所以，实现的代码可以这样编写了。

/**
 *  功 能：
 *      线索化二叉树 -- 利用空左指针域
 *  参 数：
 *      root：要线索化的树的根节点
 *      ptmp：临时变量，用于保留前驱节点
 *  返回值：
 *      无
 **/
void thread_lchild(BiTNode *root, BiTNode **ptmp)
{
    if ((root != NULL) && (ptmp != NULL))
    {
        if (*ptmp != NULL)
        {
            (*ptmp)->lchild = root;
            *ptmp = NULL;
        }

        if (root->lchild == NULL)
        {
            *ptmp = root;
        }

        thread_lchild(root->lchild, ptmp);
        thread_lchild(root->rchild, ptmp);
    }
}

3.1.3、遍历线索化代码实现

  在前面的分析过程中，我们在线索化的过程已经将一个普普通通的二叉树线索化成了线索二叉树了。并且每个节点的左指针域均已经指向了其后继节点，那么他的遍历将是一个很简单的过程了，不就是一路 lchild ，直到 lchild = NULL 为止。

  所以，实现的代码可以这样编写了。

/**
 *  功 能：
 *      遍历利用空左指针域线索化二叉树 
 *  参 数：
 *      root：要遍历的线索二叉树的根节点
 *  返回值：
 *      无
 **/
void thread_lchild_print(BiTNode *root)
{
    while (root != NULL)
    {
        printf("%c ", root->data);
        root = root->lchild;
    }
    printf("\n");
}

  从上面的总结描述可以得知，在使用空指针域进行线索化的时候，会修改原本二叉树的节点之间的关系，所以在使用此方法线索化二叉树之后，此时二叉树已经不是原来的那个二叉树了。

  这个方法线索化后的二叉树在插入节点或者删除节点的是操作相对比较复杂。并且如果需要找到某一个节点的话，我们还是需要从头开始遍历每个节点。

  对于每一个节点，我们只能确定其后继节点，但是不能确定其前驱节点

  如果上面提到的有一条不能接受，那么就需要向其他办法，那么下面的方法可以尝试一下咯。。。

  此种线索化方式下的中序、后序等可以自行实现，此处不再赘述，实现过程一致。
  

3.2、利用线性表线索化二叉树及其遍历 — 先序线索化

3.2.1、线索化过程分析说明及代码实现

  利用线性表保存二叉树的遍历顺序，这里面也就可以使用顺序表、链表的方式来保存。首先用顺序表进行说明。

  利用线性表保存二叉树的遍历顺序，就是在原本的遍历树的基础上改进一下，将原来的打印的语句修改成线性表插入节点的语句就可以在便利的基础上完成线索化，并且，这种线索化的过程对原本的二叉树没有造成任何影响，二叉树还是原来的那个二叉树，从没有发生丝丝改变 ^ _ ^

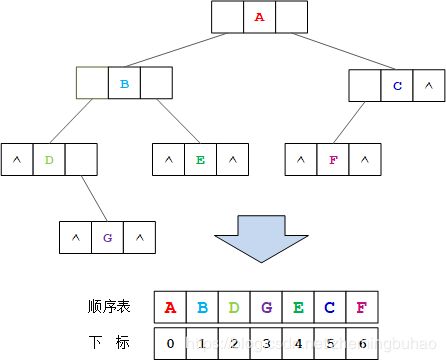
  对于每一个节点的前驱节点和后继节点的信息，按照下标的左右即可确定。十分快速方便的即可确定其前驱和后继。

  其中各个节点与顺序表中节点对应关系如下图所示。

图3.7 二叉树线索化过程对应关系示意图   

  综上所述，程序算法的实现的过程大概可以描述为：

  1、创建并初始化线性表
  2、先序遍历二叉树，在遍历过程中将当前节点插入到线性表中

  所以，实现的代码可以这样编写了。

/**
 *  功 能：
 *      线索化二叉树 -- 利用顺序表
 *  参 数：
 *      root：要线索化的树的根节点
 *      list：顺序表的操作句柄
 *  返回值：
 *      无
 **/
void thread_seqlist(BiTNode *root, seqList *list)
{
    if ((root != NULL) && (list != NULL))
    {
        fSeqList.insert(list, (ListNode *)root, fSeqList.length(list));

        thread_seqlist(root->lchild, list);
        thread_seqlist(root->rchild, list);
    }
}

3.2.2、遍历线索化代码实现

  在前面的分析过程中，我们已经将线索化的节点的信息保存在顺序表中了，那么遍历的话也就是 按照下标 一一进行访问即可。

  所以，实现的代码可以这样编写了。

/**
 *  功 能：
 *      遍历利用顺序表线索化二叉树
 *  参 数：
 *      list：顺序表的操作句柄
 *  返回值：
 *      无
 **/
void thread_seqlist_print(seqList *list)
{
    int i;
    for (i = 0; i < fSeqList.length(list); i++)
    {
        BiTNode *tmp = (BiTNode *)fSeqList.get(list, i);
        printf("%c ", tmp->data);
    }

    printf("\n");
}

  这种线索化方式，保留二叉树的结构与关系。需要遍历的时候直接访问顺序表，快速，方便，简单，可以十分方便的确定每个节点的前驱节点和后继节点。

  这个方法线索化后的二叉树在插入节点或者删除节点的是操作相对比较复杂，并且顺序表的容量扩展也比较麻烦。

  那么，从顺序表的优缺点和链表的比较来看， 我们也可以实现链表的线索化来比较。

  此种线索化方式下的中序、后序等可以自行实现，此处不再赘述。

3.3、利用链线索化二叉树及其遍历 — 先序线索化

3.3.1、线索化过程分析说明及代码实现

  这种线索化的方式与顺序表的线索化过程一致，就是在原本的遍历树的基础上改进一下，将原来的打印的语句修改成链表插入节点的语句就可以在便利的基础上完成线索化，并且，这种线索化的过程对原本的二叉树没有造成任何影响，二叉树还是原来的那个二叉树，从没有发生丝丝改变 ^ _ ^

  但是有一点区别就是节点的数据结构的问题，链表中需要保存下一个节点的指针，与二叉树的节点需要组合成一个新的链表的节点，进行链表节点的操作。

  在本历程中使用这样的结构定义。

/**
 *  链表的节点结构定义
 **/
typedef struct __tag_BiTNode_Thread
{
    LinkListNode Header;
    BiTNode *root;
} TBiTNodeThread;

  那么，使用链表进行线索化的代码就可以这样进行编写了。

/**
 *  功 能：
 *      线索化二叉树 -- 利用顺序表
 *  参 数：
 *      root：要线索化的树的根节点
 *      list：顺序表的操作句柄
 *  返回值：
 *      无
 **/
void thread_linklist(BiTNode *root, linkList *list)
{
    if ((root != NULL) && (list != NULL))
    {
        TBiTNodeThread *tmp = malloc(sizeof(TBiTNodeThread));
        /* 将节点的地址赋值给临时节点 */
        tmp->root = root;

        flinklist.insert(list, (LinkListNode *)tmp, flinklist.length(list));
        thread_linklist(root->lchild, list);
        thread_linklist(root->rchild, list);
    }
}

3.3.2、遍历线索化代码实现

  使用链表线索化后的线索二叉树的遍历，其实就是链表的遍历了，那么实现的代码可以这样编写了。

/**
 *  功 能：
 *      遍历利用顺序表线索化二叉树
 *  参 数：
 *      list：顺序表的操作句柄
 *  返回值：
 *      无
 **/
void thread_linklist_print(linkList *list)
{
    int i;
    for (i = 0; i < flinklist.length(list); i++)
    {
        TBiTNodeThread *tmp = (TBiTNodeThread *)flinklist.getNode(list, i);

        printf("%c ", tmp->root->data);
    }

    printf("\n");
}

  这种遍历方式，保留二叉树的结构与关系。需要遍历的时候直接访问链表，快速，方便，简单。

  这个方法线索化后的二叉树在插入节点或者删除节点的是操作就是链表的插入和删除，比较方便。

  但是使用链表进行线索化后，只能确定节点的后继节点，前驱节点依旧难以确定（单链表）。

  此种线索化方式下的中序、后序等可以自行实现，此处不再赘述。

3.4、代码效果测试

  下面为工程文件的结构，使用cmake进行工程管理与编译。

biTree-prev-threaded/
├── CMakeLists.txt
├── README.md
├── image
│   └── image.jpg
├── main
│   └── main.c
├── runtime
└── src
    ├── biTree
    │   ├── biTree.c
    │   └── biTree.h
    ├── linklist
    │   ├── linklist.c
    │   └── linklist.h
    ├── seqlist
    │   ├── seqlist.c
    │   └── seqlist.h
    └── thread
        ├── thread.c
        └── thread.h

8 directories, 12 files

  下面为线索化的操作函数的结构体，方便在主程序中调用并方便修改等等。

typedef struct __func_thread
{
    void (*bylchild)(BiTNode *, BiTNode **);
    void (*bySeqlist)(BiTNode *, seqList *);
    void (*bylinkList)(BiTNode *, linkList *);
    void (*lchild_print)(BiTNode *);
    void (*seqlist_print)(seqList *);
    void (*linklist_print)(linkList *);
} funThread;

extern funThread fthread;

  下面是测试底层功能函数的测试demo，详细代码如下。

#include "../src/thread/thread.h"
#include 
#include 
#include 

/* 在运行测试案例的时候输入的#法创建的二叉树的字符串 */
// ABDH#K###E##CFI###G#J##

int main(int argc, const char *argv[])
{
    int ret = 0;
    BiTNode *tree = NULL;

    // 创建一个二叉树
    printf("请按照先序输入二叉树(空节点用#表示)：");
    tree = fBiTree.create();

    if (tree != NULL)
    {
        printf("二叉树创建成功！\n");
    }
    else
    {
        printf("二叉树创建出现异常！\n");
        ret = -1;
        goto ERROR_END;
    }

    printf("遍历结果列表为：\n");
    printf("     先序遍历输出     |      中序遍历输出     |      后序遍历输出     |    层序遍历输出\n");
    fBiTree.prevOrder(tree);
    printf("| ");
    fBiTree.inOrder(tree);
    printf("| ");
    fBiTree.postOrder(tree);
    printf("| ");
    fBiTree.levelOrder(tree);
    printf("\n\n");

    int leaf = 0;
    fBiTree.leafNum(tree, &leaf);
    printf("节点的个数 = %d  叶子节点的个数 = %d, 树的深度/高度 = %d\n", fBiTree.nodeNum(tree), leaf, fBiTree.depth(tree));

    BiTNode *copyTree1 = fBiTree.copy(tree);
    BiTNode *copyTree2 = fBiTree.copy(tree);

    /**
     *  线索化二叉树
     *  线索化二叉树会修改二叉树的结构，修改后将不再是原本的二叉树的结构了
     **/
    BiTNode *p = NULL;
    fthread.bylchild(copyTree1, &p);

    printf("copy树的左孩子前序线索化遍历输出：");
    fthread.lchild_print(copyTree1);
    printf("\n");

    /* 创建一个顺序表 */
    seqList *seqlist = fSeqList.create(fBiTree.nodeNum(tree));
    printf("copy树的顺序表前序线索化遍历输出：");
    fthread.bySeqlist(copyTree2, seqlist);
    fthread.seqlist_print(seqlist);

    printf("copy树的顺序表前序线索化后遍历结果列表为：\n");
    printf("     先序遍历输出     |      中序遍历输出     |      后序遍历输出     |    层序遍历输出\n");
    fBiTree.prevOrder(copyTree2);
    printf("| ");
    fBiTree.inOrder(copyTree2);
    printf("| ");
    fBiTree.postOrder(copyTree2);
    printf("| ");
    fBiTree.levelOrder(copyTree2);
    printf("\n\n");

    /* 创建一个链式表 */
    linkList *linklist = flinklist.create();
    printf("copy树的链式表前序线索化遍历输出：");
    fthread.bylinkList(copyTree2, linklist);
    fthread.linklist_print(linklist);
    printf("\n");

    printf("copy树的链式表前序线索化后遍历结果列表为：\n");
    printf("     先序遍历输出     |      中序遍历输出     |      后序遍历输出     |    层序遍历输出\n");
    fBiTree.prevOrder(copyTree2);
    printf("| ");
    fBiTree.inOrder(copyTree2);
    printf("| ");
    fBiTree.postOrder(copyTree2);
    printf("| ");
    fBiTree.levelOrder(copyTree2);
    printf("\n\n");

ERROR_END:
    // 释放二叉树
    fBiTree.release(tree);
    /* copyTree1已经在线索化的过程中被修改，此时按照原先的释放方式释放的话出现异常 */
    // fBiTree.release(copyTree1);
    fBiTree.release(copyTree2);

    // 销毁顺序表
    fSeqList.destory(seqlist);
    // 销毁链表
    flinklist.destory(&linklist);

    printf("system exit with return code %d\n", ret);

    return ret;
}

  编译运行结果图下图所示。

图3.8 编译运行效果图

  
  上面运行时候输入了一个二叉树，那么为了更加清晰的结合代码查看，下面是运行中输入的二叉树的结构。

  

图3.9 程序运行中输入的二叉树的结构

  

四、简单的总结

表4.1 线索化方式的对比表

编号	线索化方式	是否修改原二叉树	前驱	后继	插入删除	节点访问
01	空指针域	是，原二叉树左右子树关系被改变	未 知	lchild指针域	插入节点或者删除节点操作复杂	只能从头开始访问
02	顺 序 表	否，原二叉树左右子树关系保留	下标-1	下标+1	插入删除节点过程复杂，顺序表内存扩展复杂	直接确定下标访问
03	链   表	否，原二叉树左右子树关系保留	未 知	链表next指针域	比较方便，链表的插入和删除操作	只能从头开始访问

  是的，看到这个地方你应该也会有同样的想法了，除了空指针域线索化方式之外，其他的线索化方式都是重新创建了一种数据结构，将一个二叉树的某种遍历的顺序（先序、中序、后序、层序）用另外的一种数据结构形式保存起来了。那根据我们的实际的需求，可以创建任何一种形式的结构去保存树（包括产品经理都想不到的形式 ^ _ ^… ）。

  那么上面的这个表表我们又可以再次扩展一下。。。

  注意：

    下面表格中像模像样记录对比的方法均为博主好奇调皮爱搞事闲的D疼爱总结的，请不要太过于较真。。。。

表4.2 线索化方式的扩展对比表

编号	线索化方式	是否修改原二叉树	前驱	后继	节点访问	优缺点
01	双  向  链  表	否	pre指针域	next指针域	任意访问	占用内存较大
02	双向循环链表	否	pre指针域	next指针域	任意访问	占用内存较大
…	…	…	…	…	…	…

  至于双向链表和双向循环链表线索化的代码就不在编写并且测试，其实就是将上面测试案例中的单链表换成对应的链表形式就可以了。有兴趣的可以自行测试了。。。。

  原本打算将另外的线索化的方法在本文后面继续写完，但是后来发现本文就已经超过 20000 个字了，一来害怕影响阅读者看见这么长的内容直接退出，二来后面要说的线索化方式也比较大众且资料众多，但是都不怎么详细，所以打算好好的仔仔细细的进行分析说明。所以干脆就重新在开个炉灶吧。

  
  好啦，废话不多说，总结写作不易，如果你喜欢这篇文章或者对你有用，请动动你发财的小手手帮忙点个赞，当然关注一波那就更好了，好啦，就到这儿了，么么哒(* ￣3)(ε￣ *)。

上一篇：数据结构（十五） – C语言版 – 树 - 二叉树的操作进阶之创建、插入、删除、查询、销毁
下一篇：数据结构（十七） – C语言版 – 树 - 二叉树的线索化及遍历 – 先序线索化、中序线索化、后序线索化