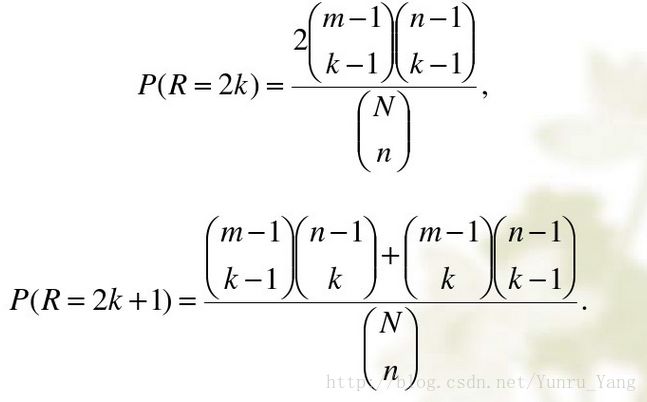【通俗向】非参数检验（一）游程检验（Runs test）

游程检验个人感觉是在日常分析过程中很有用的一个检验。

游程检验主要检验一件事情发生的概率是否为随机的。

游程检验的原理其实很简单：引入一个参数看看整个数列的分布，还是从最简单的抛硬币开始。

比如抛硬币，正面是1，反面是0。

抛两次，出现一次1，出现一次0。计这个数列为（1，0）

游程就是连续1的个数和连续0的个数，在这里游程就是两个；但是正反面只抛两次判定随机是没有意义的。

那么我们再做点实验，比如抛了10次，出现硬币的排列情况有下述三种，
1. （1,0,1,0,1,0,1,0,1,0）
2. （1,1,1,1,1,0,0,0,0,0）
3. （1,0,0,1,1,1,1,0,0,0）

分别看看游程的数量和对应的概率：
1. 连续的1的数量是5,连续的0的数量也是5（实际上没有连续的1和0），所以游程是10，假设这个数列是随机的话，计算下随机的概率：

首先，概率是出现这种情况的次数/所有试验次数，所有试验次数就是任意抛10次硬币，出现5个1,5个0的概率，也就是C10(5) 其中10是下标，5是上标，也就是10个中抽5个的次数。

分子上就是出现这个1,0周期性排列的概率，看到有5个0,5个1在交错排列，可以认为在5个0中插入一个楔子A，在5个1中插入一个楔子B，把这个数列分开；而这四个楔子恰好能把数列分开成五个一的概率就是1，同理分开1之后，只能是0，然后这个随机概率和1,0互换的概率是一致的，所以有两种情况是随机的，那么分子就是2，其实分子就是：

在楔子的数量中，全为1的概率，在另一个楔子的数量中，抽取全是0的概率，然后加一起；

公式就是

后续的几个同理；

下面用R进行测算

library(lawstat)
par(mfrow=c(1,3))
y1<-rep(c(1,0),5)
y2<-c(rep(1,5),rep(0,5))
y3<-c(1,0,0,1,1,1,1,0,0,0)
runs.test(y1,plot.it=T)
runs.test(y2,plot.it=T)
runs.test(y3,plot.it=T)

可以看到，结果

> runs.test(y1,plot.it=T)

    Runs Test - Two sided

data:  y1
Standardized Runs Statistic = 2.6833, p-value = 0.00729

> runs.test(y2,plot.it=T)

    Runs Test - Two sided

data:  y2
Standardized Runs Statistic = -2.6833, p-value = 0.00729

> runs.test(y3,plot.it=T)

    Runs Test - Two sided

data:  y3
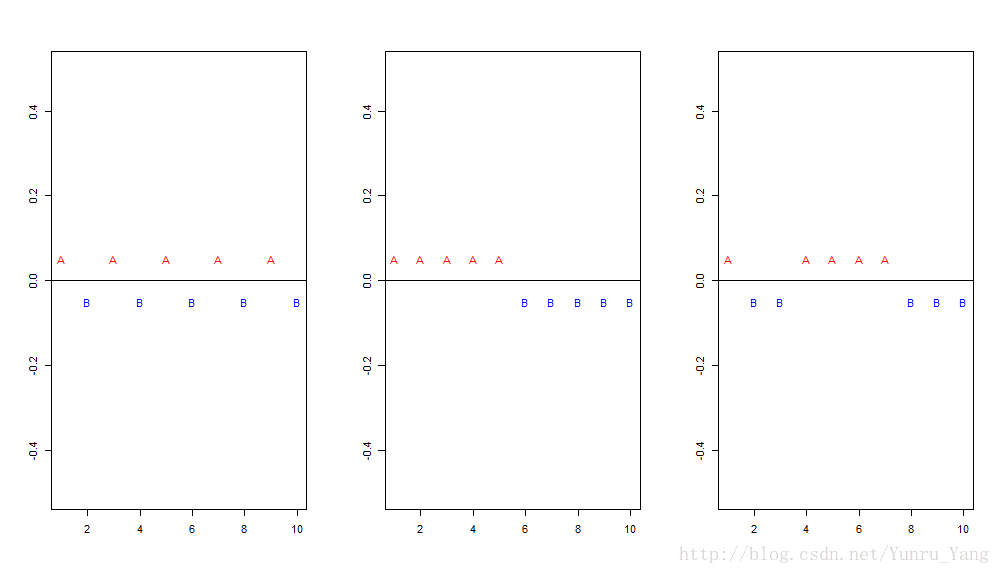
Standardized Runs Statistic = -1.3416, p-value = 0.1797

也就是说1,2的p值不到0.01，可以拒绝是随机的假设，而3无法拒绝是随机的假设；

其实从图上也能看出，1在围绕0振动，2呈现周期性趋势，而3暂无良好的趋势解释