二叉树编程题总结

• 求二叉树的最远两个结点的距离
• 由前序遍历和中序遍历重建二叉树
• 判断一棵树是否是完全二叉树
• 求二叉树两个节点的最近公共祖先
• 将二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点，只能调整树中结点指针的指向

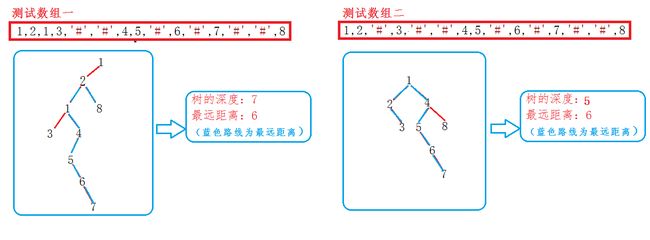
求二叉树的最远两个结点的距离

短短的代码中其实涉及到了三道题目：

• 利用已知序列递归的建一棵二叉树
• 递归的求一棵树的深度
• 求二叉树中距离最远的两个节点的距离
• 利用类似的思想判断一棵树是否为平衡二叉树；

利用递归求树的深度的思想，在其中加入一个最大距离的引用的参数，利用了引用参数的特性，即可求得最大距离，比较简单，下面列出代码及图示；

给出两组测试用例的图示：

#include 
using namespace std;

struct Node {
    int _data;
    Node* _left;
    Node* _right;
    Node(const int & data): _data(data), _left(NULL), _right(NULL){}
};
class BinaryTree {
    Node* _root;
public:
    BinaryTree(int * arr, size_t size) {
        int index = 0;
        _root = _GreatTree(arr, size, '#', index);
    }
    // 前序递归建树
    Node* _GreatTree(int* arr, size_t size, int invalid, int & index) {
        Node* root = NULL;
        if (index < size && arr[index] != invalid) {
            root = new Node(arr[index]);
            root->_left = _GreatTree(arr, size, invalid, ++index);
            root->_right = _GreatTree(arr, size, invalid, ++index);
        }
        return root;
    }
    // 求二叉树最远两个节点的距离
    void MaxDistance() {
        //利用递归不断的往回带
        int maxLength = 0;   // 最远距离
        cout << _maxDistance(_root, maxLength) << endl;  // 顺带求了一下树的深度
        cout << maxLength << endl;       // 最后比较到根节点，输出最远距离
    }
    // 扩展，我们在判断一棵树是否是平衡二叉树的时候同样是利用这种思想
    bool isBalance() {
        int height = 0;
        return _isBalance(_root, height);
    }
protected:   // 保护实现细节
    // 后序遍历的方式，边遍历边判断
    bool _isBalance(Node* root, int & height) {
        if (root == NULL)
            return true;

        int leftHeight = height;
        if (_isBalance(root->_left, leftHeight) == false)
            return false;
        int rightHeight = height;
        if (_isBalance(root->_right, rightHeight) == false)
            return false;
        height = leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
        return abs(rightHeight - leftHeight) < 2;
    }
    int _maxDistance(Node* root, int & maxLength) {
        if (root == NULL)
            return 0;    // 表示到了叶子节点
        int leftDepth = _maxDistance(root->_left, maxLength);     // 左子树深度
        int rightDepth = _maxDistance(root->_right, maxLength);   // 右子树深度
        int tmp = leftDepth + rightDepth;
        if (tmp > maxLength)
            maxLength = tmp;
        // 当前节点的深度是左右子树最大的深度基础上+1
        return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
    }

};
int main() {
    // 根据给出的序列建一颗二叉树，其中'#'代表非法值。即用来表示NULL；
    // 给出两组测试数据
    int array[15] = {1, 2, '#', 3, '#', '#', 4, 5, '#', 6, '#', 7, '#', '#', 8};
    // int array[15] = {1,2,1,3,'#','#',4,5,'#',6,'#',7,'#','#',8};
    BinaryTree b(array, 15);
    b.MaxDistance();
    return 0;
}

由前序遍历和中序遍历重建二叉树

分析：这是一道考察基础的题目，即对二叉树的遍历方式是否有深刻的了解，同时也考察对二叉树的构建的了解，通常给定一个序列构建二叉树的方式是利用前序遍历并且结合非法值的方式进行构建，这个在第一题的实现中已经有了体现；

目前我们所了解的二叉树的遍历方式有四种：前，中，后，层序遍历；
其中前序遍历是深度优先遍历，层序遍历是广度优先遍历（这个会在第三题中用到）；当然，这个属于只是扩展；

本题所考察的前序和中序遍历构建二叉树，我们以下面这两个序列为例，分析：
（前序序列：1 2 3 4 5 6 - 中序序列:3 2 4 1 6 5）

我们根据前序和中序的特性，划分出了根节点的左子树和右子树，那么此时，我们至少知道了这棵树的根节点，也就是拥有了根节点，还知道了左右子树的节点个数，接下来，就该去创建它的左子树和右子树，而左右子树又可以单独的看作是一棵树，我们可以知道左右子树的根节点，怎么知道的？
前序遍历就在那放着，根结点1 的右边第一个不就是左子树的根节点，而根据中序遍历我们又知道左子树的节点个数，1 往右 3 个结点之后不就是5；那么 5 就是 1 的右子树的根节点，以此类推，这棵树都所有结点我们都拥有了，树不就建出来了，下面给出一个图示：

Node* _GreatTree(int* prestart, int* preend, int* instart, int *inend) {
        Node* root = new Node(*prestart);

        // 如果当前只有一个节点，则将创建好的这个节点返回
        if (prestart == preend && instart == inend)
            return root;

        // 找到中序遍历中的根节点
        int * rootInorder = instart;
        while (rootInorder <= inend && *prestart != * rootInorder)
            ++rootInorder;

        // 创建左子树
        int length = rootInorder - instart; // 左子树的节点数量
        int *leftpreend = prestart + length;
        // 如果当前根节点有左子树，创建左子树
        if (length > 0)
            root->_left = _GreatTree(prestart+1, leftpreend, instart, instart+length);

        // //如果当前根节点有右子树，则创建右子树
        int * rightprestart = leftpreend + 1;  // 右子树前序遍历的开始
        if (length < preend - prestart)
            root->_right = _GreatTree(rightprestart, preend, rootInorder+1, inend);
        return root;

    }

Node* build(int s1, int e1, int s2, int e2) {
    Node* ret = new Node(str1[s1]);   // 该节点字符为前序遍历中的第一个字符
    int rootIdx;
    for (int i = s2; i <= e2; i++) {   // 查找该根节点字符在中序遍历中的位置
        if (str2[i] == str1[s1]) {
            rootIdx = i;
            break;
        }
    }
    int length = rootIdx - s2;
    if (rootIdx != s2) {   // 若左子树不为空
        ret->left = build(s1+1, s1+length, s2, rootIdx-1);
    }
    if (rootIdx != e2) {   // 若右子树不为空
        ret->right = build(s1+length+1, e1, rootIdx+1, e2);
    }
    return ret;
}

判断一棵树是否是完全二叉树

完全二叉树(Complete Binary Tree)
若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。
完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。
一棵二叉树至多只有最下面的一层上的结点的度数可以小于2，并且最下层上的结点都集中在该层最左边的若干位置上，则此二叉树成为完全二叉树。

下面给出这道题基于层序遍历的两种解法：

1）设置标志法

从根节点开始，入队列，如果队列不为空，循环。
遇到第一个没有左儿子或者右儿子的节点，设置标志位，如果之后再遇到有左/右儿子的节点，那么这不是一颗完全二叉树。
图示：

struct Node {
    int _data;
    Node* _left;
    Node* _right;
    Node(const int & data): _data(data), _left(NULL), _right(NULL){}
};
bool isCompleteTree(Node * root) {
    queue<Node* > q;
    q.push(root);
    Node* cur = q.front();
    int flag = 0; // 标志
    while (cur) {
        // 没有左孩子却有右孩子，一定不是完全二叉树
        if (cur->_left == NULL && cur->_right != NULL)
            return false;
        // 如果flag == 1, 并且当前节点有孩子，则false
        if (flag == 1 && (cur->_left != NULL || cur->_right != NULL) )
            return false;
        // 当前节点没有左孩子或者右孩子
        if (cur->_left == NULL || cur->_right == NULL)
            flag = 1;
        if (cur->_left != NULL)
            q.push(cur->_left);
        if (cur->_right != NULL)
            q.push(cur->_right);

        q.pop();
        if (!q.empty())
            cur = q.front();
        else
            cur = NULL;
    }
    return true;
}

2）剩余队列判空法

这个方法同样需要入队列，不同的在于判断的方式，试想一颗完全二叉树，我们把它的所有节点，包括叶子节点的左右空孩子都入队列，通过层序遍历，不断的入队列和出队列的方式，如果遇到第一个队头元素为空，那么如果是完全二叉树的 话，此时一定遍历完了所有节点，队列中剩余的元素肯定全是NULL的节点，也就是叶子节点的空孩子，如若不是如此，那么，这就不是一颗完全二叉树。

图示：

图中省略入队出队过程。

bool isCompleteTree(Node * root) {
    if (root == NULL)
        return false;
    queue q;
    q.push(root);
    Node* cur = q.front();
    // 先将所有的节点以及它们的左右节点入队列
    while (cur) { // 如果遇到第一个空节点停止
        q.push(cur->_left);
        q.push(cur->_right);
        q.pop();
        cur = q.front();
    }
    // 此时应该是完全二叉树的结尾，正确的情况应该是队列中所有元素都是NULL，否则为不是完全二叉树
    while (!q.empty()) {
        if (q.front() != NULL)
            return false;
        q.pop();
    }
    return true;
}

求二叉树两个节点的最近公共祖先

分析： 这道题是剑指offer上的一道题，难点在于全面的考虑各种情况，利用合适的方法解决各种情况；

什么是最近公共祖先？
即从根节点分别到两个节点的路经中最后一个公共节点，即最近公共祖先；

如下图所示：

然后，我们需要分析出都有哪些情况？

1）二叉搜索树
2）带有父指针的二叉树（就是三叉链）
3）一颗普通的树

情况1：

最简单的情景，即本身就是一颗二叉搜索树，即是有关联的，那么我们只要找到一个比其中一个节点大或者等于，并且比另一个节点小或者等于的节点就可以了，这个节点就是最低公共祖先，这个很好理解，就不多做赘述，直接上代码了。

int minCommonAncestor(int x, int y) {
        Node* cur = _root;
        Node* tmp = NULL;
        while (cur) {
            // 比两个目标节点的值都打，继续往左子树找
            if (cur->_data > x && cur->_data > y) {
                tmp = cur;
                cur = cur->_left;
            } else if (cur->_data < x && cur->_data < y) {
                tmp = cur;
                cur = cur->_right;
            }
            // 符合条件找到目标点
            else if ( (cur->_data >= x && cur->_data <= y) || (cur->_data <= x && cur->_data >= y) ) {
                return cur->_data;
            }
        }
    }

情景2：
不是二叉搜索树，但是有父指针的二叉树。

既然有父指针，即是三叉链，那么问题就又变的简单了，熟悉的同学应该很快就发现，这样的话就把问题转化为求两条相交链表的第一个公共节点的问题了，当然，为什么是第一个公共节点？前面说最低公共祖先的概念的时候不是说是从根节点分别到两个节点的最后一个公共节点吗？

不要急，你想想，现在我们有了父节点的话，完全可以从两个目标节点往上遍历，这不就是反着的了，求两个相交节点的 第一个公共节点，出发点不一样；

而从两个目标节点向上遍历的时候又有好几种办法，比如说利用栈，利用长度差的方法，栈的方法我们先不用，留到下一种情景用，这里我们用的 是长度差的方法，何为长度差的方法？

长度差：即我们寻找两个目标节点的时候，顺便把从根节点到他们所经过的路径长度保存起来，分别是count1和count2; 然后求得他们的差值，即长的那条路径比短的那条路径多的节点数，为什么要这样呢？

因为我们需要逆向找路径上的第一个公共节点，而如果从两个目标节点同时出发的话，肯定就不是我么想要的结果了，看着上面那个图所举得例子，如果7和6同时开始遍历，那就有问题了，而如果我们让路径长的那个节点先走上他们的长度差的节点后，两个节点再同时向上遍历，第一个相同的节点不就是第一个公共节点了（当然，我们排除出现相同节点的可能性）；

//3. 判断一棵树是否是完全二叉树
#include
#include

using namespace std;

struct Node{
    int _data;
    Node* _left;
    Node* _right;
    Node* _parent;

    Node(const int& data):_data(data),_left(NULL),_right(NULL),_parent(NULL){}
};
class BinaryTree {
    Node* _root;
public:
    BinaryTree(int* arr, int size) {
        int index = 0;
        Node* parent = NULL;
        _root = _GreatTree(arr, size, '#', index, parent);
    }

    //前序递归建树
    Node* _GreatTree(int* arr, int size,int invalid, int& index,Node* parent) {
        Node* root = NULL;
        if(index < size && arr[index] != invalid) {
            root = new Node(arr[index]);
            root->_parent = parent;
            root->_left = _GreatTree(arr,size,invalid,++index,root);
            root->_right = _GreatTree(arr,size,invalid,++index,root);
        }
        return root;
    }

    //查找最小公共祖先
    int MinCommonAncestor(int x,int y) {
        // 根据已知节点向上查找到根节点，求两个链表的第一个交点
        // 前提都是建立在没有重复元素的二叉树中

        if(x == y)
            return x;

        //不考虑返回空的情况，即暂时不考虑非法输入
        Node* nodeone = NULL;
        _FindNode(_root, x, nodeone);
        Node* nodetwo = NULL;
        _FindNode(_root, y, nodetwo);

        //采用找两个链表第一个公共节点的方法求解，三种方法，穷举，辅助栈，和求长度差；
        //利用第三种方法

        int count1 = 1;
        int count2 = 1;
        Node* tmp = nodeone;

        while(tmp->_parent) {
            ++count1;
            tmp = tmp->_parent;
        }
        tmp = nodetwo;

        while(tmp->_parent) {
            ++count2;
            tmp = tmp->_parent;
        }

        //求出长度差
        int len = abs(count1 - count2);
        if (count1 >= count2)
            return _FindFirstNode(nodeone, nodetwo, len);
        else
            return _FindFirstNode(nodetwo, nodeone, len);
    }
protected:
    int _FindFirstNode(Node* one, Node* two, int len) {
        while(len--)
            one = one->_parent;

        while(one != two) {
            one = one->_parent;
            two = two->_parent;
        }
        return one->_data;
    }

    //寻找节点
    void  _FindNode(Node* root, const int data, Node*& node) {
        //前序遍历，深度优先遍历
        if(root == NULL)
            return;

        if(root->_data == data)
            node = root;

         _FindNode(root->_left, data, node);
         _FindNode(root->_right, data, node);
    }
};

将二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点，只能调整树中结点指针的指向

二叉搜索树，也是有分别指向左子树和右子树的指针，而且中序遍历有序；
而把二叉搜索树变为有序的双向链表，第一点不免想到的肯定是中序遍历的 方法，然后就是改变指针的指向，因为不允许创建新的节点，而改变指针的指向的话，就简单很多了，只要让left变为指向前一个节点的指针，right变为指向后一个节点的 指针就可以了，当然，代码的实现过程中肯定会有些许的细节差异。

Node* TurnToList() {
    Node* prev = NULL;
    _TurnToList(_root, prev);
    // 返回双向链表的头结点
    Node* cur = _root;
    while (cur && cur->_left)
        cur = cur->_left;
    return cur;
}
void _TurnToList(Node* root, Node*& prev) {
    if (root == NULL)
        return;
    _TurnToList(root->_left, prev);
    if (prev != NULL)
        prev->_right = root;
    prev = root;
    _TurnToList(root->_right,prev);
}