pca和svd的区别与联系【musk数据集】以及如何使用pca和svd降维及其可视化，最后附上使用logistic回归的结果
数据和代码链接附上：https://github.com/ciecus/homeworks/tree/master/pca_svd
欢迎fork我一起学习一起进步呀
1.1 数据集—musk
Musk数据集UCI机器学习实验室于1949年9月建立的数据集，我们采用了版本一的数据集。该数据集共有476条数据，每条数据有168个属性，没有缺失值，适合二元分类任务。
数据集中包含了92个分子，其中47个被认定为musk，剩下45个被认定为non-musk，166个特征描述了这些分子的形状，构象，因为分子键可以旋转，所以一个分子可能有很多不同的形状，为了生成这个数据集，我们生成了分子的低能构象，并且过滤了高度相似的构象，保留了476个构象，musk分子构象如图1所示。
图1 musk分子构象
数据集的属性描述表1所示：
表1：musk数据集属性描述
| 列数 |
属性名 |
内容 |
| 1 |
molecule_name |
每个分子的符号名称。MUSK-188, NON-MUSK-jp13 |
| 2 |
conformation_name |
每个构象的符号名称。MOL_ISO+CONF |
| 3-165 |
"distance features" along rays |
光线的“距离特征”, 相对于沿每条光线放置的原点进行测量的。任何对数据的实验都应该将这些特征值视为处于任意连续尺度上。 |
| 166 |
OXY-DIS |
分子中氧原子到3-space中指定点的距离。 |
| 167-168 |
displacement from the designated point |
从指定点位移 |
| 169 |
Class |
0：non-musk，1：musk |
1.2分析方法—pca+SVD
1.2.1 pca介绍
主成分分析（principal component analysis）是一种常见的数据降维方法，其目的是在“信息”损失较小的前提下，将高维的数据转换到低维，从而减小计算量。
降维的必要性在于可以解决以下几个问题：1.多重共线性--预测变量之间相互关联。多重共线性会导致解空间的不稳定，从而可能导致结果的不连贯。2.高维空间本身具有稀疏性。一维正态分布有68%的值落于正负标准差之间，而在十维空间上只有0.02%。3.过多的变量会妨碍查找规律的建立。4.仅在变量层面上分析可能会忽略变量之间的潜在联系。例如几个预测变量可能落入仅反映数据某一方面特征的一个组内。
PCA的本质就是找一些投影方向，使得数据在这些投影方向上的方差最大，而且这些投影方向是相互正交的。
具体实践步骤可以分为5步：
（1）特征中心化
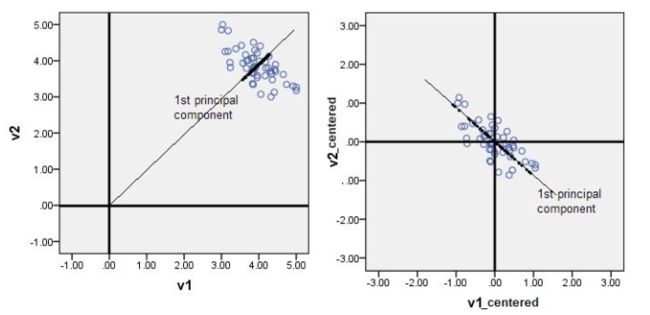
在PCA中，中心化后的数据有助于后续在求协方差的步骤中减少计算量，同时中心化后的数据才能比较好地“概括”原来的数据（如图2）
图2 特征中心化作用
（2）求特征的协方差矩阵/相关系数矩阵
特征之间度量单位不同，或者度量单位相同但是数值上差异很大，这个时候用协方差矩阵的特征值衡量贡献率就容易受到方差大的特征的影响，所以这个时候用相关系数计算比较合适。相关系数矩阵就相当于特征归一化之后的协方差矩阵。
（3） 计算协方差矩阵、相关系数矩阵的特征值和特征向量，将特征向量和特征值根据特征值的大小从大到小排序
（4） 计算贡献率，选取前k个特征值对应的特征向量组成的特征向量矩阵
（5） 降维后的数据就等于原始数据乘以特征向量矩阵。
def pca(x,d):
meanValue=np.mean(x,0)
x = x-meanValue
cov_mat = np.cov(x,rowvar = 0)
eigVal, eigVec = np.linalg.eig(mat(cov_mat))
#取最大的d个特征值
eigValSorted_indices = np.argsort(eigVal)
eigVec_d = eigVec[:,eigValSorted_indices[:-d-1:-1]] #-d-1前加:才能向左切
eigVal_d = eigVal[eigValSorted_indices[:-d-1:-1]]
contributions = round(float(sum(eigVal_d)/sum(eigVal)),2)
#print("----------------------------eig vectors----------------\n",eigVec_d)
#print("----------------------------eig values----------------\n",eigVal_d)
#print("----------------------------contributions----------------\n",contributions)
return eigVec_d,eigVal_d,contributions1.2.2 svd介绍
奇异值分解(Singular Value Decomposition，以下简称SVD)是在机器学习领域广泛应用的算法，它不光可以用于降维算法中的特征分解，还可以用于推荐系统，以及自然语言处理等领域。是很多机器学习算法的基石。
对于任意m × n的矩阵M都可以被分解为M = UΣV*
，如图3所示，其中U是m × m的单位正交矩阵，Σ是m × n的对角元素上是奇异值的矩阵，V是一个n × n 的单位正交矩阵，Σ对角元素上的值σi被称作奇异值。
图3 奇异值分解效果图
U、Σ
、V的求解方法如下：
（1）左奇异值矩阵U：是MM*的特征向量
（2）右奇异值矩阵V：是M*M
的特征向量
（3）奇异值，V上的对角元素：是M*M
或者MM*
非零特征值的平方根
#svd pca
meanValue=np.mean(data1,0)
data1 = data1-meanValue
u, sigma, v = np.linalg.svd(data1[:, :])
#svd_pca_new_data = np.dot(u[:,:13],np.diag(sigma)[:13,:13])
svd_pca_new_data = np.dot(data1,u[:,:13])
print('-------------------------------------svd pca ---------------------------------')
print(sigma[:13])
print(svd_pca_new_data)1.2.3 pca和svd的关系
用PCA降维，需要找到样本协方差矩阵XTX
的最大的d个特征向量，然后用这最大的d个特征向量张成的矩阵来做低维投影降维。可以看出，在这个过程中需要先求出协方差矩阵XTX
，当样本数多样本特征数也多的时候，这个计算量是很大的。
SVD也可以得到协方差矩阵XTX
最大的d个特征向量张成的矩阵，但是SVD有个好处，有一些SVD的实现算法可以不求先求出协方差矩阵XTX
，也能求出右奇异矩阵V。也就是说，我们的PCA算法可以不用做特征分解，而是做SVD来完成。这个方法在样本量很大的时候很有效。实际上，scikit-learn的PCA算法的背后真正的实现就是用的SVD，而不是我们我们认为的暴力特征分解。
假设我们的样本是m×n的矩阵X，如果我们通过SVD找到了矩阵XTX
最大的d个特征向量张成的m×d维矩阵U，则我们如果进行如下处理：
xd×n'=Ud×mTXm×n
可以得到一个d×n的矩阵X’,这个矩阵和我们原来的m×n维样本矩阵X相比，行数从m减到了d，可见对行数进行了压缩。也就是说，左奇异矩阵可以用于行数的压缩。相对的，右奇异矩阵可以用于列数即特征维度的压缩，也就是我们的PCA降维。
1.3 实验
1.3.1 三种pca方法比较
pca的实现我们使用了三种方法：一、对协方差矩阵特征值分解，获取特征值最大的特征向量二、使用svd获得特征向量 三、使用sklearn中的pca方法
from sklearn.decomposition import PCA
meanValue=np.mean(data1,0)
data1 = data1-meanValue
pca_sklearn=PCA(n_components=3).fit(data1)
reducedx = pca_sklearn.fit_transform(data1)
print('-------------------------------------skleran pca ---------------------------------')
print("explained_variance_ratio:",pca_sklearn.explained_variance_ratio_)
print("singular_values",pca_sklearn.singular_values_)
print(reducedx)- 主成分个数的选择
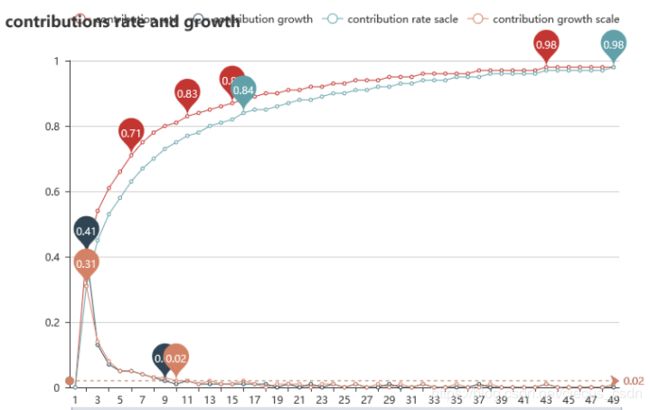
我们使用自己写的pca方法对主成分的贡献率以及贡献增长率进行了分析，如图4所示，其中红色和黑色的线是使用协方差矩阵进行分析的结果，红色为总贡献率，黑线为贡献增长率。橘色和蓝色的线是使用相关系数矩阵进行分析的结果，蓝线为总贡献率，橘线为贡献增长率。我们可以发现（1）使用协方差矩阵和相关系数矩阵的差异主要体现在贡献率上，（2）在13个主成分之后增长率几乎为0。此时无论是使用协方差还是相关系数的贡献率都大于等于80%，所以我们选定用13个主成分进行后面的比较和实验。
def pca_contribution_plt(data,max_dim):
contributions_list = []
for n in range(max_dim):
#print("the eigenvalue number is %d\n"%n)
eigVec_d,eigVal_d,contributions = pca(data,n)
contributions_list.append(contributions)
contribution_growth = [round(contributions_list[i]-contributions_list[i-1],2) for i in range(1,max_dim)]
plt.figure()
plt.plot(range(max_dim),contributions_list)
plt.plot(range(1,max_dim),contribution_growth)
plt.show()
return contributions_list,contribution_growth
def plot(data,max_dim):
contributions_list,contribution_growth = pca_contribution_plt(data,max_dim)
data_scale = preprocessing.scale(data)
contributions_list_scale,contribution_growth_scale = pca_contribution_plt(data_scale,max_dim)
return contributions_list,contribution_growth,contributions_list_scale,contribution_growth_scale
图4 主成分的贡献率和贡献增长率
- 方法比较
特征值比较：
| 分解协方差的特征值 |
分解相关系数的特征值 |
Svd的奇异值 |
Sklearn的奇异值 |
| 453240 144754 77810.6 62335.7 49078.1 46721.8 30678.2 23608.9 18173.2 17244.4 14178.5 12883.3 12292.7 |
51.8813 23.159 12.6725 8.55541 8.18384 6.78398 5.40026 5.0614 3.31324 2.85645 2.57682 2.38175 2.21213 |
14672.7 8292.05 6079.48 5441.46 4828.26 4710.93 3817.35 3348.77 2938.08 2862.01 2595.15 2473.77 2416.41 |
14672.7 8292.05 6079.48 5441.46 4828.26 4710.93 3817.35 3348.77 2938.08 2862.01 2595.15 2473.77 2416.41 |
主成分比较（只比较第一个实例）
| 分解协方差的主成分 |
分解相关系数的主成分 |
Svd的主成分 |
Sklearn的主成分 |
| -118.66637432 -750.09743105 -214.33802756 -643.55969459 169.49700686 54.1440832 96.74821257 -202.7629537 -42.09157408 154.61193861 -77.11861495 25.41700138 2.28442149 |
-0.78784999 8.66447962 -2.43317735 8.10925564 0.14098592 2.40527447 3.27031211 2.0719793 1.29801728 0.19001479 -0.91969795 0.19108686 0.44034676 |
-118.66637432 750.09743105 214.33802756 643.55969459 -169.49700686 54.1440832 96.74821257 -202.7629537 -42.09157408 -154.61193861 77.11861495 -25.41700138 2.28442149 |
118.66637432 750.09743105 214.33802756 -643.55969459 169.49700686 54.1440832 -96.74821257 -202.7629537 -42.09157408 154.61193861 -77.11861495 25.41700138 -2.28442149 |
可以发现虽然特征值不同，但是最原始矩阵的作用效果相同，提取的主成分也相同。
1.4 降维数据可视化
#visualize 2d
def visualize_plot_2D(reduced_x,y):
red_x,red_y=[],[]
blue_x,blue_y=[],[]
for i in range(len(reduced_x)):
if y[i] ==0:
red_x.append(reduced_x[i][0])
red_y.append(reduced_x[i][1])
else:
blue_x.append(reduced_x[i][0])
blue_y.append(reduced_x[i][1])
plt.scatter(red_x,red_y,c='r',marker='x')
plt.scatter(blue_x,blue_y,c='b',marker='D')
plt.title('pca visualize 2d')
plt.show()
visualize_plot_2D(svd_pca_new_data,target1)
#visualize 3d
def visualize_plot_3D(reduced_x,y):
red_x,red_y,red_z=[],[],[]
blue_x,blue_y,blue_z=[],[],[]
for i in range(len(reduced_x)):
if y[i] ==0:
red_x.append(reduced_x[i][0])
red_y.append(reduced_x[i][1])
red_z.append(reduced_x[i][2])
else:
blue_x.append(reduced_x[i][0])
blue_y.append(reduced_x[i][1])
blue_z.append(reduced_x[i][2])
fig = plt.figure(figsize=(8,8))
ax = fig.add_subplot(111, projection='3d')
plt.rcParams['legend.fontsize'] = 10
ax.plot(red_x,red_y,red_z, 'o', markersize=8, color='blue', alpha=0.5, label='class1')
ax.plot(blue_x,blue_y,blue_z, '^', markersize=8, alpha=0.5, color='red', label='class2')
plt.title('pca visualize 3d')
ax.legend(loc='upper right')
plt.show()
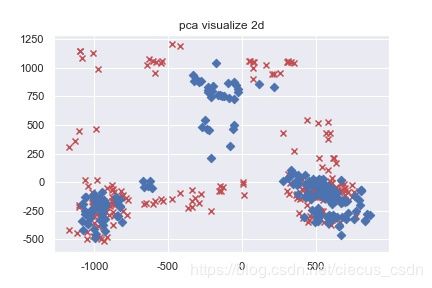
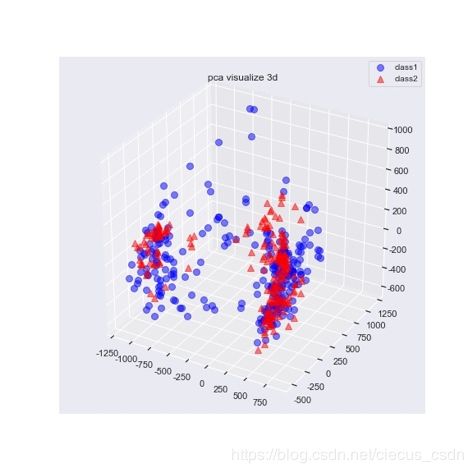
visualize_plot_3D(svd_pca_new_data,target1)图5 降维之后的二维和三维可视化效果
由之前实验可知，两个主成分和三个主成分包含了不到50%的信息，所以不能很好的分类。
1.5 降维数据分类分析
使用logistic regression对降维后的数据进行分类预测，采用5折交叉验证，评估指标为精准度，召回率和准确率。
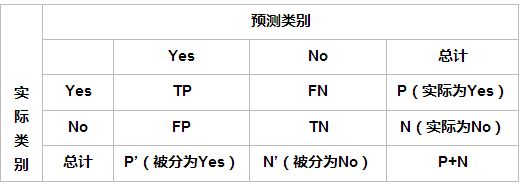
PRECISION= TPTP+FP
RECALL= TPTP+FN
ACCURACY= TP+TNTP+TN+FP+FN
|
|
|
1 |
2 |
3 |
4 |
5 |
平均 |
| 训练集 |
Precison |
71.13% |
70% |
79.26% |
82.21% |
78.57% |
76.23% |
| Recall |
62.16% |
56.25% |
78.01% |
82.61% |
79.71% |
71.75% |
|
| Accuracy |
81.58% |
80.05% |
78.84% |
80.84% |
77.17% |
79.70% |
|
| 测试集 |
Precision |
100% |
100% |
36.36% |
0 |
0 |
47.27% |
| Recall |
46.88% |
54.74% |
100% |
0 |
0 |
40.32% |
|
| Accuary |
46.88% |
54.74% |
70.53% |
54.74% |
76.84% |
60.75% |
import tensorflow as tf
from sklearn.model_selection import KFold
import pandas as pd
def softmax_function(x_train,y_train,x_test,y_test):
loss_list = []
x = tf.placeholder(tf.float32,shape = (None,13))
y = tf.placeholder(tf.float32,shape = (None,2)) #predict
#用softmax 构建模型
w = tf.Variable(tf.zeros([13,2]))
b = tf.Variable(tf.zeros([2]))
pred = tf.nn.softmax(tf.matmul(x,w)+b)
#损失函数（交叉熵）
with tf.name_scope('loss'):
loss = tf.reduce_mean(-tf.reduce_sum(y*tf.log(pred),1))
tf.summary.scalar('loss',loss)
#梯度下降
optimizer = tf.train.GradientDescentOptimizer(0.05).minimize(loss)
#准确率
accuracy = tf.reduce_mean(tf.cast(tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1)), tf.float32))
#加载session 图
with tf.Session() as sess:
#初始化所有变量
init = tf.global_variables_initializer()
sess.run(init)
#开始训练
for epoch in range(10000):
sess.run(optimizer,feed_dict={x:x_train,y:y_train})
loss_list.append(sess.run(loss,feed_dict={x:x_train,y:y_train}))
print('train accuracy:',sess.run(accuracy,feed_dict={x:x_train,y:y_train}))
print('test accuracy:',sess.run(accuracy,feed_dict={x:x_test,y:y_test}))
plt.figure()
plt.plot(range(10000),loss_list)
X = svd_pca_new_data
Y = y1
KF=KFold(n_splits=5)
i = 1
for train_index,test_index in KF.split(X):
print('for %d fold'%i)
i+=1
X_train,X_test=X[train_index],X[test_index]
Y_train,Y_test=Y[train_index],Y[test_index]
softmax_function(X_train,Y_train,X_test,Y_test)1.6 总结
svd是一种矩阵分解的方法，在pca降维的时候使用svd可以起到更好的效果。