在PCA降维前对数据作标准化操作是重要且必要的

当数据维数很高的时候，我们可以用PCA降维，但是降维前通常我们要对数据进行标准化，为什么要这样做？这有什么好处？

原因有以下三点：

1. 从PCA（主成分分析）背后所对应的数学理论SVD(矩阵的奇异值分解）来说，奇异值分解本身是完全不需要对矩阵中的元素做标准化或者去中心化的。但是对于机器学习，我们通常会对矩阵（也就是数据）的每一列先进行标准化。
2. 有时候我们在特征工程阶段，使用某些特征提取算子（eg:HOG）提取的图像特征维度很高。PCA则用于高维数据的降维，它可以将原来高维的数据投影到某个低维的空间上并使得其方差尽量大。如果数据其中某一特征（矩阵的某一列）的数值特别大，那么它在整个误差计算的比重上就很大，那么可以想象在投影到低维空间之后，为了使低秩分解逼近原数据，整个投影会去努力逼近最大的那一个特征，而忽略数值比较小的特征。因为在建模前我们并不知道每个特征的重要性，这很可能导致了大量的信息缺失。为了“公平”起见，防止过分捕捉某些数值大的特征，我们会对每个特征先进行标准化处理，使得它们的大小都在相同的范围内，然后再进行PCA。

3. 从计算的角度讲，PCA通常是数值近似分解，而非求特征值、奇异值得到解析解，所以当我们使用梯度下降等算法进行PCA的时候，我们最好先要对数据进行标准化，这是有利于梯度下降法的收敛。

   ---

   此时有人可能有疑问了，如果我事先是知道某个维度的重要性呢？

         答：如果已知某维度比较重要，可以乘上对应的系数。然后再是PCA的问题。

我在使用机器学习方法作拉链布带缺陷检测的时候，代码是这样的：

训练阶段：

from sklearn import preprocessing
from sklearn.decomposition import IncrementalPCA
from sklearn.externals import joblib

"对训练数据标准化"
scaler = preprocessing.StandardScaler()
x = scaler.fit_transform(x)             # x为整个训练集的特征
"joblib库函数用来保存和加载模型，dump用来保存，load用来加载"
joblib.dump(scaler, model_path + '/scaler_belt.model')

"使用PCA降到feat_len维"
ipca = IncrementalPCA(n_components=feat_len)  
x = ipca.fit_transform(x)
"保存训练集中的PCA降维参数，直接使用其对象转换测试集数据"
joblib.dump(ipca, model_path + '/pca.model')

测试阶段：

from sklearn.externals import joblib

"数据标准化"
"加载训练集上的标准化模型"
scaler = joblib.load(model_path + "/scaler_belt.model")
"features 是整个测试集的特征"
features = scaler.fit_transform(features)

"对整个测试集特征 PCA 降维"
"加载训练集上的 PCA 模型"
pca = joblib.load(model_path + "/pca.model")
features = pca.transform(features)

 

---

上面是对整个测试集的特征进行PCA降维。但是实际业务场景可能是来一张图像，测试一张图像。那么如何对单张图像的特征作PCA降维呢？

from sklearn.externals import joblib

"加载训练集上的 PCA 模型"
pca = joblib.load(model_path + '/pca.model')  
"这里的feat是特征提取算子在单张图像上提取到的特征"
feat_m = [feat, ]
feat = pca.transform(feat_m)[0]

---

如果PCA前没有作数据标准化：

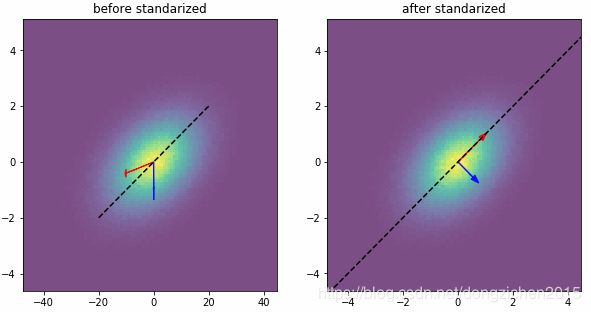
      没做标准化的PCA是找covariance matrix的eigenvector，标准化后的PCA是找correlation matrix的eigenvector。如第一点，如果没有做标准化，eigenvector会偏向方差最大的变量，偏离理论上的最佳值。

      举例说明。假设一个2维Gaussian，correlation matrix是[1 0.4;0.4 1], std(x1)=10,std(x2)=1。理论上最佳的分解向量是椭圆的长轴，如果没有做标准化，PCA算出的向量和长轴会有偏差。标准化后偏差会减到很小。

 

#standarization of PCA
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
np.set_printoptions(precision=3)
np.random.seed(0)
n=1000000
mu=[0,0]
corr=np.array([[1.,.4],[.4,1.]])
std_vector=[10.,1]

A_ori=np.random.multivariate_normal(mu,corr,n)
A_scaled=np.matmul(A_ori,np.diag(std_vector))
scaler = StandardScaler()
scaler.fit(A_scaled)
A_standarized=scaler.transform(A_scaled)

pca = PCA()
pca.fit(A_scaled)
pca1 = PCA()
pca1.fit(A_standarized)

print('Correlation Coefficient matrix is:')
print(corr)
print('std vector is:')
print(std_vector)

print('Covariance matrix is:')
print(np.cov(A_scaled.T))

print('---Before standarization---')
print('Components:')
print(pca.components_)
print('Sigular values:')
print(pca.explained_variance_)

print('---After standarization---')
print('Components:')
print(pca1.components_)
print('Sigular values:')
print(pca1.explained_variance_)

# draw PCA components
t1=np.linspace(-20,20,100)
t2=t1*std_vector[1]/std_vector[0]

plt.figure(figsize=[10,5])
plt.subplot(121)
plt.hist2d(A_scaled[:,0],A_scaled[:,1],100,alpha=0.7)
plt.plot(t1,t2,'--k')
c=pca.components_
r=np.sqrt(pca.explained_variance_)
plt.arrow(0,0,c[0,0]*r[0],c[0,1]*r[0],color='red',head_width=.3)
plt.arrow(0,0,c[1,0]*r[1],c[1,1]*r[1],color='blue',head_width=.3)
# plt.axis('equal')
plt.title('before standarized')

t1=np.linspace(-20,20,100)
cov=np.cov(A_standarized.T)
t2=t1*cov[1,1]
plt.subplot(122)
plt.hist2d(A_standarized[:,0],A_standarized[:,1],100,alpha=0.7)
plt.plot(t1,t2,'--k')
c=pca1.components_
r=np.sqrt(pca1.explained_variance_)
plt.arrow(0,0,c[0,0]*r[0],c[0,1]*r[0],color='red',head_width=.2)
plt.arrow(0,0,c[1,0]*r[1],c[1,1]*r[1],color='blue',head_width=.2)
# plt.axis('equal')
plt.title('after standarized')
plt.show()