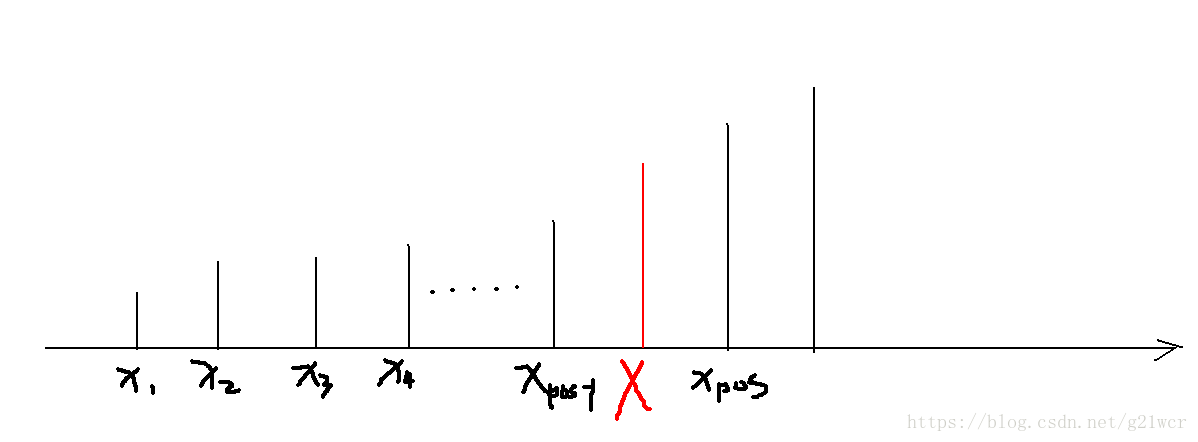【切比雪夫距离转曼哈顿距离】棋盘问题
【题目描述】
小O 对国际象棋有着浓厚的兴趣,因为他水平高超,每次人机对战他总是轻松获胜,所
以他决定自己跟自己下国际象棋。
小O 的棋盘非常大,达到了 10^9*10^9,现在他在棋盘上摆放了 n 个国王,并对你提出
了q次询问,每次询问指定一个坐标,问将所有国王从初始位置全部移动到这个坐标所需要
的最小步数是多少,询问之间相互独立,也就是说每次询问结束后国王会全部回到原来位置。
注意:由于小 O担心大家无法理解过于高深的规则,所以在本题中,国王之间不会发生
相互攻击而且多个国王可以同时处在一个格子中, 国际象棋中国王一步只能移动到与其八
连通的格子中。
【输入格式】
第一行一个正整数 T表示数据组数。
对于每组数据,共有(n+q+1)行:
第一行两个数字 n,q分别表示国王数量和询问数量。
接下来n行,每行两个数字 Kxi,Kyi表示国王所在坐标。
接下来q行,每行两个数字 Txi,Tyi表示目标坐标。
【输出格式】
对于每组数据,输出共有q行,每行一个整数表示对应询问的答案。
【输入样例】
1
1 1
233 666
666 233
【输出样例】
433
【数据范围】
N<=1000000,Q<=1000000,
本题共7个测试点,不采用 subtask评测,但每个测试点分值不同.
数据范围中的 X,Y范围表示Kxi,Kyi,Txi,Tyi的范围,未标注即为没有特殊限制
对于全部数据,满足 N的总和不超过10^6 且Q 的总和不超过10^6,输入文件中所有数
字均为正整数且不超过 10^9.
#1:1pt,满足T=n=q=X=Y=1;
#2:3pts,满足 T=1,1<=X,Y<=5,1<=n<=5,q=1;
#3:16pts,满足 T=1,1<=X,Y<=5,1<=n<=5;
#4:11pts,满足 T=1,1<=X,Y<=1000,1<=n,q<=5000;
#5:21pts,满足所有数据中 N*Q的总和不超过 5*10^7;
#6:22pts,满足 T=1,1<=X,Y<=1000;
#7:26pts,无特殊限制。
关于切比雪夫距离和曼哈顿距离
这道题其实就是求所有点到一个点的切比雪夫距离之和。我们把它转化成曼哈顿距离就行了。
具体见代码:
#include
#define ll long long
using namespace std;
const ll maxn=1e6+233;
inline void read(ll &x){
x=0;char ch=getchar();
while(!isdigit(ch)) ch=getchar();
while(isdigit(ch)) x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
}
ll x[maxn],y[maxn];
ll sumx[maxn],sumy[maxn];
ll n,q,T,X,Y,tx,ty;
ll ans;
int main(){
read(T);
while(T--){
read(n),read(q);
for(ll i=1;i<=n;++i) read(tx),read(ty),x[i]=tx+ty,y[i]=tx-ty;
//转化坐标
sort(x+1,x+1+n),sort(y+1,y+1+n);
//坐标排序
for(ll i=1;i<=n;++i) sumx[i]=sumx[i-1]+x[i],sumy[i]=sumy[i-1]+y[i];
//坐标前缀和
for(ll i=1;i<=q;++i){
ll ans=0;
read(tx),read(ty);
X=tx+ty,Y=tx-ty;
ll pos=lower_bound(x+1,x+n+1,X)-x;
ans+=(pos-1)*X-sumx[pos-1]+sumx[n]-sumx[pos-1]-(n-pos+1)*X;
pos=lower_bound(y+1,y+n+1,Y)-y;
ans+=(pos-1)*Y-sumy[pos-1]+sumy[n]-sumy[pos-1]-(n-pos+1)*Y;
printf("%lld\n",ans/2);
}
}
} 其中横坐标的曼哈顿距离和纵坐标的曼哈顿距离是类似的,也是独立的。下面拿横坐标的举个梨子把。
我们要求的就是Σ|x[i]-X|。x[1]到x[pos-1]是小于X的,绝对值拆开就是X-x[i],后面的就是x[i]-X。Y同理。