浅说数学在算法中的重要性
求 1000 以下的 3 或 5 的倍数之和.
比如求10以下3 或 5 的有以下这些数:
3, 5, 6, 9 求和 3+5+6+9 = 23 .
(原题在:http://projecteuler.net/problem=1)
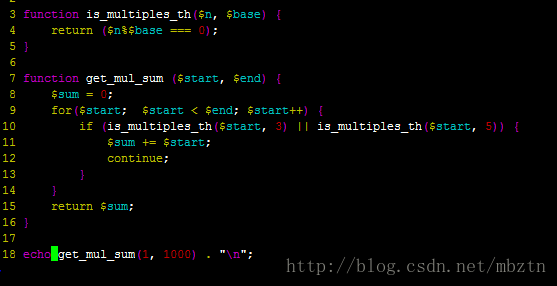
相信很快就可以写出答案, 先用php 代码列出来:
算法解题当然是要追求效率. 分析上面代码求 1000 一下的 3和 5 的倍数之和要循环
999次, 时间复杂度O(n-1).看似还是挺快的..如果 基数达到 100000000000(抛开求和溢出的问题), 你还觉得快吗? 想想有木有其他方法?
当然是有滴.. 直接看 http://projecteuler.net 论坛里面的回复.
nicocarlos
回复:
哦哦.. 看有没有莫名其妙的感觉..
仔细一看是不是有规则..
讨论组中: euler 有回复关于nicocarlos 的解法:( http://projecteuler.net/thread=1 要注册才能看到内容
)
其实题目本身并不难,相对于, 特别是计算机循环(这是人类大脑就处理不来的)计算.相信有很多人都和我一样来用循环得到了结果.
这种循环计算对于人类来说简单遍于理解,当时对于计算机来说太简单太粗暴了(当计算的基数一旦很到就会出问题).
我们使用高中的数学知识来解释一下nicocarlos 的解法.
先回顾一下等差数列相关的计算公式:
通项公式(n是整数):
an = a1 + (n-1)*d
求和:
Sn = (a1 + an)*n /2
在回头看看我们的我难题,先分解问题:
先求 1000 以内 3的倍数的总和有: 3, 6, 9, 12 .. 由求和公式可知道我们缺少 an 和 n 的值, an 可以同通项公司计算出.
先假设 an = 1000 , 由 1000 = 3 + (n - 1)*3 求出 n = (1000-3)/3 +1 = 333.33333, 在对n 取整 n = 333
n = (int) ( ( ($x - a1)/d) +1 ) ;
可以知道 1000 以内有 333 个数是符合条件的.
在计算出 an = 3 + (333 - 1) * 3 = 999
所以得到数列 : 3, 6, 9 , 12 ... 999
在求和:
Sn = (a1 + an) * n/2 = (a1 + a1+(n-1)*d) * n / 2 = a1 * n + n*(n-1)*d/2
= a1 * (int) ( ( ($x - a1)/d) +1 ) + (int) ( ( ($x - a1)/d) +1 ) * ((int) ( ( ($x - a1)/d) +1 ) -1)*d/2
同理得到 1000 以内5的倍数的和,
3 和 5 求和中有重复的值累加了
是这些值:
15, 30, 45, 40
发现这些值是15的倍数 和上面一样可以求和
用前面求到的值相加再减去重复的和就可以解决我们的问题了.
毫无疑问这个算法可以完败循环。