数据结构基础(一)数组,矩阵
数据结构基础(一)
有一个等式,数据结构+算法=程序,说明了数据结构对于计算机程序设计的重要性。数据结构是指数据元素的集合(或数据对象)及元素间的相互关系和构造方法。数据对象中元素之间的相互关系称为数据的逻辑结构,数据元素及元素之间关系的存储形式称为存储结构(或物理结构)。
数据结构按照逻辑关系的不同,分为线性结构和非线性结构两种,线性结构又可分为树结构和图结构。
1.1 数组
1.数组的定义和基本运算
数组是程序中最常用的数据结构,数组的本质是内存中一段大小固定,地址连续的存储单元。
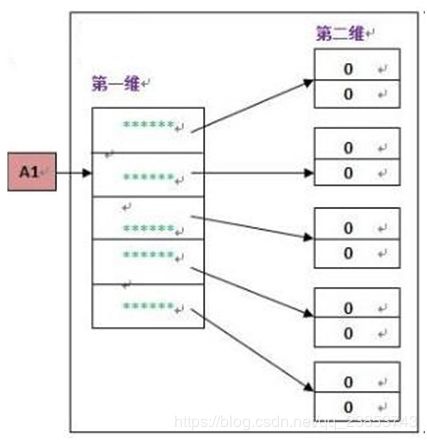
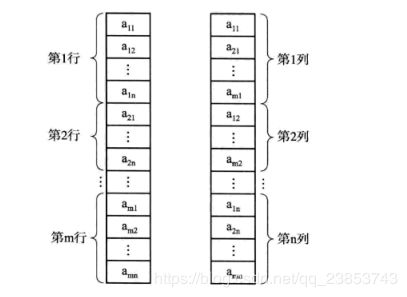
一维数组是一个长度固定,下标有序的线性序列。二位数组则是一个矩阵结构,本质上是以数组作为数组元素的数组,即“数组的数组”。以二维数组A[m,n]为例,其结构如图2-1所示:
A[m,n]可以看做一个行向量形式的线性序列:
Am,n =[[a11,a12…a1n],[ a21,a22…a2n],…,[ am1,am2…amn]];
也可以看做一个列向量形式的线性序列
Am,n =[[a11,a21…am1],[ a12,a22…am2],…,[ a1n,a2n…amn]];
二维数组的本质是一维数组的数组
数组的结构特点:
数组元素数目固定,一旦定义不可改变。
数组中的元素具有相同的类型。
数组下标具有上下界的约束且有序。
数组的两个基本运算:
给定一组下标,存取相应的数据元素。
给定一组下标,更改相应元素的值。
在程序设计语言中,把数组看做是具有共同名字的相同类型的多个变量的集合。
2. 数组元素的存储
数组适合采用顺序存储结构,对于数组一旦确定了其维数和各维的长度,便可分配存储空间。所以,只要给出一组下标便可求出相应数组元素的存储位置,在数组的顺序存储结构中,数组元素的位置和其下标呈线性关系。
二维数组的存储结构可分为以行为主存储和以列为主存储两种方式
设每个数组元素占用L个单元,m,n为数组的行数和列数,Loc(a11)表示元素a11的地址,
以行为主:
Loc(aij)=Loc(a11)+(i-1) ×n+(j-1) ×L
以列为主:
Loc(aij)=Loc(a11)+(j-1) ×m+(i-1) ×L
推广至多维数组,按下标顺序(以行为主)存储时,先排最右的下标,从右至左到最左下标,而逆下标顺序正好相反。
3.矩阵
在数学中,矩阵(Matrix)是一个按照长方阵列排列的复数或实数集合 [1] ,最早来自于方程组的系数及常数所构成的方阵。这一概念由19世纪英国数学家凯利首先提出。在数据结构中,主要讨论如何在节省存储空间的前提下,正确高效的运算矩阵。
在实际应用中,经常出现一些阶数很高的矩阵,同时在矩阵中有很多值相同的元素并且它们的分布有一定的规律——称为特殊矩阵(special matrix),对称矩阵就是其中一种。对称矩阵的特点是:在一个n阶方阵中,有aij=aji(1≤i,j≤n)。可以对这类矩阵进行压缩存储,从而节省存储空间,并使矩阵的各种运算能有效进行。
(1) 对称矩阵
对称矩阵关于主对角线对称,因此只需存储下三角部分(包括主对角线)即可。这样,原来需要存储n×n个存储单元,现在只需要n×(n+1)/2个存储单元,节约了大约一半的存储单元。当n较大时,这是比较可观的一部分存储单元。
如何只存储下三角部分的元素呢?由于下三角中共有n×(n+1)/2个元素,可将这些元素按行存储到一个数组SA[n(n+1)/2]中。这样,下三角中的元素aij(i≥j)存储到SA[k]中,在数组SA中的下标k和i、j的关系为:k=i×(i-1)/2+j-1,寻址的计算方法如图所示。
Java代码实现对称矩阵存储压缩:
package top.yxy.xs;
/**
* 稀疏矩阵的压缩存储
*
* 稀疏矩阵三元组顺序表
*
* 三元组顺序存储的稀疏矩阵类
*
* @author clarck
*
*/
public class SeqSparseMatrix {
// 矩阵行数、列数
private int rows, columns;
// 稀疏矩阵三元组顺序表
private SeqList list;
/**
* 构造rows行,colums列零矩阵
*
* @param rows
* @param columns
*/
public SeqSparseMatrix(int rows, int columns) {
if (rows <= 0 || columns <= 0)
throw new IllegalArgumentException("矩阵行数或列数为非正数");
this.rows = rows;
this.columns = columns;
// 构造空顺序表,执行SeqList()构造方法
this.list = new SeqList();
}
public SeqSparseMatrix(int rows, int columns, Triple[] elems) {
this(rows, columns);
// 按行主序插入一个元素的三元组
for (int i = 0; i < elems.length; i++)
this.set(elems[i]);
}
/**
* 返回矩阵第i行第j列元素,排序顺序表的顺序查找算法,O(n)
*
* @param i
* @param j
* @return
*/
public int get(int i, int j) {
if (i < 0 || i >= rows || j < 0 || j >= columns)
throw new IndexOutOfBoundsException("矩阵元素的行或列序号越界");
Triple item = new Triple(i, j, 0);
int k = 0;
Triple elem = this.list.get(k);
// 在排序顺序表list中顺序查找item对象
while (k < ((CharSequence) this.list).length() && item.compareTo(elem) >= 0) {
// 只比较三元组元素位置,即elem.row == i && elem.column == j
if (item.compareTo(elem) == 0)
return elem.value;
// 查找到(i, j), 返回矩阵元素
k++;
elem = ((Object) this.list).get(k);
}
return 0;
}
/**
* 以三元组设置矩阵元素
*
* @param elem
*/
public void set(Triple elem) {
this.set(elem.row, elem.colum, elem.value);
}
/**
* 设置矩阵第row行第column列的元素值为value,按行主序在排序顺序表list中更改或插入一个元素的三元组, O(n)
*
* @param row
* @param column
* @param value
*/
public void set(int row, int column, int value) {
// 不存储值为0元素
if (value == 0)
return;
if (row >= this.rows || column >= this.columns)
throw new IllegalArgumentException("三元组的行或列序号越界");
Triple elem = new Triple(row, column, value);
int i = 0;
// 在排序的三元组顺序表中查找elem对象,或更改或插入
while (i < this.list.length()) {
Triple item = this.list.get(i);
// 若elem存在,则更改改位置矩阵元素
if (elem.compareTo(item) == 0) {
// 设置顺序表第i个元素为elem
this.list.set(i, elem);
return;
}
// elem 较大时向后走
if (elem.compareTo(item) >= 0)
i++;
else
break;
}
this.list.insert(i, elem);
}
@Override
public String toString() {
String str = "三元组顺序表:" + this.list.toString() + "\n";
str += "稀疏矩阵" + this.getClass().getSimpleName() + "(" + rows + " * "
+ columns + "): \n";
int k = 0;
// 返回第k个元素,若k指定序号无效则返回null
Triple elem = this.list.get(k++);
for (int i = 0; i < this.rows; i++) {
for (int j = 0; j < this.columns; j++)
if (elem != null && i == elem.row && j == elem.colum) {
str += String.format("%4d", elem.value);
elem = this.list.get(k++);
} else {
str += String.format("%4d", 0);
}
str += "\n";
}
return str;
}
/**
* 返回当前矩阵与smat相加的矩阵, smatc=this+smat,不改变当前矩阵,算法同两个多项式相加
*
* @param smat
* @return
*/
public SeqSparseMatrix plus(SeqSparseMatrix smat) {
if (this.rows != smat.rows || this.columns != smat.columns)
throw new IllegalArgumentException("两个矩阵阶数不同,不能相加");
// 构造rows*columns零矩阵
SeqSparseMatrix smatc = new SeqSparseMatrix(this.rows, this.columns);
int i = 0, j = 0;
// 分别遍历两个矩阵的顺序表
while (i < this.list.length() && j < smat.list.length()) {
Triple elema = this.list.get(i);
Triple elemb = smat.list.get(j);
// 若两个三元组表示相同位置的矩阵元素,则对应元素值相加
if (elema.compareTo(elemb) == 0) {
// 相加结果不为零,则新建元素
if (elema.value + elemb.value != 0)
smatc.list.append(new Triple(elema.row, elema.colum,
elema.value + elemb.value));
i++;
j++;
} else if (elema.compareTo(elemb) < 0) { // 将较小三元组复制添加到smatc顺序表最后
// 复制elema元素执行Triple拷贝构造方法
smatc.list.append(new Triple(elema));
i++;
} else {
smatc.list.append(new Triple(elemb));
j++;
}
}
// 将当前矩阵顺序表的剩余三元组复制添加到smatc顺序表最后
while (i < this.list.length())
smatc.list.append(new Triple(this.list.get(i++)));
// 将smat中剩余三元组复制添加到smatc顺序表最后
while (j < smatc.list.length()) {
Triple elem = smat.list.get(j++);
if (elem != null) {
smatc.list.append(new Triple(elem));
}
}
return smatc;
}
/**
* 当前矩阵与smat矩阵相加,this+=smat, 改变当前矩阵,算法同两个多项式相加
*
* @param smat
*/
public void add(SeqSparseMatrix smat) {
if (this.rows != smat.rows || this.columns != smat.columns)
throw new IllegalArgumentException("两个矩阵阶数不同,不能相加");
int i = 0, j = 0;
// 将mat的各三元组依次插入(或相加)到当前矩阵三元组顺序表中
while (i < this.list.length() && j < smat.list.length()) {
Triple elema = this.list.get(i);
Triple elemb = smat.list.get(j);
// 若两个三元组表示相同位置的矩阵元素,则对应元素值相加
if (elema.compareTo(elemb) == 0) {
// 相加结果不为0,则新建元素
if (elema.value + elemb.value != 0)
this.list.set(i++, new Triple(elema.row, elema.colum,
elema.value + elemb.value));
else
this.list.remove(i);
j++;
} else if (elema.compareTo(elemb) < 0) { // 继续向后寻找elemb元素的插入元素
i++;
} else {
// 复制elemb元素插入作为this.list的第i个元素
this.list.insert(i++, new Triple(elemb));
j++;
}
}
// 将mat中剩余三元组依次复制插入当前矩阵三元组顺序表中
while (j < smat.list.length()) {
this.list.append(new Triple(smat.list.get(j++)));
}
}
// 深拷贝
public SeqSparseMatrix(SeqSparseMatrix smat) {
this(smat.rows, smat.columns);
// 创建空顺序表,默认容量
this.list = new SeqList();
// 复制smat中所有三元组对象
for (int i = 0; i < smat.list.length(); i++)
this.list.append(new Triple(smat.list.get(i)));
}
/**
* 比较两个矩阵是否相等
*/
public boolean equals(Object obj) {
if (this == obj)
return true;
if (!(obj instanceof SeqSparseMatrix))
return false;
SeqSparseMatrix smat = (SeqSparseMatrix) obj;
return this.rows == smat.rows && this.columns == smat.columns
&& this.list.equals(smat.list);
}
/**
* 返回转置矩阵
* @return
*/
public SeqSparseMatrix transpose() {
//构造零矩阵,指定行数和列数
SeqSparseMatrix trans = new SeqSparseMatrix(columns, rows);
for (int i = 0; i < this.list.length(); i++) {
//插入矩阵对称位置元素的三元组
trans.set(this.list.get(i).toSymmetry());
}
return trans;
}
} (2)稀疏矩阵
在矩阵中,若数值为0的元素数目远远多于非0元素的数目,并且非0元素分布没有规律时,则称该矩阵为稀疏矩阵。稀疏矩阵常使用三元组存储法,三元组表示法就是在存储非零元的同时,存储该元素所对应的行下标和列下标。稀疏矩阵中的每一个非零元素由一个三元组(i,j,aij)唯一确定。矩阵中所有非零元素存放在由三元组组成的数组中。
查看更多文章欢迎关注我的微信公众号:AlbertYang