算法分析——算法的渐进效率分析 和 渐进符号大O、大Ω、大θ、小o、小ω

上章 算法概述 中讲述了 在设计算法和比较算法时，设计人员更倾向于假设输入规模n无限大，然后再比较算法的渐进效率。

为什么要分析算法的渐进效率，而不是直接按照输入规模直接计算效率进行比较？

很直观的原因就是，当输入规模小的时候，各种算法间的差距并不会太大，对于大部分应用程序来讲，这些差距都可以被忽略。

现实原因是，要精确计算算法执行时所消耗的资源是非常繁琐，代价较大，甚至说不太切于实际的。

所以就有人发明了使用渐进分析法来分析算法的渐进效率。接下来的文章我们就将根据实际的例子进行具体的分析。

但在进行算法的渐进效率分析的时候，需要用到一些渐进符号，所以这里实现先对之后可能用到的渐进符号进行简单描述。

这地方可能有点比较难理解的是，渐进符号描述的表达式 表示 一个函数集合。而在渐进分析中的 ”=“更倾向于“∈ ”的意思。打个比方：渐进表达式 f(n) = O（g(n)）所表达的意思是，O(g(n)) = [ f(n),h(n).....g(n) ]; f(n) ∈ O(g(n))

一、大O表示法

      一般用于界定函数集合的上界，渐进表达式O（g（n））的含义就是，c为正常数，函数集合O中的元素的最大值不会超过c.g(n)。f(n) = O(g(n))的含义是，函数f(n)的属于集合O（g(n)）,因为函数集合O中的最大值为c.g(n)，所以f(n)的最大值为c.g(n)。由于只是渐进的上界，所以当函数g（n）的阶数越小时，上界越紧确。

      下面来看下 算法导论 中是如何描述大O表示法的。

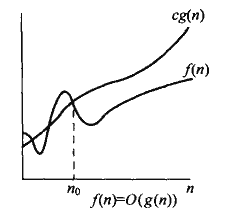
      当函数的大小只有上界，没有明确下界的时候，则可以使用大O表示法。f（n）= O（g（n））正式的数学定义：存在正常数c、n、n0，当n>n0的时，对于任意的f（n）对符合0<= f（n）<= c.g（n）。

      直观视觉图如下示：

                    

        该渐进描述符一般用与描述算法的最坏复杂度。读者可以在这地方思考下，为什么用大Ω来描述算法的最坏复杂度没有意义（大Ω描述的界是渐进最小，当用大Ω来描述最坏复杂度时，因为这只是一个下界，并不能说明算法的最坏复杂度，所以没意义）。

二、大Ω表示法

      一般用于界定函数集合的下界，渐进表达式Ω（g（n））的含义就是，函数集合Ω中的元素的最小值不会低于c.g(n)。f(n) = Ω（g（n））的含义是，函数f(n)的属于集合Ω（g（n））,因为函数集合Ω中的最小值为c.g(n)，所以f(n)的最小值为c.g(n)。

     算法导论 中是如何描述大Ω表示法的。     

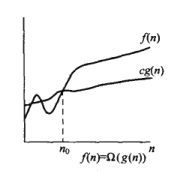
     当函数的大小只有下界，没有明确的上界的时候，可以使用大Ω表示法。f（n）= Ω（g（n））正式的数学定义：存在正常数c、n、n0，当n>n0的时，对于任意的f（n）对符合0<= c.g（n）<= f（n）。

     直观视觉图如下所示：

                    

    该渐进描述符一般用与描述算法的最优复杂度。读者可以在这地方思考下，为什么用大O来描述算法的最优复杂度没有意义（因为大O描述的界时渐进最大的，当你说你的算法最快为O(f(n))的时候，因为函数描述的只是个上界，并无法描述最小值，所以没意义）。

三、大θ表示法

       用于界定函数的渐进上界和渐进下界。当f（n）= θ（g（n））的时候，代表着g（n）为f（n）的渐进紧确界。而θ渐进描述符在所有的渐进描述符中是最严格的一个，因为它既描述了函数的上界，有描述了函数的下界。

       算法导论 中是如何描述大θ表示法的。

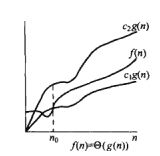
       f（n）= θ（c.g（n））正式的数学定义：存在正常数c1、c2、n、n0，当n>n0的时，对于任意的f（n）对符合c1.g（n）<= f（n）<= c2.g（n），c1.g（n）、c2.g（n）都是渐进正函数（当n趋于无穷大的时候，f（n）为正）。  

        直观视觉图如下所示：              

                    

算法导论中还根据大O，大Ω，大θ的定义得到一个定理：

当且仅当函数f（n）= O（g（n））and f（n）=Ω（g（n））时，f（n）= θ（g（n））

四、小o表示法

       刚才我们介绍了大O表示法，大O表示法所描述的界，可以是渐进紧确的，也可以是非渐进紧确的。而小o表示法所描述的界是非渐进紧确的。下面我们看下小o表示法的数学定义：

     函数f（n）= o（g（n））对于任意的正常数c，存在常数n0 > 0，使得对所有的n > n0 都存在0 <= f（n）<= c.g（n）。

      这里可以根据定义看出同样是0 <= f（n）<= c.g（n），大O表示法是存在一个常数c符合该条件，而小o表示法是对于所有的正常数c都符合该条件。所以当n趋于无穷大，c也趋于无穷大的时候，小o表示法描述的界的宽松范围比大O表示法描述的界宽松范围大最少一个次方，所以小o表示法所描述的界必然是渐进非紧确的。

五、小ω表示法

       小ω表示法和大Ω表示法的区别和小o表示法和大O表示法的区别类似。其描述的界也是渐进非紧确的。下面是小o表示法的数学定义：

     函数f（n）= o（g（n））对于任意的正常数c，存在常数n0 > 0，使得对所有的n > n0 都存在0 <= c.g（n）<=  f（n）。

函数间的特性和比较

        在后续的实际算法分析中，会经常使用到以上五种描述符，这里也说一下它们之间的比较关系和特性，方便以后做分析时，理解公式的推演过程。

       传递性：

                f(n) = θ(g(n))  和 g(n) =  θ(h(n))   可以得出 f(n) =   θ(h(n))

                f(n) = O(g(n))  和 g(n) = O(h(n))   可以得出 f(n) =  O(h(n))

                f(n) = Ω(g(n))  和 g(n) = Ω(h(n))   可以得出 f(n) =  Ω(h(n))

                f(n) = o(g(n))  和  g(n) =  o(h(n))   可以得出 f(n) =  o(h(n))

                f(n) = ω(g(n))  和 g(n) = ω(h(n))   可以得出 f(n) =  ω(h(n))

       自反性： 

                f(n) = θ(f(n))     可以得出  f(n) = O(f(n))   和  f(n) = Ω(f(n))

       对称性：

                f(n) = Θ(g(n))   当且仅当 g(n) = Θ(f(n))

       转置对称性：

                f(n) = O(g(n))   当且仅当 g(n) = Ω(f(n))

                f(n) = o(g(n))   当且仅当 g(n) = ω(f(n))

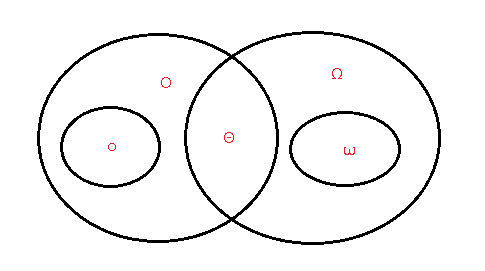
下面是关于这五种渐进符号在视觉上的直观的比较关系：

        

除了这些渐进符号之外，还有一些标准记号和常用符号在算法分析中也有遇到，不过因为其相对渐进符号来讲，比较易懂，这里就不一一赘述了，如果大家感兴趣可以去 算法导论的3.2章节自行了解下。这里也说一下，个人感觉渐进符号在算法分析的基础中还是比较重要的一块基础知识，建议基础较差的同学可以多看看其他的资料（书籍，帖子），自己多总结思考下，相信很快就可以掌握其中的奥秘