Skip-Thought Vector —— 跳跃思维句表示
目录
- 《Skip-Though Vector》 —— 跳跃思维句表示
- 1、句表示简介
- 1.1 基于词袋模型的句表示
- 1.1.1 词袋模型
- 1.1.2 词表示加权 -> 句表示
- 1.2 基于神经网络的句表示
- 1.2.1 语言模型
- 1.2.2 doc2vec
- 1.2.3 基于复述句匹配的句表示
- 2、论文动机
- 2.1 Skip-gram模型
- 3、Skip-Thought模型
- 3.1 Skip-Thought具体原理
- 3.2 Skip-Thought模型损失函数
- 3.3 未登录词处理
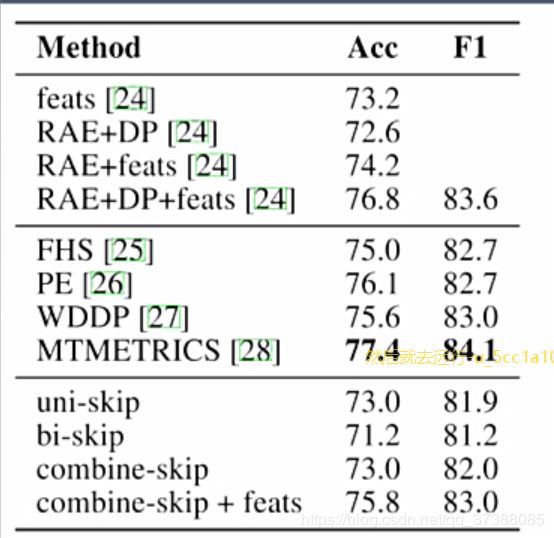
- 4、实验结果
- 4.1 语义相似性度量:两个句子的语义相似性计算(余弦相似度)
- 4.2 复述句检测:判断两个句子是否语义一致(二分类)
- 4.3 句子分类:判断句子属于哪个类别
- 5、后续改进
- 5.1 Quick Thought
- 6、总结
- 6.1 论文主要创新点
《Skip-Though Vector》 —— 跳跃思维句表示
作者:Ryan Kiros
单位:University of Toronto
发表会议及时间:NIPS 2015
1、句表示简介
神经网络模型生成的词表示被称为词向量,这是一个低维的向量表示,已经成为了当前工业界和学术界的通用文本表示方法。在自然语言处理领域,有着很多句子级别的任务,例如情感分析、句对匹配等。毫无疑问,句子级别的建模能够更为有效地改善这些任务的处理性能。
通过某种方式将句子编码为计算机可以处理的形式(向量),实现一次表示,多领域应用,是自然语言表示总的重要任务。

句表示研究意义
一次表示,多领域应用,以及预先训练,应用微调已经成为了工业界解决具体NLP任务的最佳思路,因为其可以充分利用无监督的数据来辅助有监督任务学习语言信息,往往也能取得很好的效果。
两种应用思路:句表示训练完毕后不再调整,只在具体任务上训练分类器;或者句表示的编码模型也随着下游任务进行训练,如Bert。
句表示发展历史
趋势:让句子的语义更“准确”地编码到有限维的向量中,在向量子空间中保持句子的语义关系,更好地利用语言模型以及无监督上下文信息;
1.1 基于词袋模型的句表示
1.1.1 词袋模型
One-hot编码,又称为独热编码,其方法是使用N位状态寄存器来对N个状态进行编码,每个状态都有其独立的寄存器位,并且在任意时候,其中只有一位有效,One-hot在特征提取上属于词袋模型(bag of words)。关于如何使用one-hot抽取文本特征向量我们通过以下例子来说明,假设语料库中有三段话:

1.1.2 词表示加权 -> 句表示
另一种基于词袋模型的方法是将词向量进行加权得到稠密的句表示,词向量的加权方式一般遵循一个准则,越常见的词权重越小,这里简单介绍两种:
(1)TF-IDF算法
TF-IDF算法(Term Frequency-Inverse Document Frequency,词频-逆文档频次算法)是一种基于统计的计算方法,常用于评估在一个文档集中一个词对某份文档的重要程度。
从算法的名称就可以看出,TF-IDF算法由两部分组成:TF算法及IDF算法。
TF算法是统计一个词在一篇文档中出现的频次,其基本思想是,一个词在文档中出现的次数越多,则其对文档的表达能力也就越强。
IDF算法是统计一个词在文档集的多少个文档中出现,其基本思想是,如果一个词在越少的文档中出现,则其对文档的区分能力也就越强。
TF算法和IDF算法也能单独使用,但是在使用过程中发现这两种算法都有其不足之处。TF算法仅衡量词的出现频次,但是没有考虑到词对文档的区分能力。
比如下面这篇文档:
世界献血日,学校团体、献血服务志愿者等可到血液中心参观检验加工过程,我们会对检验结果进行公示,同时血液的价格也将进行公示。
上文中“献血”“血液”“进行”“公示”等词出现的频次为2,如果从TF算法的角度,它们对于这篇文档的重要性是一样的。但是实际上明显“血液”“献血”对这篇文档来说更关键。而IDF则是相反,强调的是词的区分能力,但是一个词既然能在一篇文档中频繁出现,那说明这个词能够很好地表现这篇文档的特征,忽略这一点显然也是不合理的,于是,学者们将这两种算法综合进行使用,构成TF-IDF算法,从词频、逆文档频次两个角度对词的重要性进行衡量。
在实际使用中,TF的计算公式如下所示: t f i j = n i j ∑ k n i j tf_{ij}=\frac{n_{ij}}{\sum_kn_{ij}} tfij=∑knijnij
公式中的 n i j n_{ij} nij表示词i在文档j中的出现频次,但是仅用频次来表示,长文本中的词出现频次高的概率会更大,这一点会影响到不同文档之间关键词权值的比较。所以在计算过程中一般会对词频进行归一化。分母部分就是统计文档中每个词出现次数的总和,也就是文档的总次数。
以上文文档为例,“献血”一次出现次数为2,文档的总词数为30,则: t f ( 献 血 ) = n ( 献 血 ) / n ( 总 ) = 2 / 30 ≈ 0.067 tf(献血)=n(献血)/n(总)=2/30\approx 0.067 tf(献血)=n(献血)/n(总)=2/30≈0.067
更直白的表示方式就是: t f ( w o r d ) = ( w o r d 在 文 档 中 出 现 的 次 数 ) / ( 文 档 总 次 数 ) tf(word)=(word在文档中出现的次数)/(文档总次数) tf(word)=(word在文档中出现的次数)/(文档总次数)
而IDF的计算常用式为: i d f i = l o g ( ∣ D ∣ 1 + ∣ D i ∣ ) idf_i = log(\frac{|D|}{1+|D_i|}) idfi=log(1+∣Di∣∣D∣)
∣ D ∣ |D| ∣D∣为文档集中总文档数, ∣ D i ∣ |D_i| ∣Di∣为文档集中出现词i的文档数量。分母加1是采用了拉普拉斯平滑,避免有部分新的词没有在语料库中出现过而导致分母为零的情况出现,增强算法的健壮性。
TF-IDF算法就是TF算法和IDF算法的综合使用,具体计算方法如下所示: t f − i d f ( i , j ) = t f i j ∗ i d f i = n i j ∑ k n i j ∗ l o g ( ∣ D ∣ 1 + ∣ D i ∣ ) tf-idf(i,j)=tf_{ij}*idf_{i}=\frac{n_{ij}}{\sum_kn_{ij}}*log(\frac{|D|}{1+|D_i|}) tf−idf(i,j)=tfij∗idfi=∑knijnij∗log(1+∣Di∣∣D∣)
以上文文档为例,经过计算得到“献血”“血液”“进行”“公示”四个词出现的频次均为2,因此它们的tf值都是0.067。现在假设我们具有的文档集有1000篇文档,其中出现“献血”“血液”“进行”“公示”的文档数分别为10、15、100、50,则根据上述TF-IDF计算公式可以得到每个词的tf-idf值。
(2)SIF算法
SIF算法仅仅考虑TF,其计算公式如下: S I F ( x ) = α T F ( x ) + α SIF(x)=\frac{\alpha}{TF(x)+\alpha} SIF(x)=TF(x)+αα
这种方法的优点是简单快捷,缺点是没有考虑语序,没有合理地利用句子语义信息;
1.2 基于神经网络的句表示
1.2.1 语言模型
- Sentence 1:美联储主席本·伯南克昨天告诉媒体7000亿元的救助资金;
- Sentence 2:美主席联储本·伯南克告诉昨天媒体7000亿元的资金救助;
以上哪一个句子更像一个合理的句子?如何量化评估?
使用语言模型: P ( S ) = P ( w 1 , w 2 , ⋯ , w n ) = P ( w 1 ) P ( w 2 ∣ w 1 ) P ( w 3 ∣ w 1 , w 2 ) ⋯ P ( w n ∣ w 1 , w 2 , ⋯ , w n − 1 ) P(S)=P\left(w_{1}, w_{2}, \cdots, w_{n}\right)=P\left(w_{1}\right) P\left(w_{2} \mid w_{1}\right) P\left(w_{3} \mid w_{1}, w_{2}\right) \cdots P\left(w_{n} \mid w_{1}, w_{2}, \cdots, w_{n-1}\right) P(S)=P(w1,w2,⋯,wn)=P(w1)P(w2∣w1)P(w3∣w1,w2)⋯P(wn∣w1,w2,⋯,wn−1)
量化评估: L = ∑ w ∈ C log P ( w ∣ context ( w ) ) L=\sum_{w \in C} \log P(w \mid \operatorname{context}(w)) L=w∈C∑logP(w∣context(w))
1.2.2 doc2vec
doc2vec利用的就是语言模型,doc2vec在模型中加入了段落ID或者句子ID,如果语料中有K个句子,该模型就会随机初始化一个 K ∗ D K*D K∗D的矩阵,D表示要训练的句子的维度,训练完成后就得到了句子表示的向量。
这种方法的优点是能够充分利用语言模型,但是该模型没有考虑到句子之间的信息。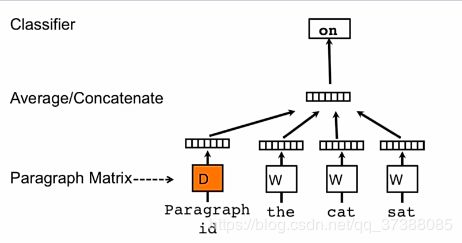
1.2.3 基于复述句匹配的句表示
- Sentence 1:小王是老王的儿子;
- Sentence 2:老王是小王的爸爸;
上述两个句子互为复述句,应该语义接近(句表示近似)。
衡量指标为: 1 ∣ S ∣ ( ∑ < s 1 , s 2 > ∈ S max ( 0 , δ − cos ( g ( s 1 ) , g ( s 2 ) ) + − cos ( g ( s 1 ) , g ( t 1 ) ) ) + max ( 0 , δ − cos ( g ( s 1 ) , g ( s 2 ) ) + − cos ( g ( s 2 ) , g ( t 2 ) ) ) ) \frac{1}{|S|}(\sum_{
测试数据集包括情感分类、主题分类、语义相似度度量、复述句检测、文本蕴含等;
测试方法为:固定句表示,在对应任务等训练数据集上学习分类器;
两类方法对比:
基于语言模型的句表示:利用了无监督文本语料,利用了词与词共现信息,可大规模训练;
- 优点:利用无监督语料,成本低;语言模型学习语言知识;
- 缺点:句子之间隐藏的语义联系;学习句表示,忽略句子间的信息是极为不合理的;
基于复述句对的句表示方法:语料可通过机器翻译大规模获得;建模句对关系;
- 优点:建模了句对之间的相似与不相似关系;
- 缺点:仅仅建模了相关性,忽略了句子间复杂的语义关系;
Skip-thought的目的是利用大规模无监督语料建模句子间的关系
2、论文动机
在词向量表征中,我们可以由一个词的上下文了解词的语义信息,我们把这一个定理推广到句子级别是否也成立呢?
假设语料库中有一段话:
- 自然语言处理是计算机科学领域与人工智能领域中的一个重要方向;
- 它研究能实现人与计算机之间用自然语言进行有效通信的各种理论和方法;
- 自然语言处理是一门融语言学、计算机科学、数学于一体的科学。
在一段话中,句子与其上下句总是存在某些语义联系的,能否通过一个句子预测出其上下文的句子?
先回顾一下Skip-gram模型。
2.1 Skip-gram模型
Skip-gram模型是通过中心词预测背景词,如下图所示,通过中心词learning预测其上下文两个背景词。
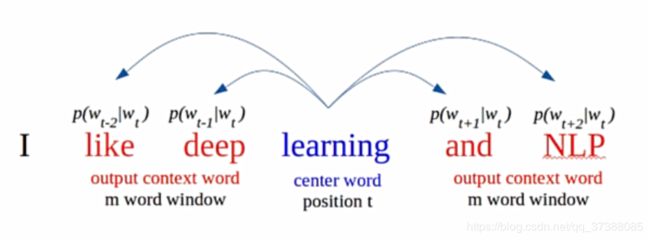

其损失函数和概率计算公式如下所示: L = − 1 T ∑ t = 1 T ∑ − m ≤ j ≤ m , j ≠ 0 log p ( w t + j ∣ w t ) L=-\frac{1}{T} \sum_{t=1}^{T} \sum_{-m \leq j \leq m,j \neq 0} \log p\left(w_{t+j} \mid w_{t}\right) L=−T1t=1∑T−m≤j≤m,j=0∑logp(wt+j∣wt) p ( w t + j ∣ w t ) = exp ( v w t T v w t + j ) ∑ i = 1 ⌈ V ∣ exp ( v w t T v w i ) p\left(w_{t+j} \mid w_{t}\right)=\frac{\exp \left(\mathbf{v}_{w_{t}}^{\mathrm{T}} \mathbf{v}_{w_{t+j}}\right)}{\sum_{i=1}^{\lceil V \mid} \exp \left(\mathbf{v}_{w_{t}}^{\mathrm{T}} \mathbf{v}_{w_{i}}\right)} p(wt+j∣wt)=∑i=1⌈V∣exp(vwtTvwi)exp(vwtTvwt+j)
Skip-gram的思想能否迁移到句子级别?
3、Skip-Thought模型
3.1 Skip-Thought具体原理
给定一个句子"I could see the cat on the steps",其对应的上一句话为"I got back home",其下一句话为"This was strange"。
Skip-Though模型希望通过编码中间的句子来预测其前一个句子和后一个句子,前一个句子和后一个句子分别用不同的解码器进行解码,也就是根据中间句子的句向量表示进行自回归的Decoder把句子解码出来,这借鉴了机器翻译中的思想。
使用两个独立的Decoder分别建模前一句和后一句是为了用独立的语义去编码前一句和后一句。
Skip-Thought模型的编码器部分使用GRU进行Encoder,GRU中有更新门和重置门,更新门对应 z t z^t zt,重置门对应 r t r^t rt。更新门用于控制前一个时刻的信息被带入当前时刻的程度,更新门的值越大,说明前一时刻的信息带入当前时刻越多。重置门控制的是前一时刻有多少信息被写入到当前时刻的候选集。GRU主要的公式如下所示: r t = σ ( W r x t + U r h t − 1 ) \mathbf{r}^{t}=\sigma\left(\mathbf{W}_{r} \mathbf{x}^{t}+\mathbf{U}_{r} \mathbf{h}^{t-1}\right) rt=σ(Wrxt+Urht−1) z t = σ ( W z x t + U z h t − 1 ) \mathbf{z}^{t}=\sigma\left(\mathbf{W}_{z} \mathbf{x}^{t}+\mathbf{U}_{z} \mathbf{h}^{t-1}\right) zt=σ(Wzxt+Uzht−1) h ‾ t = tanh ( W x t + U ( r t ⊙ h t − 1 ) ) \overline{\mathbf{h}}^{t}=\tanh \left(\mathbf{W} \mathbf{x}^{t}+\mathbf{U}\left(\mathbf{r}^{t} \odot \mathbf{h}^{t-1}\right)\right) ht=tanh(Wxt+U(rt⊙ht−1)) h t = ( 1 − z t ) ⊙ h t − 1 + z t ⊙ h ‾ t \mathbf{h}^{t}=\left(1-\mathbf{z}^{t}\right) \odot \mathbf{h}^{t-1}+\mathbf{z}^{t} \odot \overline{\mathbf{h}}^{t} ht=(1−zt)⊙ht−1+zt⊙ht
接下来讲解一下Skip-Thought部分的解码器,Decoder部分使用的同样是GRU,Decoder部分的GRU是带有条件信息的,也就是编码器得到的中间句子的编码信息 h i h_i hi,从而使得Encoder部分的GRU每次都能携带中间句子的信息做出决策。
Skip-Thought解码器部分的计算公式为: r t = σ ( W r d x t − 1 + U r d h t − 1 + C r h i ) \mathbf{r}^{t}=\sigma\left(\mathbf{W}_{r}^{d} \mathbf{x}^{t-1}+\mathbf{U}_{r}^{d} \mathbf{h}^{t-1}+\mathbf{C}_{r} \mathbf{h}_{i}\right) rt=σ(Wrdxt−1+Urdht−1+Crhi) z t = σ ( W z d x t − 1 + U z d h t − 1 + C z h i ) \mathbf{z}^{t}=\sigma\left(\mathbf{W}_{z}^{d} \mathbf{x}^{t-1}+\mathbf{U}_{z}^{d} \mathbf{h}^{t-1}+\mathbf{C}_{z} \mathbf{h}_{i}\right) zt=σ(Wzdxt−1+Uzdht−1+Czhi) h ‾ t = tanh ( W d x t + U d ( r t ⊙ h t − 1 ) + C h i ) \overline{\mathbf{h}}^{t}=\tanh \left(\mathbf{W}^{d} \mathbf{x}^{t}+\mathbf{U}^{d}\left(\mathbf{r}^{t} \odot \mathbf{h}^{t-1}\right)+\mathbf{C h}_{i}\right) ht=tanh(Wdxt+Ud(rt⊙ht−1)+Chi) h i + 1 t = ( 1 − z t ) ⊙ h t − 1 + z t ⊙ h ‾ t \mathbf{h}_{i+1}^{t}=\left(1-\mathbf{z}^{t}\right) \odot \mathbf{h}^{t-1}+\mathbf{z}^{t} \odot \overline{\mathbf{h}}^{t} hi+1t=(1−zt)⊙ht−1+zt⊙ht
3.2 Skip-Thought模型损失函数
Skip-Thought模型的思想是给定中心句预测其上一个句子和下一个句子,所以只需要给定一段(三句)文本( s i − 1 , s i , s i + 1 s_{i-1},s_i,s_{i+1} si−1,si,si+1),因此可以用两个函数建模损失函数: ∑ t log P ( w i + 1 t ∣ w i + 1 < t , h i ) + ∑ t f log P ( w i − 1 t ∣ w i − 1 < t , h i ) \sum_{t} \log P\left(w_{i+1}^{t} \mid w_{i+1}^{
损失函数的意义是首先对中心句进行编码得到 h i h_i hi,然后由 h i h_i hi进行损失函数的计算;
模型将训练集的所有句子组合加入训练,在测试时将句子所有单词的 embedding 输入到 encoder 即可得到句子的 embedding 。
3.3 未登录词处理
如果测试时某些单词未在训练时见过(未登录词),则可以通过一些广义词向量来解决。如:假设 V w 2 v V_{w2v} Vw2v为更大规模的、通过 word2vec 训练得到的词向量, V r n n V_{rnn} Vrnn 为本模型训练得到的词向量。我们学习线性映射 f : V w 2 v → V r n n f:V_{w2v}\rightarrow V_{rnn} f:Vw2v→Vrnn,然后对于模型的未登录词 w u w_u wu,得到模型的词向量 x → u r n n = f ( x → u w 2 v ) \overrightarrow{\mathbf{x}}_{u}^{r n n}=f\left(\overrightarrow{\mathbf{x}}_{u}^{w 2 v}\right) xurnn=f(xuw2v):
4、实验结果
4.1 语义相似性度量:两个句子的语义相似性计算(余弦相似度)
4.2 复述句检测:判断两个句子是否语义一致(二分类)
4.3 句子分类:判断句子属于哪个类别
5、后续改进
5.1 Quick Thought
论文《An efficient framework for learning sentence representations》 提出了一种新的sentence vector 方式Quick thought Vector,相比较《Skip-Thought Vectors》 而言它的训练速度更快。

Quick thought Vector 通过分类器来区分句子的前后句和其它句子,模型结构如上图所示。这将生成问题视为从所有可能的句子中选择一个句子,因此可以看作是对生成问题的判别近似。
设句子 s i = { w i ( 1 ) , w i ( 2 ) , ⋯ , w i ( τ i ) } \mathbf{s}_{i}=\left\{w_{i}^{(1)}, w_{i}^{(2)}, \cdots, w_{i}^{\left(\tau_{i}\right)}\right\} si={wi(1),wi(2),⋯,wi(τi)}, τ i \tau_{i} τi为句子长度。 w i t w_i^{t} wit为句子 s i s_i si的第t个单词。
令句子 s i s_i si附近窗口大小d的句子集合为 S i , c t x S_{i,ctx} Si,ctx、句子 s i s_i si的候选样本句子集合为 S i , c a n d S_{i,cand} Si,cand,其中满足 S i , c t x ⊂ S i , c a n d \mathcal{S}_{i, c t x} \subset \mathcal{S}_{i, c a n d} Si,ctx⊂Si,cand。即: S i , c a n d S_{i,cand} Si,cand不仅包含了句子 s i s_i si附近的句子,也包含了很多其它句子。
使用编码器 f对 s i s_i si编码、编码器 g对候选句子 s i , cand ∈ S i , cand \mathbf{s}_{i, \text {cand}} \in \mathcal{S}_{i, \text {cand}} si,cand∈Si,cand编码,模型预测候选句子\mathbf{s}{i, c a n d} \in \mathcal{S}{i, c t x}的概率: p ( s i , c a n d ∣ s i , S i , c a n d ) = exp [ c ( f ( s i ) , g ( s i , c a n d ) ) ] ∑ s ′ ∈ S i , c a n d exp [ c ( f ( s i ) , g ( s ′ ) ] p\left(\mathbf{s}_{i, c a n d} \mid \mathbf{s}_{i}, \mathcal{S}_{i, c a n d}\right)=\frac{\exp \left[c\left(f\left(\mathbf{s}_{i}\right), g\left(\mathbf{s}_{i, c a n d}\right)\right)\right]}{\sum_{\mathbf{s}^{\prime} \in \mathcal{S}_{i, c a n d}} \exp \left[c\left(f\left(\mathbf{s}_{i}\right), g\left(\mathbf{s}^{\prime}\right)\right]\right.} p(si,cand∣si,Si,cand)=∑s′∈Si,candexp[c(f(si),g(s′)]exp[c(f(si),g(si,cand))]
- 上述公式中的 c ( ⋅ , ⋅ ) c(·,·) c(⋅,⋅)为一个打分函数(或者分类器),在论文中 c ( u → , v → ) c(\overrightarrow{\mathbf{u}}, \overrightarrow{\mathbf{v}}) c(u,v)简单定义为 c ( u → , v → ) = u → ⋅ v → c(\overrightarrow{\mathbf{u}}, \overrightarrow{\mathbf{v}})=\overrightarrow{\mathbf{u}} \cdot \overrightarrow{\mathbf{v}} c(u,v)=u⋅v。如此简单的分类器是为了迫使编码器能够学习到更加丰富的句子表示;
- 编码器f和f使用不同的参数,这是借鉴了word2vec的结构:中心词通过 W W W编码(输入向量)、目标词经过 W ′ W' W′映射(输出向量),两者点积得到得分;
- 在测试时给定句子 s t e s t s_{test} stest,其表示是两个编码器输出的拼接: f ( s test ) : g ( s test ) f\left(\mathbf{s}_{\text {test}}\right): g\left(\mathbf{s}_{\text {test}}\right) f(stest):g(stest);
6、总结
6.1 论文主要创新点
- 提出了一种新的句表示方法——考虑了句子间的关系,利用了无监督语料;
- 证明了一次训练多次使用的可行性;
- 对后续工作有很大的启发——实验分析十分详尽;