1013 Battle Over Cities（连通分量个数，dfs）

参考博客：https://blog.csdn.net/qq_33913037/article/details/71213985?locationNum=1&fps=1
https://www.liuchuo.net/archives/2346
1013 Battle Over Cities（25 分）

It is vitally important to have all the cities connected by highways in a war. If a city is occupied by the enemy, all the highways from/toward that city are closed. We must know immediately if we need to repair any other highways to keep the rest of the cities connected. Given the map of cities which have all the remaining highways marked, you are supposed to tell the number of highways need to be repaired, quickly.

For example, if we have 3 cities and 2 highways connecting city​1​​-city​2​​ and city​1​​-city​3​​. Then if city​1​​ is occupied by the enemy, we must have 1 highway repaired, that is the highway city​2​​-city​3​​.
Input Specification:

Each input file contains one test case. Each case starts with a line containing 3 numbers N (<1000), M and K, which are the total number of cities, the number of remaining highways, and the number of cities to be checked, respectively. Then M lines follow, each describes a highway by 2 integers, which are the numbers of the cities the highway connects. The cities are numbered from 1 to N. Finally there is a line containing K numbers, which represent the cities we concern.
Output Specification:

For each of the K cities, output in a line the number of highways need to be repaired if that city is lost.
Sample Input:

3 2 3
1 2
1 3
1 2 3

Sample Output:

1
0
0

题目大意：给出n个城市之间有相互连接的m条道路，当删除一个城市和其连接的道路的时候，问其他几个剩余的城市至少要添加多少个路线才能让它们重新变为连通图。

先解释几个名词：
连通图和连通分量

1．顶点间的连通性
　 在无向图G中，若从顶点vi到顶点vj有路径(当然从vj到vi也一定有路径)，则称vi和vj是连通的。

2．连通图
　若V(G)中任意两个不同的顶点vi和vj都连通(即有路径)，则称G为连通图(Con-nected Graph)。
　
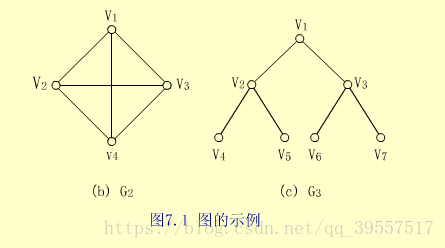
【例】图G2，和G3是连通图。

3．连通分量
　无向图G的极大连通子图称为G的最强连通分量(Connected Component)。
注意：
　　① 任何连通图的连通分量只有一个，即是其自身
　② 非连通的无向图有多个连通分量。
　
【例】下图中的G4是非连通图，它有两个连通分量H1和H2。

强连通图和强连通分量

1．强连通图
　 有向图G中，若对于V(G)中任意两个不同的顶点vi和vj，都存在从vi到vj以及从vj到vi的路径，则称G是强连通图。

2．强连通分量
　有向图的极大强连通子图称为G的强连通分量。
注意：
　① 强连通图只有一个强连通分量，即是其自身。

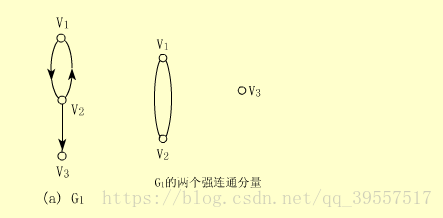
【例】下图中的G1不是强连通图，因为v3到v2没有路径，但它有两个强连通分量，如右图所示。

分析：添加的最少的路线，就是他们的连通分量数-1，因为当a个互相分立的连通分量需要变为连通图的时候，只需要添加a-1个路线，就能让他们相连。所以这道题就是求去除了某个结点之后其他的图所拥有的连通分量数。

使用邻接矩阵存储，对于每一个被占领的城市，去除这个城市结点，就是把它标记为已经访问过，这样在深度优先遍历的时候，对于所有未访问的结点进行遍历，就能求到所有的连通分量的个数～记得因为有很多个要判断的数据，每一次输入被占领的城市之前要把visit数组置为false～～

#include 
#include 
using namespace std;
int v[1010][1010];
bool visit[1010];
int n;
void dfs(int node){
    visit[node] = true;
    for(int i = 1; i <= n; i++){
        if(visit[i] == false && v[node][i] == 1)
            dfs(i);
    }
}
int main(){
    int m, k, a, b;
    scanf("%d%d%d", &n, &m, &k);
    for(int i = 0; i < m; i++){
        scanf("%d%d", &a, &b);
        v[a][b] = v[b][a] = 1;
    }
    for(int i = 0; i < k; i++) {
        fill(visit, visit + 1010, false);
        scanf("%d", &a);
        int cnt = 0;
        visit[a] = true;
        for(int j = 1; j <= n; j++){
            if(visit[j] == false){
                dfs(j);
                cnt++;
            }
        }
        printf("%d\n", cnt - 1);
    }
    return 0;
}